|
Nesbitt's Inequality
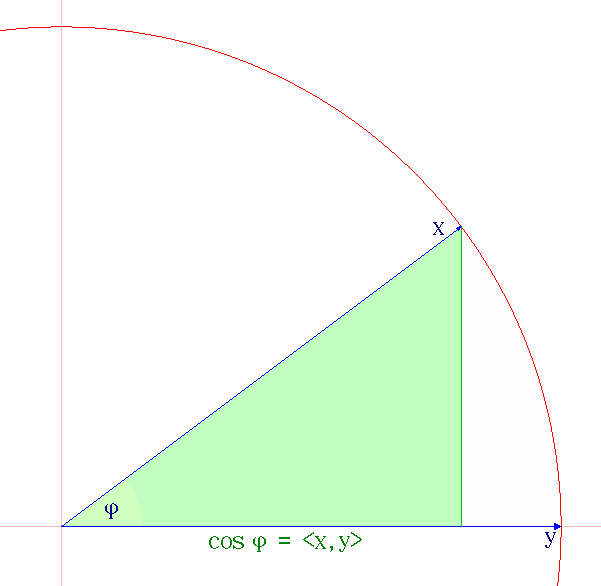
In mathematics, Nesbitt's inequality (mathematics), inequality states that for positive real numbers ''a'', ''b'' and ''c'', :\frac+\frac+\frac\geq\frac. It is an elementary special case (N = 3) of the difficult and much studied Shapiro inequality, and was published at least 50 years earlier. There is no corresponding upper bound as any of the 3 fractions in the inequality can be made arbitrarily large. Proof First proof: AM-HM inequality By the Arithmetic mean, AM-Harmonic mean, HM inequality on (a+b),(b+c),(c+a), :\frac\geq\frac. Clearing denominators yields :((a+b)+(a+c)+(b+c))\left(\frac+\frac+\frac\right)\geq 9, from which we obtain :2\frac+2\frac+2\frac\geq9 by expanding the product and collecting like denominators. This then simplifies directly to the final result. Second proof: Rearrangement Suppose a \ge b \ge c , we have that :\frac 1 \ge \frac 1 \ge \frac 1 define :\vec x = (a, b, c) :\vec y = \left(\frac 1 , \frac 1 , \frac 1 \right) The scalar product of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequality (mathematics)
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities: * The notation ''a'' ''b'' means that ''a'' is greater than ''b''. In either case, ''a'' is not equal to ''b''. These relations are known as strict inequalities, meaning that ''a'' is strictly less than or strictly greater than ''b''. Equivalence is excluded. In contrast to strict inequalities, there are two types of inequality relations that are not strict: * The notation ''a'' ≤ ''b'' or ''a'' ⩽ ''b'' means that ''a'' is less than or equal to ''b'' (or, equivalently, at most ''b'', or not greater than ''b''). * The notation ''a'' ≥ ''b'' or ''a'' ⩾ ''b'' means that ''a'' is greater than or equal to ''b'' (or, equivalently, at least ''b'', or not less than ''b''). The re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shapiro Inequality
In mathematics, the Shapiro inequality is an inequality (mathematics), inequality proposed by Harold S. Shapiro in 1954. Statement of the inequality Suppose n is a natural number and x_1, x_2, \dots, x_n are positive numbers and: * n is even and less than or equal to 12, or * n is odd and less than or equal to 23. Then the Shapiro inequality states that :\sum_^ \frac \geq \frac where x_=x_1, x_=x_2. For greater values of n the inequality does not hold and the strict lower bound is \gamma \frac with \gamma \approx 0.9891\dots. The initial proofs of the inequality in the pivotal cases n=12 (Godunova and Levin, 1976) and n=23 (Troesch, 1989) rely on numerical computations. In 2002, P.J. Bushell and J.B. McLeod published an analytical proof for n=12. The value of \gamma was determined in 1971 by Vladimir Drinfeld. Specifically, he proved that the strict lower bound \gamma is given by \frac \psi(0), where the function \psi is the convex hull of f(x)=e^ and g(x) = \frac. (Tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly influe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired. The harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations. As a simple example, the harmonic mean of 1, 4, and 4 is : \left(\frac\right)^ = \frac = \frac = 2\,. Definition The harmonic mean ''H'' of the positive real numbers x_1, x_2, \ldots, x_n is defined to be :H = \frac = \frac = \left(\frac\right)^. The third formula in the above equation expresses the harmonic mean as the reciprocal of the arithmetic mean of the reciprocals. From the following formula: :H = \frac. it is more apparent that the harmonic mean is related to the arithmetic and geometric means. It is the reciprocal dual of the arithmetic mean for positive inputs: :1/H(1/x_1 \ldots 1/x_n) = A(x_1 \ldots x_n) The harmonic mean is a Schur-con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clearing Denominators
In mathematics, the method of clearing denominators, also called clearing fractions, is a technique for simplifying an equation equating two expressions that each are a sum of rational expressions – which includes simple fractions. Example Consider the equation : \frac x 6 + \frac y = 1. The smallest common multiple of the two denominators 6 and 15''z'' is 30''z'', so one multiplies both sides by 30''z'': : 5xz + 2y = 30z. \, The result is an equation with no fractions. The simplified equation is not entirely equivalent to the original. For when we substitute and in the last equation, both sides simplify to 0, so we get , a mathematical truth. But the same substitution applied to the original equation results in , which is mathematically meaningless. Description Without loss of generality, we may assume that the right-hand side of the equation is 0, since an equation may equivalently be rewritten in the form . So let the equation have the form :\sum_^n \frac = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rearrangement Inequality
In mathematics, the rearrangement inequality states that x_n y_1 + \cdots + x_1 y_n \leq x_ y_1 + \cdots + x_ y_n \leq x_1 y_1 + \cdots + x_n y_n for every choice of real numbers x_1 \leq \cdots \leq x_n \quad \text \quad y_1 \leq \cdots \leq y_n and every permutation x_, \ldots, x_ of x_1, \ldots, x_n. If the numbers are different, meaning that x_1 < \cdots < x_n \quad \text \quad y_1 < \cdots < y_n, then the lower bound is attained only for the permutation which reverses the order, that is, for all and the upper bound is attained only for the identity, that is, for all Note that the rearrangement inequality makes no assumptions on the signs of the real numbers. Applications Many important inequalities can be proved by the rearrangement inequality, such as the[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert's Seventeenth Problem
Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It concerns the expression of positive definite rational functions as sums of quotients of squares. The original question may be reformulated as: * Given a multivariate polynomial that takes only non-negative values over the reals, can it be represented as a sum of squares of rational functions? Hilbert's question can be restricted to homogeneous polynomials of even degree, since a polynomial of odd degree changes sign, and the homogenization of a polynomial takes only nonnegative values if and only if the same is true for the polynomial. Motivation The formulation of the question takes into account that there are non-negative polynomials, for example :f(x,y,z)=z^6+x^4y^2+x^2y^4-3x^2y^2z^2, which cannot be represented as a sum of squares of other polynomials. In 1888, Hilbert showed that every non-negative homogeneous polynomial in ''n'' varia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-negative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
AM-HM
In mathematics, the three classical Pythagorean means are the arithmetic mean (AM), the geometric mean (GM), and the harmonic mean (HM). These means were studied with proportions by Pythagoreans and later generations of Greek mathematicians because of their importance in geometry and music. Definition They are defined by: :\begin \operatorname \left( x_1,\; \ldots,\; x_n \right) &= \frac \\ pt \operatorname \left( x_1,\; \ldots,\; x_n \right) &= \sqrt \\ pt \operatorname \left( x_1,\; \ldots,\; x_n \right) &= \frac \end Properties Each mean, \operatorname, has the following properties: ; First order homogeneity: \operatorname(bx_1,\, \ldots,\, bx_n) = b \operatorname(x_1,\, \ldots,\, x_n) ; Invariance under exchange: \operatorname(\ldots,\, x_i,\, \ldots,\, x_j,\, \ldots) = \operatorname(\ldots,\, x_j,\, \ldots,\, x_i,\, \ldots) : for any i and j. ; Monotonicity: a < b \rightarrow \operatorname(a,x_1,x_2,\ldots x_n) < \operatorname(b,x_1,x_2,\ldots x_n) ; |
Arithmetic Mean-geometric Mean Inequality
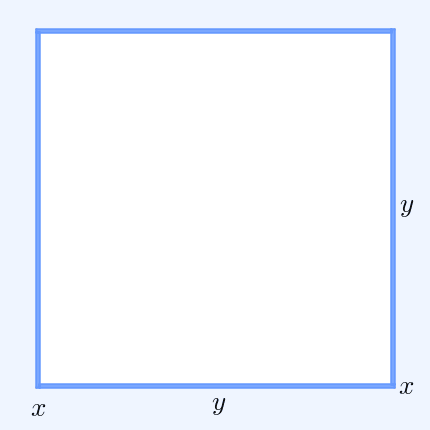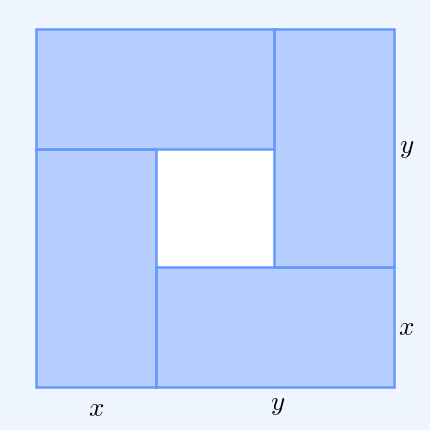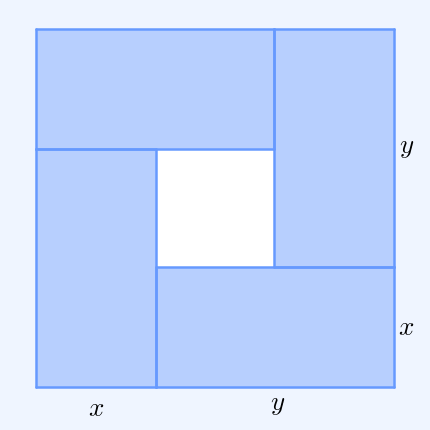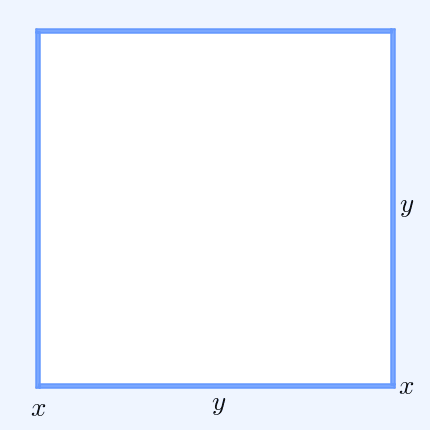
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number). The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbers and , is the statement that :\frac2 \ge \sqrt with equality if and only if . This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case of the binomial formula: :\begin 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end Hence , with equality precisely when , i.e. . The AM–GM inequality then follows from taking the positive square root of both sides and then dividing both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sedrakyan's Inequality
The following inequality is known as Sedrakyan's inequality, Bergström's inequality, Engel's form or Titu's lemma, respectively, referring to the article ''About the applications of one useful inequality'' of Nairi Sedrakyan published in 1997, to the book ''Problem-solving strategies'' of Arthur Engel published in 1998 and to the book ''Mathematical Olympiad Treasures'' of Titu Andreescu published in 2003. It is a direct consequence of Cauchy–Bunyakovsky–Schwarz inequality. Nevertheless, in his article (1997) Sedrakyan has noticed that written in this form this inequality can be used as a mathematical proof technique and it has very useful new applications. In the book ''Algebraic Inequalities'' (Sedrakyan) are provided several generalizations of this inequality. Statement of the inequality For any reals a_1, a_2, a_3, \ldots, a_n and positive reals b_1, b_2, b_3,\ldots, b_n, we have \frac + \frac + \cdots + \frac \geq \frac. (Nairi Sedrakyan (1997), Arthur Engel (199 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |