|
Normalization (statistics)
In statistics and applications of statistics, normalization can have a range of meanings. In the simplest cases, normalization of ratings means adjusting values measured on different scales to a notionally common scale, often prior to averaging. In more complicated cases, normalization may refer to more sophisticated adjustments where the intention is to bring the entire probability distributions of adjusted values into alignment. In the case of normalization of scores in educational assessment, there may be an intention to align distributions to a normal distribution. A different approach to normalization of probability distributions is quantile normalization, where the quantiles of the different measures are brought into alignment. In another usage in statistics, normalization refers to the creation of shifted and scaled versions of statistics, where the intention is that these normalized values allow the comparison of corresponding normalized values for different datasets in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Mean
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypothetical and potentially infinite group of objects conceived as a generalization from experience (e.g. the set of all possible hands in a game of poker). A population with finitely many values N in the support of the population distribution is a finite population with population size N. A population with infinitely many values in the support is called infinite population. A common aim of statistical analysis is to produce information about some chosen population. In statistical inference, a subset of the population (a statistical '' sample'') is chosen to represent the population in a statistical analysis. Moreover, the statistical sample must be unbiased and accurately model the population. The ratio of the size of this statistical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system theory, system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
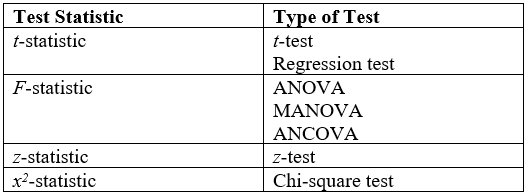
Test Statistic
Test statistic is a quantity derived from the sample for statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis. An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities of a descriptive stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
T-statistic
In statistics, the ''t''-statistic is the ratio of the difference in a number’s estimated value from its assumed value to its standard error. It is used in hypothesis testing via Student's ''t''-test. The ''t''-statistic is used in a ''t''-test to determine whether to support or reject the null hypothesis. It is very similar to the z-score but with the difference that ''t''-statistic is used when the sample size is small or the population standard deviation is unknown. For example, the ''t''-statistic is used in estimating the population mean from a sampling distribution of sample means if the population standard deviation is unknown. It is also used along with p-value when running hypothesis tests where the p-value tells us what the odds are of the results to have happened. Definition and features Let \hat\beta be an estimator of parameter ''β'' in some statistical model. Then a ''t''-statistic for this parameter is any quantity of the form : t_ = \frac, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T-distribution
In probability theory and statistics, Student's distribution (or simply the distribution) t_\nu is a continuous probability distribution that generalizes the Normal distribution#Standard normal distribution, standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped. However, t_\nu has Heavy-tailed distribution, heavier tails, and the amount of probability mass in the tails is controlled by the parameter \nu. For \nu = 1 the Student's distribution t_\nu becomes the standard Cauchy distribution, which has very fat-tailed distribution, "fat" tails; whereas for \nu \to \infty it becomes the standard normal distribution \mathcal(0, 1), which has very "thin" tails. The name "Student" is a pseudonym used by William Sealy Gosset in his scientific paper publications during his work at the Guinness Brewery in Dublin, Ireland. The Student's distribution plays a role in a number of widely used statistical analyses, including Student's t- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quality Control
Quality control (QC) is a process by which entities review the quality of all factors involved in production. ISO 9000 defines quality control as "a part of quality management focused on fulfilling quality requirements". This approach places emphasis on three aspects (enshrined in standards such as ISO 9001): # Elements such as controls, job management, defined and well managed processes, performance and integrity criteria, and identification of records # Competence, such as knowledge, skills, experience, and qualifications # Soft elements, such as personnel, integrity, confidence, organizational culture, motivation, team spirit, and quality relationships. Inspection is a major component of quality control, where physical product is examined visually (or the end results of a service are analyzed). Product inspectors will be provided with lists and descriptions of unacceptable product defects such as cracks or surface blemishes for example. History and introductio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ireland
Ireland (, ; ; Ulster Scots dialect, Ulster-Scots: ) is an island in the North Atlantic Ocean, in Northwestern Europe. Geopolitically, the island is divided between the Republic of Ireland (officially Names of the Irish state, named Irelanda sovereign state covering five-sixths of the island) and Northern Ireland (part of the United Kingdomcovering the remaining sixth). It is separated from Great Britain to its east by the North Channel (Great Britain and Ireland), North Channel, the Irish Sea, and St George's Channel. Ireland is the List of islands of the British Isles, second-largest island of the British Isles, the List of European islands by area, third-largest in Europe, and the List of islands by area, twentieth-largest in the world. As of 2022, the Irish population analysis, population of the entire island is just over 7 million, with 5.1 million in the Republic of Ireland and 1.9 million in Northern Ireland, ranking it the List of European islands by population, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guinness Brewery
St. James's Gate Brewery is a brewery founded in 1759 in Dublin, Ireland, by Arthur Guinness. The company is now a part of Diageo, a company formed from the merger of Guinness and Grand Metropolitan in 1997. The main product of the brewery is Draught Guinness. Originally leased in 1759 to Arthur Guinness at £45 per year for 9,000 years, the St. James's Gate area has been the home of Guinness ever since. It became the largest brewery in Ireland in 1838, and the largest in the world by 1886, with an annual output of 1.2 million barrels. Although no longer the largest brewery in the world, it remains as the largest brewer of stout. The company has since bought out the originally leased property, and during the 19th and early 20th centuries, the brewery owned most of the buildings in the surrounding area, including many streets of housing for brewery employees, and offices associated with the brewery. The brewery had its own power plant. There is an attached exhibition o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Sealy Gosset
William Sealy Gosset (13 June 1876 – 16 October 1937) was an English statistician, chemist and brewer who worked for Guinness. In statistics, he pioneered small sample experimental design. Gosset published under the pen name Student and developed Student's t-distribution – originally called Student's "z" – and "Student's test of statistical significance". Life and career Born in Canterbury, England, Canterbury, England the eldest son of Agnes Sealy Vidal and Colonel Frederic Gosset, R.E. Royal Engineers, Gosset attended Winchester College before matriculating as Winchester Scholar in natural sciences and mathematics at New College, Oxford. Upon graduating in 1899, he joined the brewery of Arthur Guinness & Son in Dublin, Ireland; he spent the rest of his 38-year career at Guinness. The site cites ''Dictionary of Scientific Biography'' (New York: Scribner's, 1972), pp. 476–477; ''International Encyclopedia of Statistics'', vol. I (New York: Free Press, 1978), pp. 409–4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ''p''-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe test of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Inference
Statistical inference is the process of using data analysis to infer properties of an underlying probability distribution.Upton, G., Cook, I. (2008) ''Oxford Dictionary of Statistics'', OUP. . Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population. In machine learning, the term ''inference'' is sometimes used instead to mean "make a prediction, by evaluating an already trained model"; in this context inferring properties of the model is referred to as ''training'' or ''learning'' (rather than ''inference''), and using a model for prediction is referred to as ''inference'' (instead of ''prediction''); se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |