Test Statistic

Test statistic is a quantity derived from the sample for statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis.

An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities of a descriptive statistic, and many statistics can be used as both test statistics and descriptive statistics. However, a test statistic is specifically intended for use in statistical testing, whereas the main quality of a descriptive statistic is that it is easily interpretable. Some informative descriptive statistics, such as the sample range, do not make good test statistics since it is difficult to determine their sampling distribution.

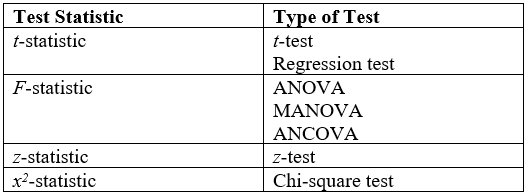
Two widely used test statistics are the t-statistic and the F-statistic.

Example

Suppose the task is to test whether a coin is fair (i.e. has equal probabilities of producing a head or a tail). If the coin is flipped 100 times and the results are recorded, the raw data can be represented as a sequence of 100 heads and tails. If there is interest in the marginal probability of obtaining a tail, only the number ''T'' out of the 100 flips that produced a tail needs to be recorded. But ''T'' can also be used as a test statistic in one of two ways:
*the exact sampling distribution of ''T'' under the null hypothesis is the binomial distribution with parameters 0.5 and 100.
*the value of ''T'' can be compared with its expected value under the null hypothesis of 50, and since the sample size is large, a normal distribution can be used as an approximation to the sampling distribution either for ''T'' or for the revised test statistic ''T''−50.

Using one of these sampling distributions, it is possible to compute either a one-tailed or two-tailed p-value for the null hypothesis that the coin is fair. The test statistic in this case reduces a set of 100 numbers to a single numerical summary that can be used for testing.

Common test statistics

One-sample tests are appropriate when a sample is being compared to the population from a hypothesis. The population characteristics are known from theory or are calculated from the population.

Two-sample tests are appropriate for comparing two samples, typically experimental and control samples from a scientifically controlled experiment.

Paired tests are appropriate for comparing two samples where it is impossible to control important variables. Rather than comparing two sets, members are paired between samples so the difference between the members becomes the sample. Typically the mean of the differences is then compared to zero. The common example scenario for when a paired difference test is appropriate is when a single set of test subjects has something applied to them and the test is intended to check for an effect.

Z-tests are appropriate for comparing means under stringent conditions regarding normality and a known standard deviation.

A ''t''-test is appropriate for comparing means under relaxed conditions (less is assumed).

Tests of proportions are analogous to tests of means (the 50% proportion).

Chi-squared tests use the same calculations and the same probability distribution for different applications:
* Chi-squared tests for variance are used to determine whether a normal population has a specified variance. The null hypothesis is that it does.
* Chi-squared tests of independence are used for deciding whether two variables are associated or are independent. The variables are categorical rather than numeric. It can be used to decide whether left-handedness is correlated with height (or not). The null hypothesis is that the variables are independent. The numbers used in the calculation are the observed and expected frequencies of occurrence (from contingency tables).
* Chi-squared goodness of fit tests are used to determine the adequacy of curves fit to data. The null hypothesis is that the curve fit is adequate. It is common to determine curve shapes to minimize the mean square error, so it is appropriate that the goodness-of-fit calculation sums the squared errors.

F-tests (analysis of variance, ANOVA) are commonly used when deciding whether groupings of data by category are meaningful. If the variance of test scores of the left-handed in a class is much smaller than the variance of the whole class, then it may be useful to study lefties as a group. The null hypothesis is that two variances are the same – so the proposed grouping is not meaningful.

In the table below, the symbols used are defined at the bottom of the table. Many other tests can be found in other articles. Proofs exist that the test statistics are appropriate. Abstract: "The focus was on the Neyman–Pearson approach to hypothesis testing. A brief historical development of the Neyman–Pearson approach is followed by mathematical proofs of each of the hypothesis tests covered in the reference material." The proofs do not reference the concepts introduced by Neyman and Pearson, instead they show that traditional test statistics have the probability distributions ascribed to them, so that significance calculations assuming those distributions are correct. The thesis information is also posted at mathnstats.com as of April 2013.

See also

* Null distribution
* Likelihood-ratio test
* Neyman–Pearson lemma
* $R^2$ = coefficient of determination
* Sufficiency (statistics)

References

{{DEFAULTSORT:Test Statistic
Statistical hypothesis testing
Sample statistics