|
Nonlinear
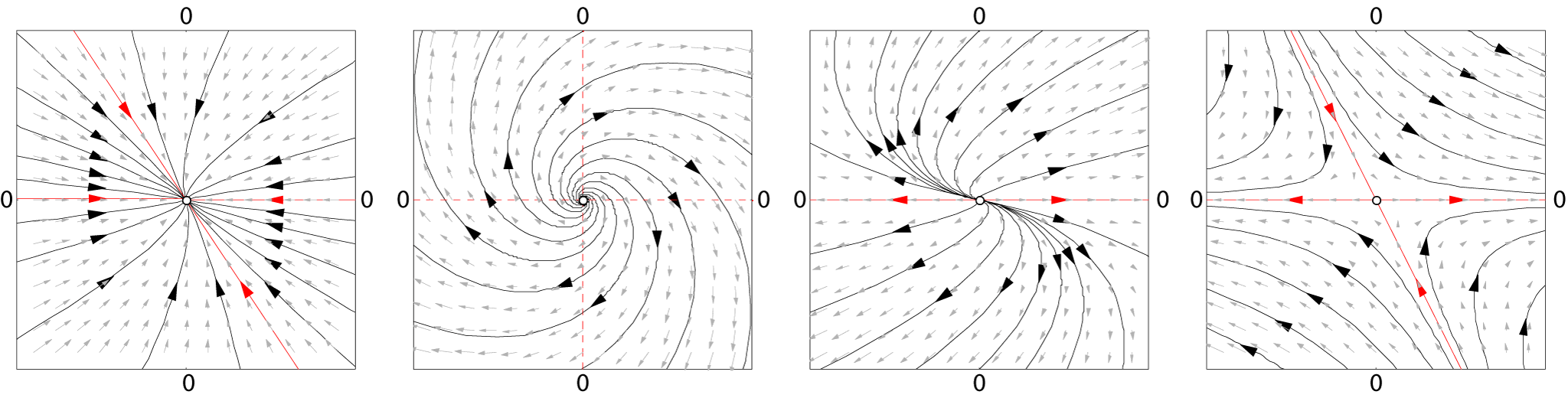
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soliton
In mathematics and physics, a soliton is a nonlinear, self-reinforcing, localized wave packet that is , in that it preserves its shape while propagating freely, at constant velocity, and recovers it even after collisions with other such localized wave packets. Its remarkable stability can be traced to a balanced cancellation of nonlinear and dispersive effects in the medium.Dispersive effects are a property of certain systems where the speed of a wave depends on its frequency. Solitons were subsequently found to provide stable solutions of a wide class of weakly nonlinear dispersive partial differential equations describing physical systems. The soliton phenomenon was first described in 1834 by John Scott Russell who observed a solitary wave in the Union Canal in Scotland. He reproduced the phenomenon in a wave tank and named it the " Wave of Translation". The Korteweg–de Vries equation was later formulated to model such waves, and the term "soliton" was coined by Zabu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
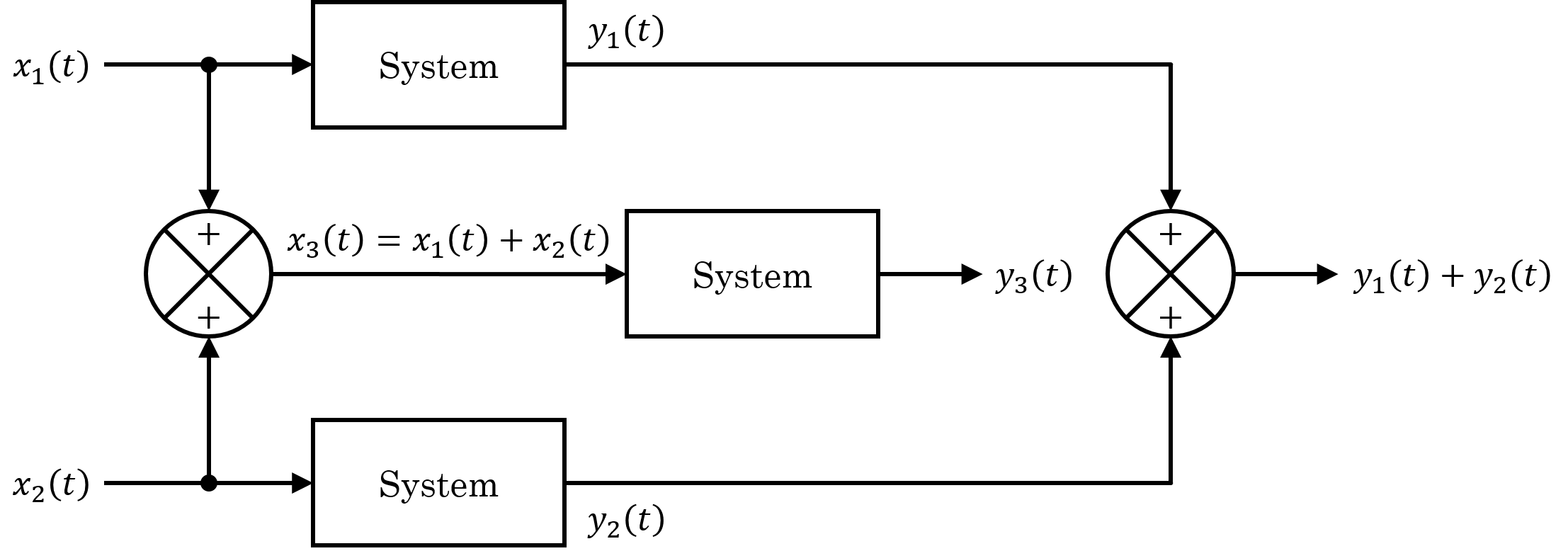
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'', and input ''B'' produces response ''Y'', then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1 + x_2) = F(x_1) + F(x_2) and homogeneity F(ax) = a F(x) for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stanisław Ulam
Stanisław Marcin Ulam ( ; 13 April 1909 – 13 May 1984) was a Polish and American mathematician, nuclear physicist and computer scientist. He participated in the Manhattan Project, originated the History of the Teller–Ulam design, Teller–Ulam design of thermonuclear weapons, discovered the concept of the cellular automaton, invented the Monte Carlo method, Monte Carlo method of computation, and suggested nuclear pulse propulsion. In pure and applied mathematics, he proved a number of theorems and proposed several conjectures. Born into a wealthy Polish Jewish family in Lemberg, Austria-Hungary; Ulam studied mathematics at the Lviv Polytechnic#Second Polish Republic, Lwów Polytechnic Institute, where he earned his PhD in 1933 under the supervision of Kazimierz Kuratowski and Włodzimierz Stożek. In 1935, John von Neumann, whom Ulam had met in Warsaw, invited him to come to the Institute for Advanced Study in Princeton, New Jersey, for a few months. From 1936 to 1939, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearization
In mathematics, linearization (British English: linearisation) is finding the linear approximation to a function at a given point. The linear approximation of a function is the first order Taylor expansion around the point of interest. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or discrete dynamical systems. This method is used in fields such as engineering, physics, economics, and ecology. Linearization of a function Linearizations of a function are lines—usually lines that can be used for purposes of calculation. Linearization is an effective method for approximating the output of a function y = f(x) at any x = a based on the value and slope of the function at x = b, given that f(x) is differentiable on , b/math> (or , a/math>) and that a is close to b. In short, linearization approximates the output of a function near x = a. For example, \sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in French an ''équation'' is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation. Solving an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables. The " =" symbol, which appears in every equati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example, The set of all rational numbers is often referred to as "the rationals", and is closed under addition, subtraction, multiplication, and division by a nonzero rational number. It is a field under these operations and therefore also called the field of rationals or the field of rational numbers. It is usually denoted by boldface , or blackboard bold A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |