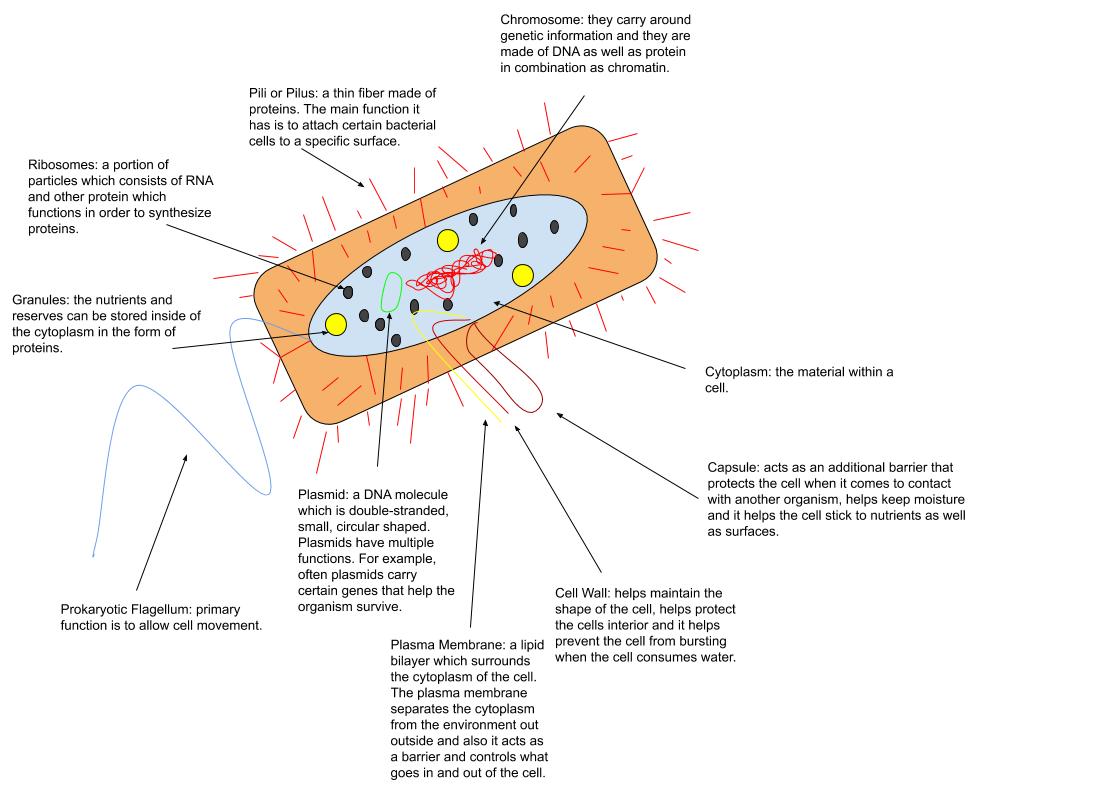
|
Moran Process
A Moran process or Moran model is a simple stochastic process used in biology to describe finite populations. The process is named after Patrick Moran, who first proposed the model in 1958. It can be used to model variety-increasing processes such as mutation as well as variety-reducing effects such as genetic drift and natural selection. The process can describe the probabilistic dynamics in a finite population of constant size ''N'' in which two alleles A and B are competing for dominance. The two alleles are considered to be true replicators (i.e. entities that make copies of themselves). In each time step a random individual (which is of either type A or B) is chosen for reproduction and a random individual is chosen for death; thus ensuring that the population size remains constant. To model selection, one type has to have a higher fitness and is thus more likely to be chosen for reproduction. The same individual can be chosen for death and for reproduction in the same step ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance. Applications and the study of phenomena have in turn inspired the proposal of new stochastic processes. Examples of such stochastic processes include the Wiener process or Brownian motion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Total Expectation
The proposition in probability theory known as the law of total expectation, the law of iterated expectations (LIE), Adam's law, the tower rule, and the smoothing theorem, among other names, states that if X is a random variable whose expected value \operatorname(X) is defined, and Y is any random variable on the same probability space, then :\operatorname (X) = \operatorname ( \operatorname ( X \mid Y)), i.e., the expected value of the conditional expected value of X given Y is the same as the expected value of X. One special case states that if _i is a finite or countable partition of the sample space, then :\operatorname (X) = \sum_i. Note: The conditional expected value E(''X'' , ''Z'') is a random variable whose value depend on the value of ''Z''. Note that the conditional expected value of ''X'' given the ''event'' ''Z'' = ''z'' is a function of ''z''. If we write E(''X'' , ''Z'' = ''z'') = ''g''(''z'') then the random variable E(''X'' , ''Z'') is ''g''(''Z'') ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolutionary Dynamics
Evolutionary dynamics is the study of the mathematical principles according to which biological organisms as well as cultural ideas evolve and evolved. This is mostly achieved through the mathematical discipline of population genetics, along with evolutionary game theory. Most population genetics considers changes in the frequencies of alleles at a small number of gene loci. When infinitesimal effects at a large number of gene loci are considered, one derives quantitative genetics. Traditional population genetic models deal with alleles and genotypes, and are frequently stochastic. In evolutionary game theory, developed first by John Maynard Smith, evolutionary biology concepts may take a deterministic mathematical form, with selection acting directly on inherited phenotypes. These same models can be applied to studying the evolution of human preferences and ideologies. Many variants on these models have been developed, which incorporate weak selection, mutual population structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Clock
The molecular clock is a figurative term for a technique that uses the mutation rate of biomolecules to deduce the time in prehistory when two or more life forms diverged. The biomolecular data used for such calculations are usually nucleotide sequences for DNA, RNA, or amino acid sequences for proteins. The benchmarks for determining the mutation rate are often fossil or archaeological dates. The molecular clock was first tested in 1962 on the hemoglobin protein variants of various animals, and is commonly used in molecular evolution to estimate times of speciation or radiation. It is sometimes called a gene clock or an evolutionary clock. Early discovery and genetic equidistance The notion of the existence of a so-called "molecular clock" was first attributed to Émile Zuckerkandl and Linus Pauling who, in 1962, noticed that the number of amino acid differences in hemoglobin between different lineages changes roughly linearly with time, as estimated from fossil ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector field flux behaves like a source at a given point. It is a local measure of its "outgoingness" – the extent t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Species
In biology, a species is the basic unit of Taxonomy (biology), classification and a taxonomic rank of an organism, as well as a unit of biodiversity. A species is often defined as the largest group of organisms in which any two individuals of the appropriate sexes or mating types can reproduction, produce Fertility, fertile offspring, typically by sexual reproduction. Other ways of defining species include their karyotype, DNA sequence, morphology (biology), morphology, behaviour or ecological niche. In addition, paleontologists use the concept of the chronospecies since fossil reproduction cannot be examined. The most recent rigorous estimate for the total number of species of eukaryotes is between 8 and 8.7 million. However, only about 14% of these had been described by 2011. All species (except viruses) are given a binomial nomenclature, two-part name, a "binomial". The first part of a binomial is the genus to which the species belongs. The second part is called the specifi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genome
In the fields of molecular biology and genetics, a genome is all the genetic information of an organism. It consists of nucleotide sequences of DNA (or RNA in RNA viruses). The nuclear genome includes protein-coding genes and non-coding genes, other functional regions of the genome such as regulatory sequences (see non-coding DNA), and often a substantial fraction of 'junk' DNA with no evident function. Almost all eukaryotes have mitochondria and a small mitochondrial genome. Algae and plants also contain chloroplasts with a chloroplast genome. The study of the genome is called genomics. The genomes of many organisms have been sequenced and various regions have been annotated. The International Human Genome Project reported the sequence of the genome for ''Homo sapiens'' in 200The Human Genome Project although the initial "finished" sequence was missing 8% of the genome consisting mostly of repetitive sequences. With advancements in technology that could handle seq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutral Theory Of Evolution
The neutral theory of molecular evolution holds that most evolutionary changes occur at the molecular level, and most of the variation within and between species are due to random genetic drift of mutant alleles that are selectively neutral. The theory applies only for evolution at the molecular level, and is compatible with phenotypic evolution being shaped by natural selection as postulated by Charles Darwin. The neutral theory allows for the possibility that most mutations are deleterious, but holds that because these are rapidly removed by natural selection, they do not make significant contributions to variation within and between species at the molecular level. A neutral mutation is one that does not affect an organism's ability to survive and reproduce. The neutral theory assumes that most mutations that are not deleterious are neutral rather than beneficial. Because only a fraction of gametes are sampled in each generation of a species, the neutral theory suggests that a mu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
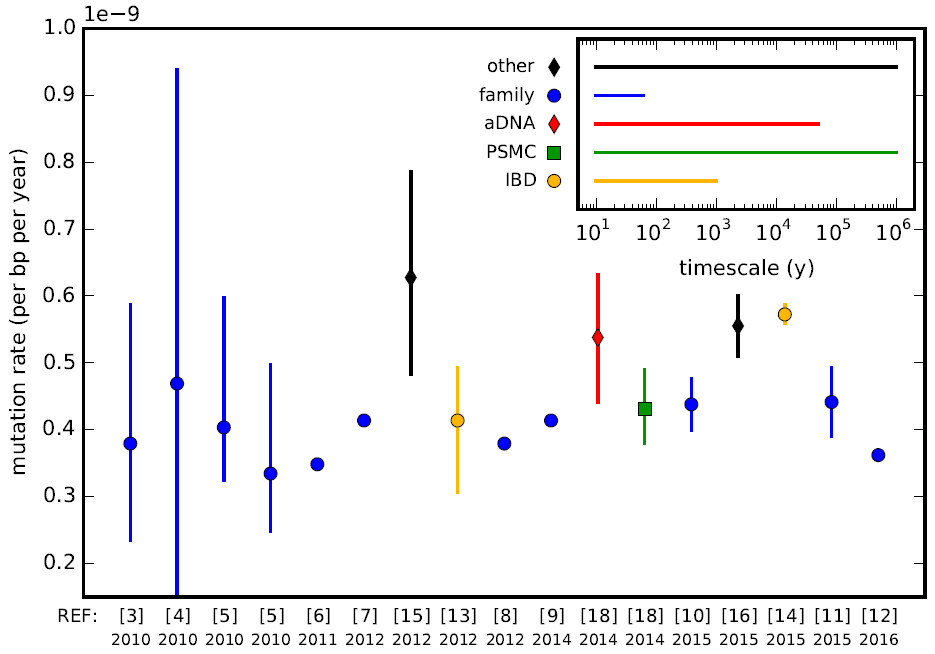
Mutation Rate
In genetics, the mutation rate is the frequency of new mutations in a single gene or organism over time. Mutation rates are not constant and are not limited to a single type of mutation; there are many different types of mutations. Mutation rates are given for specific classes of mutations. Point mutations are a class of mutations which are changes to a single base. Missense mutation, Missense and Nonsense mutations are two subtypes of point mutations. The rate of these types of substitutions can be further subdivided into a mutation spectrum which describes the influence of the genetic context on the mutation rate. There are several natural units of time for each of these rates, with rates being characterized either as mutations per base pair per cell division, per gene per generation, or per genome per generation. The mutation rate of an organism is an evolved characteristic and is strongly influenced by the genetics of each organism, in addition to strong influence from the envi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolutionary Game Theory
Evolutionary game theory (EGT) is the application of game theory to evolving populations in biology. It defines a framework of contests, strategies, and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith and George R. Price's formalisation of contests, analysed as strategies, and the mathematical criteria that can be used to predict the results of competing strategies. Evolutionary game theory differs from classical game theory in focusing more on the dynamics of strategy change. This is influenced by the frequency of the competing strategies in the population. Evolutionary game theory has helped to explain the basis of altruistic behaviours in Darwinian evolution. It has in turn become of interest to economists, sociologists, anthropologists, and philosophers. History Classical game theory Classical non-cooperative game theory was conceived by John von Neumann to determine optimal strategies in competitions between ad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrence Relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |