|
Monotonicity (mechanism Design)
In mechanism design, monotonicity is a property of a social choice function. It is a necessary condition for being able to implement the function using a strategyproof mechanism. Its verbal description is: In other words: Notation There is a set X of possible outcomes. There are n agents which have different valuations for each outcome. The valuation of agent i is represented as a function: v_i : X \longrightarrow R_+ which expresses the value it assigns to each alternative. The vector of all value-functions is denoted by v. For every agent i, the vector of all value-functions of the ''other'' agents is denoted by v_. So v \equiv (v_i,v_). A social choice function is a function that takes as input the value-vector v and returns an outcome x\in X. It is denoted by \text(v) or \text(v_i,v_). In mechanisms without money A social choice function satisfies the strong monotonicity property (SMON) if for every agent i and every v_i,v_i',v_, if: x = \text(v_i, v_) x' = \tex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanism Design
Mechanism design is a field in economics and game theory that takes an objectives-first approach to designing economic mechanisms or incentives, toward desired objectives, in strategic settings, where players act rationally. Because it starts at the end of the game, then goes backwards, it is also called reverse game theory. It has broad applications, from economics and politics in such fields as market design, auction theory and social choice theory to networked-systems (internet interdomain routing, sponsored search auctions). Mechanism design studies solution concepts for a class of private-information games. Leonid Hurwicz explains that 'in a design problem, the goal function is the main "given", while the mechanism is the unknown. Therefore, the design problem is the "inverse" of traditional economic theory, which is typically devoted to the analysis of the performance of a given mechanism.' So, two distinguishing features of these games are: * that a game "designer" ch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice
Social choice theory or social choice is a theoretical framework for analysis of combining individual opinions, preferences, interests, or welfares to reach a ''collective decision'' or ''social welfare'' in some sense.Amartya Sen (2008). "Social Choice,". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> Whereas choice theory is concerned with individuals making choices based on their preferences, social choice theory is concerned with how to translate the preferences of individuals into the preferences of a group. A non-theoretical example of a collective decision is enacting a law or set of laws under a constitution. Another example is voting, where individual preferences over candidates are collected to elect a person that best represents the group's preferences. Social choice blends elements of welfare economics and public choice theory. It is methodologically individualistic, in that it aggregates preferences and behaviors of individual memb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strategyproof
In game theory, an asymmetric game where players have private information is said to be strategy-proof or strategyproof (SP) if it is a weakly-dominant strategy for every player to reveal his/her private information, i.e. given no information about what the others do, you fare best or at least not worse by being truthful. SP is also called truthful or dominant-strategy-incentive-compatible (DSIC), to distinguish it from other kinds of incentive compatibility. An SP game is not always immune to collusion, but its robust variants are; with group strategyproofness no group of people can collude to misreport their preferences in a way that makes every member better off, and with strong group strategyproofness no group of people can collude to misreport their preferences in a way that makes at least one member of the group better off without making any of the remaining members worse off. Examples Typical examples of SP mechanisms are majority voting between two alternatives, second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-parameter Utility
In mechanism design, an agent is said to have single-parameter utility if his valuation of the possible outcomes can be represented by a single number. For example, in an auction for a single item, the utilities of all agents are single-parametric, since they can be represented by their monetary evaluation of the item. In contrast, in a combinatorial auction for two or more related items, the utilities are usually not single-parametric, since they are usually represented by their evaluations to all possible bundles of items. Notation There is a set X of possible outcomes. There are n agents which have different valuations for each outcome. In general, each agent can assign a different and unrelated value to every outcome in X. In the special case of single-parameter utility, each agent i has a publicly known outcome proper subset W_i \subset X which are the "winning outcomes" for agent i (e.g., in a single-item auction, W_i contains the outcome in which agent i wins the item). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
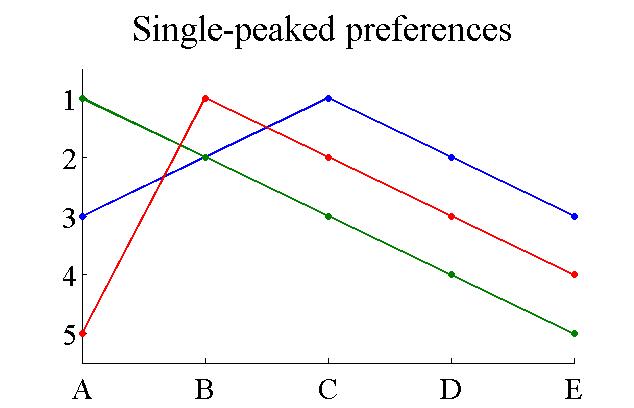
Single Peaked Preferences
Single-peaked preferences are a class of preference relations. A group of agents is said to have single-peaked preferences over a set of possible outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and - # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome: it is to select the median quantity. See the median voter theorem. It is truthful because the median function satisfies the strong monotonicity proper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truthful Mechanism
In game theory, an asymmetric game where players have private information is said to be strategy-proof or strategyproof (SP) if it is a weakly-dominant strategy for every player to reveal his/her private information, i.e. given no information about what the others do, you fare best or at least not worse by being truthful. SP is also called truthful or dominant-strategy-incentive-compatible (DSIC), to distinguish it from other kinds of incentive compatibility. An SP game is not always immune to collusion, but its robust variants are; with group strategyproofness no group of people can collude to misreport their preferences in a way that makes every member better off, and with strong group strategyproofness no group of people can collude to misreport their preferences in a way that makes at least one member of the group better off without making any of the remaining members worse off. Examples Typical examples of SP mechanisms are majority voting between two alternatives, secon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
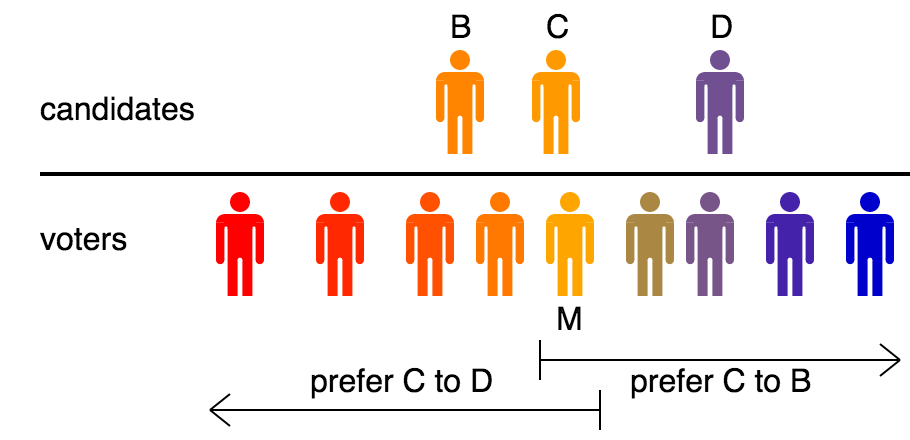
Median Voter Theorem
The median voter theorem is a proposition relating to ranked preference voting put forward by Duncan Black in 1948.Duncan Black, "On the Rationale of Group Decision-making" (1948). It states that if voters and policies are distributed along a one-dimensional spectrum, with voters ranking alternatives in order of proximity, then any voting method which satisfies the Condorcet criterion will elect the candidate closest to the median voter. In particular, a majority vote between two options will do so. The theorem is associated with public choice economics and statistical political science. Partha Dasgupta and Eric Maskin have argued that it provides a powerful justification for voting methods based on the Condorcet criterion. Plott's majority rule equilibrium theorem extends this to two dimensions. A loosely related assertion had been made earlier (in 1929) by Harold Hotelling. It is not a true theorem and is more properly known as the median voter theory or median voter model. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinal Utility
In economics, a cardinal utility function or scale is a utility index that preserves preference orderings uniquely up to positive affine transformations. Two utility indices are related by an affine transformation if for the value u(x_i) of one index ''u'', occurring at any quantity x_i of the goods bundle being evaluated, the corresponding value v(x_i) of the other index ''v'' satisfies a relationship of the form :v(x_i) = au(x_i) + b\!, for fixed constants ''a'' and ''b''. Thus the utility functions themselves are related by :v(x) = au(x) + b. The two indices differ only with respect to scale and origin. Thus if one is concave, so is the other, in which case there is often said to be diminishing marginal utility. Thus the use of cardinal utility imposes the assumption that levels of absolute satisfaction exist, so that the magnitudes of increments to satisfaction can be compared across different situations. In consumer choice theory, ordinal utility with its weaker assumpti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utilitarian
In ethical philosophy, utilitarianism is a family of normative ethical theories that prescribe actions that maximize happiness and well-being for all affected individuals. Although different varieties of utilitarianism admit different characterizations, the basic idea behind all of them is, in some sense, to maximize utility, which is often defined in terms of well-being or related concepts. For instance, Jeremy Bentham, the founder of utilitarianism, described ''utility'' as: That property in any object, whereby it tends to produce benefit, advantage, pleasure, good, or happiness ... rto prevent the happening of mischief, pain, evil, or unhappiness to the party whose interest is considered. Utilitarianism is a version of consequentialism, which states that the consequences of any action are the only standard of right and wrong. Unlike other forms of consequentialism, such as egoism and altruism, utilitarianism considers the interests of all sentient beings equally. Pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-parameter Utility
In mechanism design, an agent is said to have single-parameter utility if his valuation of the possible outcomes can be represented by a single number. For example, in an auction for a single item, the utilities of all agents are single-parametric, since they can be represented by their monetary evaluation of the item. In contrast, in a combinatorial auction for two or more related items, the utilities are usually not single-parametric, since they are usually represented by their evaluations to all possible bundles of items. Notation There is a set X of possible outcomes. There are n agents which have different valuations for each outcome. In general, each agent can assign a different and unrelated value to every outcome in X. In the special case of single-parameter utility, each agent i has a publicly known outcome proper subset W_i \subset X which are the "winning outcomes" for agent i (e.g., in a single-item auction, W_i contains the outcome in which agent i wins the item). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Makespan
In operations research, the makespan of a project is the length of time that elapses from the start of work to the end. This type of multi-mode resource constrained project scheduling problem (MRCPSP) seeks to create the shortest logical project schedule, by efficiently using project resources, adding the lowest number of additional resources as possible to achieve the minimum makespan. ', Afshar-Nadjafi, B, ''in Applied Computing and Informatics (2014) The term commonly appears in the context of |