median voter theorem on:
[Wikipedia]
[Google]
[Amazon]
The median voter theorem is a proposition relating to ranked preference voting put forward by
Duncan Black
Duncan Black, FBA (23 May 1908 – 14 January 1991) was a Scottish economist who laid the foundations of social choice theory. In particular he was responsible for unearthing the work of many early political scientists, including Charles Lutw ...
in 1948.Duncan Black, "On the Rationale of Group Decision-making" (1948). It states that if voters and policies are distributed along a one-dimensional spectrum
A spectrum (plural ''spectra'' or ''spectrums'') is a condition that is not limited to a specific set of values but can vary, without gaps, across a continuum. The word was first used scientifically in optics to describe the rainbow of colors i ...
, with voters ranking alternatives in order of proximity, then any voting method which satisfies the Condorcet criterion
An electoral system satisfies the Condorcet winner criterion () if it always chooses the Condorcet winner when one exists. The candidate who wins a majority of the vote in every head-to-head election against each of the other candidatesthat is, a ...
will elect the candidate closest to the median voter. In particular, a majority vote
A majority, also called a simple majority or absolute majority to distinguish it from related terms, is more than half of the total.Dictionary definitions of ''majority'' aMerriam-Websterpublic choice economics and statistical
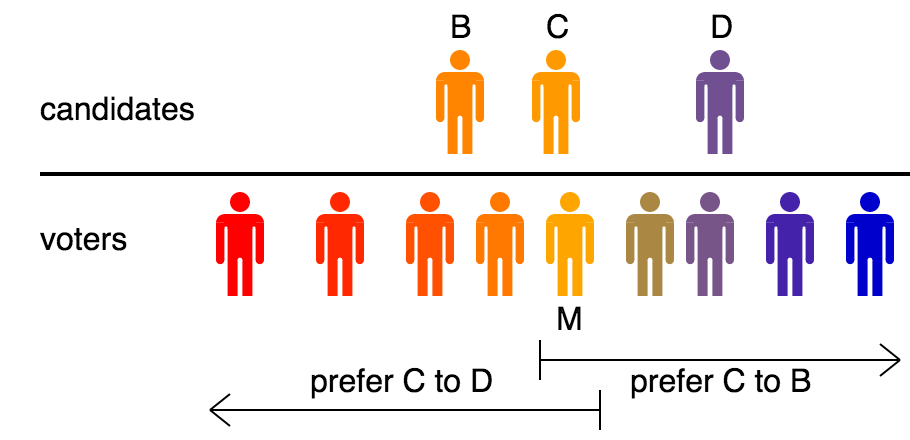 Assume that there is an odd number of voters and at least two candidates, and assume that opinions are distributed along a spectrum. Assume that each voter ranks the candidates in an order of proximity such that the candidate closest to the voter receives their first preference, the next closest receives their second preference, and so forth. Then there is a median voter and we will show that the election will be won by the candidate who is closest to him or her.
Proof — Let the median voter be Marlene. The candidate who is closest to her will receive her first preference vote. Suppose that this candidate is Charles and that he lies to her left. Then Marlene and all voters to her left (comprising a majority of the electorate) will prefer Charles to all candidates to his right, and Marlene and all voters to her right will prefer Charles to all candidates to his left. ∎
The Condorcet criterion is defined as being satisfied by any voting method which ensures that a candidate who is preferred to every other candidate by a majority of the electorate will be the winner, and this is precisely the case with Charles here; so it follows that Charles will win any election conducted using a method satisfying the Condorcet criterion.
Hence under any voting method which satisfies the Condorcet criterion the winner will be the candidate preferred by the median voter. For binary decisions the majority vote satisfies the criterion; for multiway votes several methods satisfy it (see
Assume that there is an odd number of voters and at least two candidates, and assume that opinions are distributed along a spectrum. Assume that each voter ranks the candidates in an order of proximity such that the candidate closest to the voter receives their first preference, the next closest receives their second preference, and so forth. Then there is a median voter and we will show that the election will be won by the candidate who is closest to him or her.
Proof — Let the median voter be Marlene. The candidate who is closest to her will receive her first preference vote. Suppose that this candidate is Charles and that he lies to her left. Then Marlene and all voters to her left (comprising a majority of the electorate) will prefer Charles to all candidates to his right, and Marlene and all voters to her right will prefer Charles to all candidates to his left. ∎
The Condorcet criterion is defined as being satisfied by any voting method which ensures that a candidate who is preferred to every other candidate by a majority of the electorate will be the winner, and this is precisely the case with Charles here; so it follows that Charles will win any election conducted using a method satisfying the Condorcet criterion.
Hence under any voting method which satisfies the Condorcet criterion the winner will be the candidate preferred by the median voter. For binary decisions the majority vote satisfies the criterion; for multiway votes several methods satisfy it (see
 The median voter theorem applies in a restricted form to distributions of voter opinions in spaces of any dimension. A distribution in more than one dimension does not necessarily have a median in all directions (which might be termed an 'omnidirectional median'); however a broad class of rotationally symmetric distributions, including the
The median voter theorem applies in a restricted form to distributions of voter opinions in spaces of any dimension. A distribution in more than one dimension does not necessarily have a median in all directions (which might be termed an 'omnidirectional median'); however a broad class of rotationally symmetric distributions, including the
"Multidimensional Voting Models"
(2016). (Uniqueness here generalises the property guaranteed by oddness of sample size in a single dimension.) ''Proof''. See the diagram, in which the grey disc represents the voter distribution as uniform over a circle and M is the median in all directions. Let A and B be two candidates, of whom A is the closer to the median. Then the voters who rank A above B are precisely the ones to the left (i.e. the 'A' side) of the solid red line; and since A is closer than B to M, the median is also to the left of this line. Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B. ∎
It follows that all Condorcet methods – and also Coombs' – satisfy the median voter property in spaces of any dimension for voter distributions with omnidirectional medians.
It is easy to construct voter distributions which do not have a median in all directions. The simplest example consists of a distribution limited to 3 points not lying in a straight line, such as 1, 2 and 3 in the second diagram. Each voter location coincides with the median under a certain set of one-dimensional projections. If A, B and C are the candidates, then '1' will vote A-B-C, '2' will vote B-C-A, and '3' will vote C-A-B, giving a Condorcet cycle. This is the subject of the McKelvey–Schofield theorem.
Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B. ∎
It follows that all Condorcet methods – and also Coombs' – satisfy the median voter property in spaces of any dimension for voter distributions with omnidirectional medians.
It is easy to construct voter distributions which do not have a median in all directions. The simplest example consists of a distribution limited to 3 points not lying in a straight line, such as 1, 2 and 3 in the second diagram. Each voter location coincides with the median under a certain set of one-dimensional projections. If A, B and C are the candidates, then '1' will vote A-B-C, '2' will vote B-C-A, and '3' will vote C-A-B, giving a Condorcet cycle. This is the subject of the McKelvey–Schofield theorem.
 ''Lemma''. Whenever a discrete distribution has a median ''M'' in all directions, the data points not located at ''M'' must come in balanced pairs (''A'',A ' ) on either side of ''M'' with the property that ''A'' – ''M'' – A ' is a straight line (ie. ''not'' like ''A'' 0 – ''M'' – ''A'' 2 in the diagram).
''Proof''. This result was proved algebraically by Charles Plott in 1967. Here we give a simple geometric proof by contradiction in two dimensions.
Suppose, on the contrary, that there is a set of points ''Ai'' which have ''M'' as median in all directions, but for which the points not coincident with ''M'' do not come in balanced pairs. Then we may remove from this set any points at ''M'', and any balanced pairs about ''M'', without ''M'' ceasing to be a median in any direction; so ''M'' remains an omnidirectional median.
If the number of remaining points is odd, then we can easily draw a line through ''M'' such that the majority of points lie on one side of it, contradicting the median property of ''M''.
If the number is even, say 2''n'', then we can label the points ''A'' 0, ''A''1,... in clockwise order about ''M'' starting at any point (see the diagram). Let θ be the angle subtended by the arc from ''M'' –''A'' 0 to ''M'' –''A'' ''n'' . Then if θ < 180° as shown, we can draw a line similar to the broken red line through ''M'' which has the majority of data points on one side of it, again contradicting the median property of ''M'' ; whereas if θ > 180° the same applies with the majority of points on the other side. And if θ = 180°, then ''A'' 0 and ''A'' ''n'' form a balanced pair, contradicting another assumption. ∎
''Theorem''. Whenever a discrete distribution has a median ''M'' in all directions, it coincides with its geometric median.
''Proof''. The sum of distances from any point ''P'' to a set of data points in balanced pairs (''A'',A ' ) is the sum of the lengths ''A'' – ''P'' – A '. Each individual length of this form is minimised over ''P'' when the line is straight, as happens when ''P'' coincides with ''M''. The sum of distances from ''P'' to any data points located at ''M'' is likewise minimised when ''P'' and ''M'' coincide. Thus the sum of distances from the data points to ''P'' is minimised when ''P'' coincides with ''M'' . ∎
''Lemma''. Whenever a discrete distribution has a median ''M'' in all directions, the data points not located at ''M'' must come in balanced pairs (''A'',A ' ) on either side of ''M'' with the property that ''A'' – ''M'' – A ' is a straight line (ie. ''not'' like ''A'' 0 – ''M'' – ''A'' 2 in the diagram).
''Proof''. This result was proved algebraically by Charles Plott in 1967. Here we give a simple geometric proof by contradiction in two dimensions.
Suppose, on the contrary, that there is a set of points ''Ai'' which have ''M'' as median in all directions, but for which the points not coincident with ''M'' do not come in balanced pairs. Then we may remove from this set any points at ''M'', and any balanced pairs about ''M'', without ''M'' ceasing to be a median in any direction; so ''M'' remains an omnidirectional median.
If the number of remaining points is odd, then we can easily draw a line through ''M'' such that the majority of points lie on one side of it, contradicting the median property of ''M''.
If the number is even, say 2''n'', then we can label the points ''A'' 0, ''A''1,... in clockwise order about ''M'' starting at any point (see the diagram). Let θ be the angle subtended by the arc from ''M'' –''A'' 0 to ''M'' –''A'' ''n'' . Then if θ < 180° as shown, we can draw a line similar to the broken red line through ''M'' which has the majority of data points on one side of it, again contradicting the median property of ''M'' ; whereas if θ > 180° the same applies with the majority of points on the other side. And if θ = 180°, then ''A'' 0 and ''A'' ''n'' form a balanced pair, contradicting another assumption. ∎
''Theorem''. Whenever a discrete distribution has a median ''M'' in all directions, it coincides with its geometric median.
''Proof''. The sum of distances from any point ''P'' to a set of data points in balanced pairs (''A'',A ' ) is the sum of the lengths ''A'' – ''P'' – A '. Each individual length of this form is minimised over ''P'' when the line is straight, as happens when ''P'' coincides with ''M''. The sum of distances from ''P'' to any data points located at ''M'' is likewise minimised when ''P'' and ''M'' coincide. Thus the sum of distances from the data points to ''P'' is minimised when ''P'' coincides with ''M'' . ∎
The Median Voter Model
Political science theories Public choice theory Voting theory Game theory Mathematical economics
political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and power, and the analysis of political activities, political thought, political behavior, and associated constitutions and la ...
. Partha Dasgupta
Sir Partha Sarathi Dasgupta (born on 17 November 1942), is an Indian-British economist who is the Frank Ramsey Professor Emeritus of Economics at the University of Cambridge, United Kingdom and Fellow of St John's College, Cambridge.
Personal ...
and Eric Maskin
Eric Stark Maskin (born December 12, 1950) is an American economist and mathematician. He was jointly awarded the 2007 Nobel Memorial Prize in Economic Sciences with Leonid Hurwicz and Roger Myerson "for having laid the foundations of mechanism d ...
have argued that it provides a powerful justification for voting methods based on the Condorcet criterion. Plott's majority rule equilibrium theorem extends this to two dimensions.
A loosely related assertion had been made earlier (in 1929) by Harold Hotelling
Harold Hotelling (; September 29, 1895 – December 26, 1973) was an American mathematical statistician and an influential economic theorist, known for Hotelling's law, Hotelling's lemma, and Hotelling's rule in economics, as well as Hotelling's T ...
. It is not a true theorem and is more properly known as the median voter theory or median voter model. It says that in a representative democracy
Representative democracy, also known as indirect democracy, is a type of democracy where elected people represent a group of people, in contrast to direct democracy. Nearly all modern Western-style democracies function as some type of represen ...
, politicians will converge to the viewpoint of the median voter.
Statement and proof of the theorem
 Assume that there is an odd number of voters and at least two candidates, and assume that opinions are distributed along a spectrum. Assume that each voter ranks the candidates in an order of proximity such that the candidate closest to the voter receives their first preference, the next closest receives their second preference, and so forth. Then there is a median voter and we will show that the election will be won by the candidate who is closest to him or her.
Proof — Let the median voter be Marlene. The candidate who is closest to her will receive her first preference vote. Suppose that this candidate is Charles and that he lies to her left. Then Marlene and all voters to her left (comprising a majority of the electorate) will prefer Charles to all candidates to his right, and Marlene and all voters to her right will prefer Charles to all candidates to his left. ∎
The Condorcet criterion is defined as being satisfied by any voting method which ensures that a candidate who is preferred to every other candidate by a majority of the electorate will be the winner, and this is precisely the case with Charles here; so it follows that Charles will win any election conducted using a method satisfying the Condorcet criterion.
Hence under any voting method which satisfies the Condorcet criterion the winner will be the candidate preferred by the median voter. For binary decisions the majority vote satisfies the criterion; for multiway votes several methods satisfy it (see
Assume that there is an odd number of voters and at least two candidates, and assume that opinions are distributed along a spectrum. Assume that each voter ranks the candidates in an order of proximity such that the candidate closest to the voter receives their first preference, the next closest receives their second preference, and so forth. Then there is a median voter and we will show that the election will be won by the candidate who is closest to him or her.
Proof — Let the median voter be Marlene. The candidate who is closest to her will receive her first preference vote. Suppose that this candidate is Charles and that he lies to her left. Then Marlene and all voters to her left (comprising a majority of the electorate) will prefer Charles to all candidates to his right, and Marlene and all voters to her right will prefer Charles to all candidates to his left. ∎
The Condorcet criterion is defined as being satisfied by any voting method which ensures that a candidate who is preferred to every other candidate by a majority of the electorate will be the winner, and this is precisely the case with Charles here; so it follows that Charles will win any election conducted using a method satisfying the Condorcet criterion.
Hence under any voting method which satisfies the Condorcet criterion the winner will be the candidate preferred by the median voter. For binary decisions the majority vote satisfies the criterion; for multiway votes several methods satisfy it (see Condorcet method
A Condorcet method (; ) is an election method that elects the candidate who wins a majority of the vote in every head-to-head election against each of the other candidates, that is, a candidate preferred by more voters than any others, whenever ...
).
Assumptions
The theorem also applies when the number of voters is even, but the details depend on how ties are resolved. The assumption that preferences are cast in order of proximity can be relaxed to say merely that they are single-peaked. The assumption that opinions lie along a real line can be relaxed to allow more general topologies. ''Spatial / valence models:'' Suppose that each candidate has a '' valence'' (attractiveness) in addition to his or her position in space, and suppose that voter ''i'' ranks candidates ''j'' in decreasing order of ''vj'' – ''dij'' where ''vj'' is ''j'' 's valence and ''dij'' is the distance from ''i'' to ''j''. Then the median voter theorem still applies: Condorcet methods will elect the candidate voted for by the median voter.History
The theorem was first set out by Duncan Black in 1948. He wrote that he saw a large gap in economic theory concerning how voting determines the outcome of decisions, including political decisions. Black's paper triggered research on how economics can explain voting systems. In 1957Anthony Downs
Anthony Downs (November 21, 1930October 2, 2021) was an American economist specializing in public policy and public administration. His research focuses included political choice theory, rent control, affordable housing, and transportation econ ...
expounded upon the median voter theorem in his book ''An Economic Theory of Democracy''.Anthony Downs, "An Economic Theory of Democracy
''An Economic Theory of Democracy'' is a treatise of economics written by Anthony Downs, published in 1957. The book set forth a model with precise conditions under which economic theory could be applied to non-market political decision-making. ...
" (1957).
The median voter property
We will say that a voting method has the "median voter property in one dimension" if it always elects the candidate closest to the median voter under a one-dimensional spatial model. We may summarise the median voter theorem as saying that all Condorcet methods possess the median voter property in one dimension. It turns out that Condorcet methods are not unique in this:Coombs' method
Coombs' method or the Coombs ruleGrofman, Bernard, and Scott L. Feld (2004"If you like the alternative vote (a.k.a. the instant runoff), then you ought to know about the Coombs rule,"''Electoral Studies'' 23:641-59. is a ranked voting system whic ...
is not Condorcet-consistent but nonetheless satisfies the median voter property in one dimension.
Extension to distributions in more than one dimension
Gaussian
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below.
There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymo ...
, ''does'' have a median of this sort. Whenever the distribution of voters has a unique median in all directions, and voters rank candidates in order of proximity, the median voter theorem applies: the candidate closest to the median will have a majority preference over all his or her rivals, and will be elected by any voting method satisfying the median voter property in one dimension.See Valerio Dotti's thesi"Multidimensional Voting Models"
(2016). (Uniqueness here generalises the property guaranteed by oddness of sample size in a single dimension.) ''Proof''. See the diagram, in which the grey disc represents the voter distribution as uniform over a circle and M is the median in all directions. Let A and B be two candidates, of whom A is the closer to the median. Then the voters who rank A above B are precisely the ones to the left (i.e. the 'A' side) of the solid red line; and since A is closer than B to M, the median is also to the left of this line.
 Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B. ∎
It follows that all Condorcet methods – and also Coombs' – satisfy the median voter property in spaces of any dimension for voter distributions with omnidirectional medians.
It is easy to construct voter distributions which do not have a median in all directions. The simplest example consists of a distribution limited to 3 points not lying in a straight line, such as 1, 2 and 3 in the second diagram. Each voter location coincides with the median under a certain set of one-dimensional projections. If A, B and C are the candidates, then '1' will vote A-B-C, '2' will vote B-C-A, and '3' will vote C-A-B, giving a Condorcet cycle. This is the subject of the McKelvey–Schofield theorem.
Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B. ∎
It follows that all Condorcet methods – and also Coombs' – satisfy the median voter property in spaces of any dimension for voter distributions with omnidirectional medians.
It is easy to construct voter distributions which do not have a median in all directions. The simplest example consists of a distribution limited to 3 points not lying in a straight line, such as 1, 2 and 3 in the second diagram. Each voter location coincides with the median under a certain set of one-dimensional projections. If A, B and C are the candidates, then '1' will vote A-B-C, '2' will vote B-C-A, and '3' will vote C-A-B, giving a Condorcet cycle. This is the subject of the McKelvey–Schofield theorem.
Relation between the median in all directions and the geometric median
Whenever a unique omnidirectional median exists, it determines the result of Condorcet voting methods. At the same time thegeometric median
In geometry, the geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances ...
can be identified as the ideal winner of a ranked preference election (see Comparison of electoral systems
Electoral systems are the rules for conducting elections, a main component of which is the algorithm for determining the winner (or several winners) from the ballots cast. This article discusses methods and results of comparing different electora ...
). It is therefore important to know the relationship between the two. In fact whenever a median in all directions exists (at least for the case of discrete distributions), it coincides with the geometric median.
Hotelling's law
The more informal assertion – the median voter ''model'' – is related to Harold Hotelling's 'principle of minimum differentiation', also known as 'Hotelling's law
Hotelling's law is an observation in economics that in many markets it is rational for producers to make their products as similar as possible. This is also referred to as the principle of minimum differentiation as well as Hotelling's linear ci ...
'. It states that politicians gravitate toward the position occupied by the median voter, or more generally toward the position favored by the electoral system. It was first put forward (as an observation, without any claim to rigor) by Hotelling in 1929.
Hotelling saw the behavior of politicians through the eyes of an economist. He was struck by the fact that shops selling a particular good often congregate in the same part of a town, and saw this as analogous the convergence of political parties. In both cases it may be a rational policy for maximizing market share
Market share is the percentage of the total revenue or sales in a market that a company's business makes up. For example, if there are 50,000 units sold per year in a given industry, a company whose sales were 5,000 of those units would have a ...
.
As with any characterization of human motivation it depends on psychological factors which are not easily predictable, and is subject to many exceptions. It is also contingent on the voting system: politicians will not converge to the median voter unless the electoral process does so. If an electoral process gives more weight to rural than to urban voters, then parties are likely to converge to policies which favor rural areas rather than to the true median.
Uses of the median voter theorem
The theorem is valuable for the light it sheds on the optimality (and the limits to the optimality) of certain voting systems. Valerio Dotti points out broader areas of application:The ''Median Voter Theorem'' proved extremely popular in the Political Economy literature. The main reason is that it can be adopted to derive testable implications about the relationship between some characteristics of the voting population and the policy outcome, abstracting from other features of the political process.He adds that...
The median voter result has been applied to an incredible variety of questions. Examples are the analysis of the relationship between income inequality and size of governmental intervention in redistributive policies (Meltzer and Richard, 1981), the study of the determinants of immigration policies (Razin and Sadka, 1999), of the extent of taxation on different tyes of income (Bassetto and Benhabib, 2006),M. Bassetto and J. Benhabib, "Redistribution, Taxes, and the Median Voter" (2006). and many more.
See also
*Arrow's impossibility theorem
Arrow's impossibility theorem, the general possibility theorem or Arrow's paradox is an impossibility theorem in social choice theory that states that when voters have three or more distinct alternatives (options), no ranked voting electoral syste ...
* McKelvey–Schofield chaos theorem The McKelvey–Schofield chaos theorem is a result in social choice theory. It states that if preferences are defined over a multidimensional policy space, then majority rule is in general unstable: there is no Condorcet winner. Furthermore, any poi ...
* Median mechanism A median mechanism is a voting rule that allows people to decide on a value in a one-dimensional domain. Each person votes by writing down his/her ideal value, and the rule selects a single value which is (in the basic mechanism) the '' median'' of ...
* Ranked voting
The term ranked voting (also known as preferential voting or ranked choice voting) refers to any voting system in which voters ranking, rank their candidates (or options) in a sequence of first or second (or third, etc.) on their respective ball ...
References
Further reading
* * * * Dasgupta, Partha and Eric Maskin, "On the Robustness of Majority Rule", Journal of the European Economic Association, 2008. * * * * * * * * * * * {{cite journal , last=Waldfogel , first=Joel , title=The Median Voter and the Median Consumer: Local ''Private'' Goods and Population Composition , journal=Journal of Urban Economics
The ''Journal of Urban Economics'' is a bimonthly peer-reviewed academic journal covering urban economics. It is considered the premier journal in the field of urban economics. It was established in 1974 and is published by Elsevier. The editors-in ...
, year=2008 , volume=63 , issue=2 , pages=567–582 , doi=10.1016/j.jue.2007.04.002 , ssrn=878059
External link
The Median Voter Model
Political science theories Public choice theory Voting theory Game theory Mathematical economics