|
Meyer Wavelet
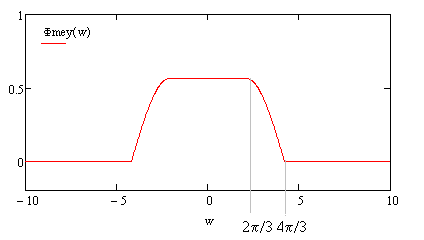
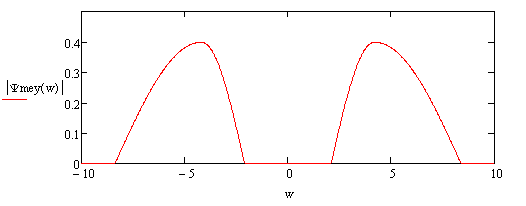
The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. As a type of a continuous wavelet, it has been applied in a number of cases, such as in adaptive filters, fractal random fields, and multi-fault classification. The Meyer wavelet is infinitely differentiable with infinite support and defined in frequency domain in terms of function \nu as : \Psi(\omega) := \begin \frac \sin\left(\frac \nu \left(\frac -1\right)\right) e^ & \text 2 \pi /3<, \omega, < 4 \pi /3, \\ \frac \cos\left(\frac \nu \left(\frac-1\right)\right) e^ & \text 4 \pi /3<, \omega, < 8 \pi /3, \\ 0 & \text, \end where : There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts : < ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectrum Meyer Wavelet
A spectrum (plural ''spectra'' or ''spectrums'') is a condition that is not limited to a specific set of values but can vary, without gaps, across a continuum. The word was first used scientifically in optics to describe the rainbow of colors in visible light after passing through a prism. As scientific understanding of light advanced, it came to apply to the entire electromagnetic spectrum. It thereby became a mapping of a range of magnitudes (wavelengths) to a range of qualities, which are the perceived "colors of the rainbow" and other properties which correspond to wavelengths that lie outside of the visible light spectrum. Spectrum has since been applied by analogy to topics outside optics. Thus, one might talk about the " spectrum of political opinion", or the "spectrum of activity" of a drug, or the "autism spectrum". In these uses, values within a spectrum may not be associated with precisely quantifiable numbers or definitions. Such uses imply a broad range of conditio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing. For example, a wavelet could be created to have a frequency of Middle C and a short duration of roughly one tenth of a second. If this wavelet were to be convolved with a signal created from the recording of a melody, then the resulting signal would be useful for determining when the Middle C note appeared in the song. Mathematically, a wavelet correlates with a signal if a portion of the signal is similar. Correlation is at the core of many practical wavelet applications. As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including but not limited to au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yves Meyer
Yves F. Meyer (; born 19 July 1939) is a French mathematician. He is among the progenitors of wavelet theory, having proposed the Meyer wavelet. Meyer was awarded the Abel Prize in 2017. Biography Born in Paris to a Jewish family, Yves Meyer studied at the Lycée Carnot in Tunis; he won the French General Student Competition (Concours Général) in Mathematics, and was placed first in the entrance examination for the École Normale Supérieure in 1957. He obtained his Ph.D. in 1966, under the supervision of Jean-Pierre Kahane. The Mexican historian Jean Meyer is his cousin. Yves Meyer taught at the Prytanée national militaire during his military service (1960–1963), then was a teaching assistant at the Université de Strasbourg (1963–1966), a professor at Université Paris-Sud (1966–1980), a professor at École Polytechnique (1980–1986), a professor at Université Paris-Dauphine (1985–1995), a senior researcher at the Centre national de la recherche scientifique ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Wavelet
{{Unreferenced, date=December 2009 In numerical analysis, continuous wavelets are functions used by the continuous wavelet transform. These functions are defined as analytical expressions, as functions either of time or of frequency. Most of the continuous wavelets are used for both wavelet decomposition and composition transforms. That is they are the continuous counterpart of orthogonal wavelets. The following continuous wavelets have been invented for various applications: * Poisson wavelet * Morlet wavelet * Modified Morlet wavelet * Mexican hat wavelet * Complex Mexican hat wavelet * Shannon wavelet * Meyer wavelet * Difference of Gaussians * Hermitian wavelet * Beta wavelet * Causal wavelet * μ wavelets * Cauchy wavelet * Addison wavelet See also *Wavelet A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function. Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal. As the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Fields
In physics and mathematics, a random field is a random function over an arbitrary domain (usually a multi-dimensional space such as \mathbb^n). That is, it is a function f(x) that takes on a random value at each point x \in \mathbb^n(or some other domain). It is also sometimes thought of as a synonym for a stochastic process with some restriction on its index set. That is, by modern definitions, a random field is a generalization of a stochastic process where the underlying parameter need no longer be real or integer valued "time" but can instead take values that are multidimensional vectors or points on some manifold. Formal definition Given a probability space (\Omega, \mathcal, P), an ''X''-valued random field is a collection of ''X''-valued random variables indexed by elements in a topological space ''T''. That is, a random field ''F'' is a collection : \ where each F_t is an ''X''-valued random variable. Examples In its discrete version, a random field is a list of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectrum Meyer Scalefunction
A spectrum (plural ''spectra'' or ''spectrums'') is a condition that is not limited to a specific set of values but can vary, without gaps, across a continuum. The word was first used scientifically in optics to describe the rainbow of colors in visible light after passing through a prism. As scientific understanding of light advanced, it came to apply to the entire electromagnetic spectrum. It thereby became a mapping of a range of magnitudes (wavelengths) to a range of qualities, which are the perceived "colors of the rainbow" and other properties which correspond to wavelengths that lie outside of the visible light spectrum. Spectrum has since been applied by analogy to topics outside optics. Thus, one might talk about the " spectrum of political opinion", or the "spectrum of activity" of a drug, or the "autism spectrum". In these uses, values within a spectrum may not be associated with precisely quantifiable numbers or definitions. Such uses imply a broad range of conditio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Domain
Time domain refers to the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various separate instants in the case of discrete time. An oscilloscope is a tool commonly used to visualize real-world signals in the time domain. A time-domain graph shows how a signal changes with time, whereas a frequency-domain graph shows how much of the signal lies within each given frequency band over a range of frequencies. Though most precisely referring to time in physics, the term ''time domain'' may occasionally informally refer to position in space when dealing with spatial frequencies, as a substitute for the more precise term ''spatial domain''. Origin of term The use of the contrasting terms ''time domain'' and '' frequency domain'' developed in U.S. communication engineering in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meyer Wavelet
The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. As a type of a continuous wavelet, it has been applied in a number of cases, such as in adaptive filters, fractal random fields, and multi-fault classification. The Meyer wavelet is infinitely differentiable with infinite support and defined in frequency domain in terms of function \nu as : \Psi(\omega) := \begin \frac \sin\left(\frac \nu \left(\frac -1\right)\right) e^ & \text 2 \pi /3<, \omega, < 4 \pi /3, \\ \frac \cos\left(\frac \nu \left(\frac-1\right)\right) e^ & \text 4 \pi /3<, \omega, < 8 \pi /3, \\ 0 & \text, \end where : There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts : < ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.gif)