Meyer wavelet on:
[Wikipedia]
[Google]
[Amazon]
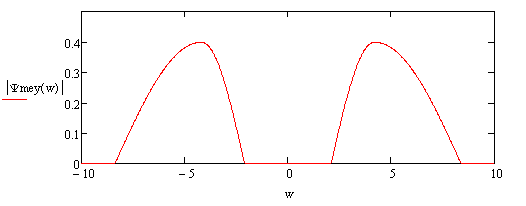 The Meyer wavelet is an orthogonal
The Meyer wavelet is an orthogonal 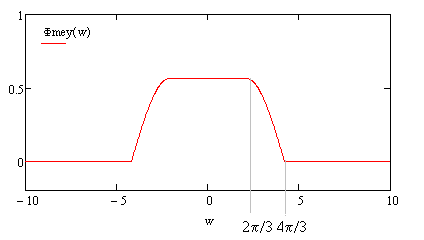 The Meyer scale function is given by
:
In the
The Meyer scale function is given by
:
In the 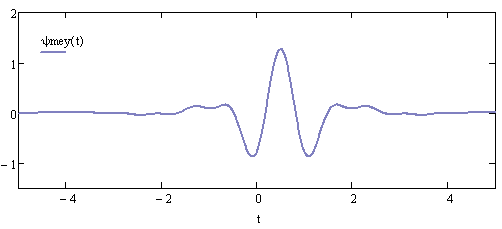
wavelet toolbox
Wavelets
 The Meyer wavelet is an orthogonal
The Meyer wavelet is an orthogonal wavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the num ...
proposed by Yves Meyer
Yves F. Meyer (; born 19 July 1939) is a French mathematician. He is among the progenitors of wavelet theory, having proposed the Meyer wavelet. Meyer was awarded the Abel Prize in 2017.
Biography
Born in Paris to a Jewish family, Yves Meyer ...
. As a type of a continuous wavelet
{{Unreferenced, date=December 2009
In numerical analysis, continuous wavelets are functions used by the continuous wavelet transform. These functions are defined as analytical expressions, as functions either of time or of frequency.
Most of the co ...
, it has been applied in a number of cases, such as in adaptive filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorit ...
s, fractal random fields In physics and mathematics, a random field is a random function over an arbitrary domain (usually a multi-dimensional space such as \mathbb^n). That is, it is a function f(x) that takes on a random value at each point x \in \mathbb^n(or some other ...
, and multi-fault classification.
The Meyer wavelet is infinitely differentiable with infinite support and defined in frequency domain in terms of function as
:
where
:
There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet.
For instance, another standard implementation adopts
:
 The Meyer scale function is given by
:
In the
The Meyer scale function is given by
:
In the time domain
Time domain refers to the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the c ...
, the waveform of the Meyer mother-wavelet has the shape as shown in the following figure:

Close expressions
Valenzuela and de Oliveira give the explicit expressions of Meyer wavelet and scale functions: : and : where : :References
*External links
{{commons, Wavelet, Waveletwavelet toolbox
Wavelets