|
Mermin–Peres Square
Quantum pseudo-telepathy is the fact that in certain Bayesian games with asymmetric information, players who have access to a shared physical system in an entangled quantum state, and who are able to execute strategies that are contingent upon measurements performed on the entangled physical system, are able to achieve higher expected payoffs in equilibrium than can be achieved in any mixed-strategy Nash equilibrium of the same game by players without access to the entangled quantum system. In their 1999 paper, Gilles Brassard, Richard Cleve and Alain Tapp demonstrated that quantum pseudo-telepathy allows players in some games to achieve outcomes that would otherwise only be possible if participants were allowed to communicate during the game. This phenomenon came to be referred to ''as quantum pseudo-telepathy'', with the prefix ''pseudo'' referring to the fact that quantum pseudo-telepathy does not involve the exchange of information between any parties. Instead, quantum pseu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Introduction To Quantum Mechanics
Quantum mechanics is the study of matter and its interactions with energy on the scale of atomic and subatomic particles. By contrast, classical physics explains matter and energy only on a scale familiar to human experience, including the behavior of astronomical bodies such as the moon. Classical physics is still used in much of modern science and technology. However, towards the end of the 19th century, scientists discovered phenomena in both the large ( macro) and the small ( micro) worlds that classical physics could not explain. The desire to resolve inconsistencies between observed phenomena and classical theory led to two major revolutions in physics that created a shift in the original scientific paradigm: the ''theory of relativity'' and the development of ''quantum mechanics''. This article describes how physicists discovered the limitations of classical physics and developed the main concepts of the quantum theory that replaced it in the early decades of the 20th c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
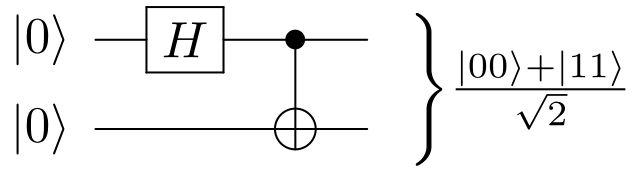
Bell State
The Bell states or EPR pairs are specific quantum states of two qubits that represent the simplest (and maximal) examples of quantum entanglement; conceptually, they fall under the study of quantum information science. The Bell states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particle being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell state the two qubits are in initially. Bell states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for 3 or more subsystems. Under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Number
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as-is. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Coloring Game
The graph coloring game is a mathematical game related to graph theory. Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. In a coloring game, two players use a given set of colors to construct a coloring of a graph, following specific rules depending on the game we consider. One player tries to successfully complete the coloring of the graph, when the other one tries to prevent him from achieving it. Vertex coloring game The vertex coloring game was introduced in 1981 by Brams and rediscovered ten years after by Bodlaender. Its rules are as follows: # Alice and Bob color the vertices of a graph ''G'' with a set ''k'' of colors. # Alice and Bob take turns, coloring properly an uncolored vertex (in the standard version, Alice begins). # If a vertex ''v'' is impossible to color properly (for any color, ''v'' has a neighbor colored with it), then Bob wins. # If the graph is completely colored, then Alice wins. The game chromatic numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
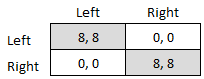
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-equilibrium combinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Over A Field
In mathematics, an algebra over a field (often simply called an algebra) is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition and scalar multiplication by elements of a field and satisfying the axioms implied by "vector space" and "bilinear". The multiplication operation in an algebra may or may not be associative, leading to the notions of associative algebras and non-associative algebras. Given an integer ''n'', the ring of real square matrices of order ''n'' is an example of an associative algebra over the field of real numbers under matrix addition and matrix multiplication since matrix multiplication is associative. Three-dimensional Euclidean space with multiplication given by the vector cross product is an example of a nonassociative algebra over the field of real numbers since the vector cross product is nonassociative, satisfying the Jacobi identity i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asher Peres
Asher Peres ( he, אשר פרס; January 30, 1934 – January 1, 2005) was an Israeli physicist. He is well known for his work relating quantum mechanics and information theory. He helped to develop the Peres–Horodecki criterion for quantum entanglement, as well as the concept of quantum teleportation, and collaborated with others on quantum information and special relativity. He also introduced the Peres metric and researched the Hamilton–Jacobi–Einstein equation in general relativity. With Mario Feingold, he published work in quantum chaos that is known to mathematicians as the Feingold–Peres conjecture and to physicists as the Feingold–Peres theory. Life According to his autobiography, he was born ''Aristide Pressman'' in Beaulieu-sur-Dordogne in France, where his father, a Polish electrical engineer, had found work laying down power lines. He was given the name ''Aristide'' at birth, because the name his parents wanted, ''Asher'', the name of his maternal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Mermin
Nathaniel David Mermin (; born 30 March 1935) is a solid-state physicist at Cornell University best known for the eponymous Mermin–Wagner theorem, his application of the term " boojum" to superfluidity, his textbook with Neil Ashcroft on solid-state physics, and for contributions to the foundations of quantum mechanics and quantum information science. Education and career Mermin was born in 1935 in New Haven, Connecticut. He obtained a bachelor's degree in mathematics from Harvard University in 1956, graduating ''summa cum laude.'' He remained at Harvard for his graduate studies, earning a PhD in physics in 1961. After holding postdoctoral positions at the University of Birmingham and the University of California, San Diego, he joined the Cornell University faculty in 1964. He became a Cornell professor emeritus in 2006. Early in his career, Mermin worked in statistical physics and condensed-matter physics, including the study of matter at low temperatures, the behavior of e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of the property that says something like or , the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it (for example, ); such operations are ''not'' commutative, and so are referred to as ''noncommutative operations''. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A similar property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Matrices
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () when used in connection with isospin symmetries. \begin \sigma_1 = \sigma_\mathrm &= \begin 0&1\\ 1&0 \end \\ \sigma_2 = \sigma_\mathrm &= \begin 0& -i \\ i&0 \end \\ \sigma_3 = \sigma_\mathrm &= \begin 1&0\\ 0&-1 \end \\ \end These matrices are named after the physicist Wolfgang Pauli. In quantum mechanics, they occur in the Pauli equation which takes into account the interaction of the spin of a particle with an external electromagnetic field. They also represent the interaction states of two polarization filters for horizontal/vertical polarization, 45 degree polarization (right/left), and circular polarization (right/left). Each Pauli matrix is Hermitian, and together with the iden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |