|
Laplacian Matrix
In the mathematical field of graph theory, the Laplacian matrix, also called the graph Laplacian, admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. Named after Pierre-Simon Laplace, the graph Laplacian matrix can be viewed as a matrix form of the negative discrete Laplace operator on a graph approximating the negative continuous Laplacian obtained by the finite difference method. The Laplacian matrix relates to many useful properties of a graph. Together with Kirchhoff's theorem, it can be used to calculate the number of spanning trees for a given graph. The sparsest cut of a graph can be approximated through the Fiedler vector — the eigenvector corresponding to the second smallest eigenvalue of the graph Laplacian — as established by Cheeger's inequality. The spectral decomposition of the Laplacian matrix allows constructing low dimensional embeddings that appear in many machine learning applications and determines a spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dimensionality Reduction
Nonlinear dimensionality reduction, also known as manifold learning, refers to various related techniques that aim to project high-dimensional data onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping (either from the high-dimensional space to the low-dimensional embedding or vice versa) itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis. Applications of NLDR Consider a dataset represented as a matrix (or a database table), such that each row represents a set of attributes (or features or dimensions) that describe a particular instance of something. If the number of attributes is large, then the space of unique possible rows is exponentially large. Thus, the larger the dimensionality, the more difficult it becomes to sample the space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Matrix
In the mathematical field of algebraic graph theory, the degree matrix of an undirected graph is a diagonal matrix which contains information about the degree of each vertex—that is, the number of edges attached to each vertex.. It is used together with the adjacency matrix to construct the Laplacian matrix of a graph: the Laplacian matrix is the difference of the degree matrix and the adjacency matrix.. Definition Given a graph G=(V,E) with , V, =n, the degree matrix D for G is a n \times n diagonal matrix defined as :D_:=\left\{ \begin{matrix} \deg(v_i) & \mbox{if}\ i = j \\ 0 & \mbox{otherwise} \end{matrix} \right. where the degree \deg(v_i) of a vertex counts the number of times an edge terminates at that vertex. In an undirected graph, this means that each loop increases the degree of a vertex by two. In a directed graph, the term ''degree'' may refer either to indegree (the number of incoming edges at each vertex) or outdegree (the number of outgoing edges at each vertex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Graph Theory
In mathematics, spectral graph theory is the study of the properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph, such as its adjacency matrix or Laplacian matrix. The adjacency matrix of a simple undirected graph is a real symmetric matrix and is therefore orthogonally diagonalizable; its eigenvalues are real algebraic integers. While the adjacency matrix depends on the vertex labeling, its spectrum is a graph invariant, although not a complete one. Spectral graph theory is also concerned with graph parameters that are defined via multiplicities of eigenvalues of matrices associated to the graph, such as the Colin de Verdière number. Cospectral graphs Two graphs are called cospectral or isospectral if the adjacency matrices of the graphs are isospectral, that is, if the adjacency matrices have equal multisets of eigenvalues. Cospectral graphs need not be isomorphic, but isomorphic graphs a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected (i.e. all of its edges are bidirectional), the adjacency matrix is symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are incident or not, and its degree matrix, which contains information about the degree of each vertex. Definition For a simple graph with vertex set , the adjacency matrix is a square matrix such that its element is one when there is an edge from vertex to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glossary Of Graph Theory
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges. Symbols A B C D E F G H I K L M N O ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Graph
In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called '' vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave
A sine wave, sinusoidal wave, or just sinusoid is a curve, mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph of a function, graph. It is a type of continuous wave and also a Smoothness, smooth periodic function. It occurs often in mathematics, as well as in physics, engineering, signal processing and many other fields. Formulation Its most basic form as a function of time (''t'') is: y(t) = A\sin(2 \pi f t + \varphi) = A\sin(\omega t + \varphi) where: * ''A'', ''amplitude'', the peak deviation of the function from zero. * ''f'', ''frequency, ordinary frequency'', the ''Real number, number'' of oscillations (cycles) that occur each second of time. * ''ω'' = 2''f'', ''angular frequency'', the rate of change of the function argument in units of radians per second. * \varphi, ''phase (waves), phase'', specifies (in radians) where in its cycle the oscillation is at ''t'' = 0. When \varphi is non-zero, the entire waveform appears to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Fourier Transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced samples of a function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex-valued function of frequency. The interval at which the DTFT is sampled is the reciprocal of the duration of the input sequence. An inverse DFT is a Fourier series, using the DTFT samples as coefficients of complex sinusoids at the corresponding DTFT frequencies. It has the same sample-values as the original input sequence. The DFT is therefore said to be a frequency domain representation of the original input sequence. If the original sequence spans all the non-zero values of a function, its DTFT is continuous (and periodic), and the DFT provides discrete samples of one cycle. If the original sequence is one cycle of a periodic function, the DFT provides all the non-zero values of one DTFT cycle. The DFT is the most important discret ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Fourier Transform
In mathematics, the graph Fourier transform is a mathematical transform which eigendecomposes the Laplacian matrix of a graph into eigenvalues and eigenvectors. Analogously to the classical Fourier Transform, the eigenvalues represent frequencies and eigenvectors form what is known as a graph Fourier basis. The Graph Fourier transform is important in spectral graph theory. It is widely applied in the recent study of graph structured learning algorithms, such as the widely employed convolutional networks. Definition Given an undirected weighted graph G = (V,E), where V is the set of nodes with , V, = N (N being the number of nodes) and E is the set of edges, a graph signal f: V \rightarrow \mathbb is a function defined on the vertices of the graph G. The signal f maps every vertex \_ to a real number f(i). Any graph signal can be projected on the eigenvectors of the Laplacian matrix L. Let \lambda_l and \mu_l be the l_\text eigenvalue and eigenvector of the Laplacian matrix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
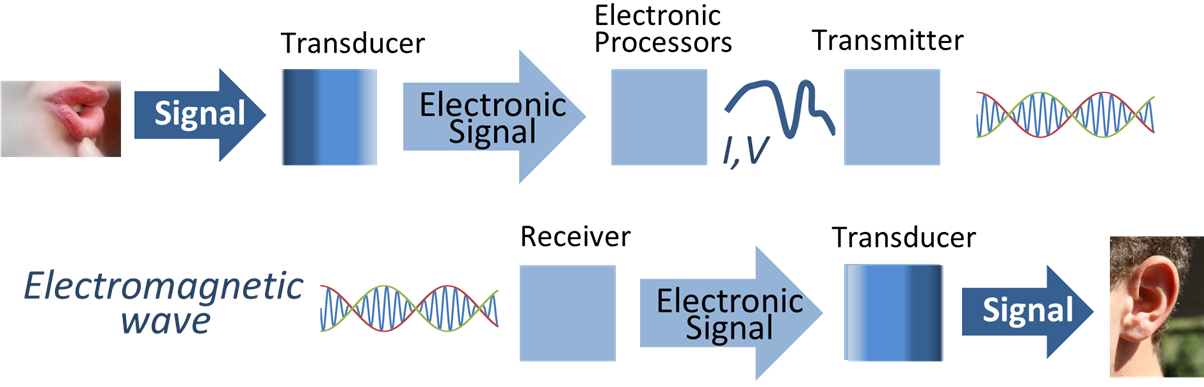
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |