|
Lawrence Shepp
Lawrence Alan Shepp (September 9, 1936 Brooklyn, NY – April 23, 2013, Tucson, AZ) was an American mathematician, specializing in statistics and computational tomography. Shepp obtained his PhD from Princeton University in 1961 with a dissertation entitled ''Recurrent Sums of Random Variables''. His advisor was William Feller. He joined Bell Laboratories in 1962. He joined Rutgers University in 1997. He joined University of Pennsylvania in 2010. His work in tomography has had biomedical imaging applications, and he has also worked as professor of radiology at Columbia University (1973–1996), as a mathematician in the radiology service of Columbia Presbyterian Hospital. Awards and honors * 2014: IEEE Marie Sklodowska-Curie Award * 2012: Became a fellow of the American Mathematical Society. * 1992: Elected member of the Institute of Medicine * 1989: Elected member of the National Academy of Sciences * 1979: IEEE Distinguished Scientist Award in 1979 * 1979: Lester R. For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brooklyn, NY
Brooklyn () is a Boroughs of New York City, borough of New York City, coextensive with Kings County, in the U.S. state of New York (state), New York. Kings County is the most populous Administrative divisions of New York (state)#County, county in the State of New York, and the County statistics of the United States#Most densely populated, second-most densely populated county in the United States, behind New York County (Manhattan). Brooklyn is also New York City's most populous borough,2010 Gazetteer for New York State United States Census Bureau. Retrieved September 18, 2016. with 2,736,074 residents in 2020. Named after the Dutch village of Breukelen, Brooklyn is located on the western portion of Long Island and shares a border with the borough of Queens. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Kruskal
Joseph Bernard Kruskal, Jr. (; January 29, 1928 – September 19, 2010) was an American mathematician, statistician, computer scientist and psychometrician. Personal life Kruskal was born to a Jewish family in New York City to a successful fur wholesaler, Joseph B. Kruskal, Sr. His mother, Lillian Rose Vorhaus Kruskal Oppenheimer, became a noted promoter of origami during the early era of television. Kruskal had two notable brothers, Martin David Kruskal, co-inventor of solitons, and William Kruskal, who developed the Kruskal–Wallis one-way analysis of variance. One of Joseph Kruskal's nephews is notable computer scientist and professor Clyde Kruskal. Education and career He was a student at the University of Chicago earning a bachelor of science in mathematics in the year of 1948, and a master of science in mathematics in the following year 1949. After his time at the University of Chicago Kruskal attended Princeton University, where he completed his Ph.D. in 1954, nomina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rutgers University Faculty
This is an enumeration of notable people affiliated with Rutgers University, including graduates of the undergraduate and graduate and professional programs at all three campuses, former students who did not graduate or receive their degree, presidents of the university, current and former professors, as well as members of the board of trustees and board of governors, and coaches affiliated with the university's athletic program. Also included are characters in works of fiction (books, films, television shows, et cetera) who have been mentioned or were depicted as having an affiliation with Rutgers, either as a student, alumnus, or member of the faculty. Some noted alumni and faculty may be also listed in the main Rutgers University article or in some of the affiliated articles. Individuals are sorted by category and alphabetized within each category. Default campus for listings is the New Brunswick campus, the systems' largest campus, with Camden and Newark campus affiliat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Princeton University Alumni
Princeton University is a private research university in Princeton, New Jersey. Founded in 1746 in Elizabeth as the College of New Jersey, Princeton is the fourth-oldest institution of higher education in the United States and one of the nine colonial colleges chartered before the American Revolution. It is one of the highest-ranked universities in the world. The institution moved to Newark in 1747, and then to the current site nine years later. It officially became a university in 1896 and was subsequently renamed Princeton University. It is a member of the Ivy League. The university is governed by the Trustees of Princeton University and has an endowment of $37.7 billion, the largest endowment per student in the United States. Princeton provides undergraduate and graduate instruction in the humanities, social sciences, natural sciences, and engineering to approximately 8,500 students on its main campus. It offers postgraduate degrees through the Princeton School of Publi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ridge Function
In mathematics, a ridge function is any function f:\R^d\rightarrow\R that can be written as the composition of a univariate function with an affine transformation, that is: f(\boldsymbol) = g(\boldsymbol\cdot \boldsymbol) for some g:\R\rightarrow\R and \boldsymbol\in\R^d. Coinage of the term 'ridge function' is often attributed to B.F. Logan and L.A. Shepp. Relevance A ridge function is not susceptible to the curse of dimensionality, making it an instrumental tool in various estimation problems. This is a direct result of the fact that ridge functions are constant in d-1 directions: Let a_1,\dots,a_ be d-1 independent vectors that are orthogonal to a, such that these vectors span d-1 dimensions. Then : f\left(\boldsymbol + \sum_^c_k\boldsymbol_k\right)=g\left(\boldsymbol\cdot\boldsymbol + \sum_^ c_k\boldsymbol_k\cdot\boldsymbol\right)=g\left(\boldsymbol\cdot\boldsymbol + \sum_^ c_k0\right) = g(\boldsymbol \cdot \boldsymbol)=f(\boldsymbol) for all c_i\in\R,1\le i [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Estimator
In statistics, sieve estimators are a class of non-parametric estimators which use progressively more complex models to estimate an unknown high-dimensional function as more data becomes available, with the aim of asymptotically reducing error towards zero as the amount of data increases. This method is generally attributed to Ulf Grenander. Method of sieves in Positron emission tomography Sieve estimators have been used extensively for estimating density functions in high-dimensional spaces such as in Positron emission tomography(PET). The first exploitation of Sieves in PET for solving the maximum-likelihood Positron emission tomography#Image reconstruction problem was by Donald Snyder and Michael Miller, where they stabilized the time-of-flight PET problem originally solved by Shepp and Vardi. Shepp and Vardi's introduction of Maximum-likelihood estimators in emission tomography exploited the use of the Expectation-Maximization algorithm, which as it ascended towards the maxim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Parking Problem
The parallel parking problem is a motion planning problem in control theory and mechanics to determine the path a car must take to parallel park into a parking space. The front wheels of a car are permitted to turn, but the rear wheels must stay aligned. When a car is initially adjacent to a parking space, to move into the space it would need to move in a direction perpendicular to the allowed path of motion of the rear wheels. The admissible motions of the car in its configuration space are an example of a nonholonomic system. See also * Automatic parking * Bicycle and motorcycle dynamics * Falling cat problem * Moving sofa problem In mathematics, the moving sofa problem or sofa problem is a two-dimensional idealisation of real-life furniture-moving problems and asks for the rigid two-dimensional shape of largest area that can be maneuvered through an L-shaped planar region ... References * . * . Control theory {{applied-math-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
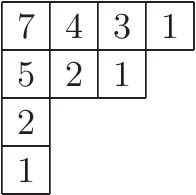
Hook Length Formula
In combinatorial mathematics, the hook length formula is a formula for the number of standard Young tableaux whose shape is a given Young diagram. It has applications in diverse areas such as representation theory, probability, and algorithm analysis; for example, the problem of longest increasing subsequences. A related formula gives the number of semi-standard Young tableaux, which is a specialization of a Schur polynomial. Definitions and statement Let \lambda=(\lambda_1\geq \cdots\geq \lambda_k) be a partition of n=\lambda_1+\cdots+\lambda_k. It is customary to interpret \lambda graphically as a Young diagram, namely a left-justified array of square cells with k rows of lengths \lambda_1,\ldots,\lambda_k. A (standard) Young tableau of shape \lambda is a filling of the n cells of the Young diagram with all the integers \, with no repetition, such that each row and each column form increasing sequences. For the cell in position (i,j), in the ith row and jth column, the hook H_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dubins Path
In geometry, the term Dubins path typically refers to the shortest curve that connects two points in the two-dimensional Euclidean plane (i.e. ''x-y'' plane) with a constraint on the curvature of the path and with prescribed initial and terminal tangents to the path, and an assumption that the vehicle traveling the path can only travel forward. If the vehicle can also travel in reverse, then the path follows the Reeds–Shepp curve. In 1957, Lester Eli Dubins (1920–2010) proved using tools from analysis that any such path will consist of maximum curvature and/or straight line segments. In other words, the shortest path will be made by joining circular arcs of maximum curvature and straight lines. In 1974 Harold H. Johnson proved Dubins' result by applying Pontryagin's maximum principle. In particular, Harold H. Johnson presented necessary and sufficient conditions for a plane curve, which has bounded piecewise continuous curvature and prescribed initial and terminal points and di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Tomography
Discrete tomography Herman, G. T. and Kuba, A., Discrete Tomography: Foundations, Algorithms, and Applications, Birkhäuser Boston, 1999 Herman, G. T. and Kuba, A., Advances in Discrete Tomography and Its Applications, Birkhäuser Boston, 2007 focuses on the problem of reconstruction of binary images (or finite subsets of the integer lattice) from a small number of their projections. In general, tomography deals with the problem of determining shape and dimensional information of an object from a set of projections. From the mathematical point of view, the object corresponds to a function and the problem posed is to reconstruct this function from its integrals or sums over subsets of its domain. In general, the tomographic inversion problem may be continuous or discrete. In continuous tomography both the domain and the range of the function are continuous and line integrals are used. In discrete tomography the domain of the function may be either discrete or continuous, and the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coupon Collector's Problem
In probability theory, the coupon collector's problem describes "collect all coupons and win" contests. It asks the following question: If each box of a brand of cereals contains a coupon, and there are ''n'' different types of coupons, what is the probability that more than ''t'' boxes need to be bought to collect all ''n'' coupons? An alternative statement is: Given ''n'' coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once? The mathematical analysis of the problem reveals that the expected number of trials needed grows as \Theta(n\log(n)). For example, when ''n'' = 50 it takes about 225E(50) = 50(1 + 1/2 + 1/3 + ... + 1/50) = 224.9603, the expected number of trials to collect all 50 coupons. The approximation n\log n+\gamma n+1/2 for this expected number gives in this case 50\log 50+50\gamma+1/2 \approx 195.6011+28.8608+0.5\approx 224.9619. trials on average to collect all 50 coupons. Solution Calcula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |