|
Khazeni, Abolfath
Abū al-Fath Abd al-Rahman Mansūr al-Khāzini or simply al-Khāzini (, flourished 1115–1130) was an Iranian astronomer of Greek origin from Seljuk Persia. His astronomical tables written under the patronage of Sultan Sanjar (', 1115) is considered to be one of the major works in mathematical astronomy of the medieval period. Montelle, C. (2011). The ‘Well-Known Calendars’: Al-Khāzinī’s Description of Significant Chronological Systems for Medieval Mathematical Astronomy in Arabic. In Steele J. (Ed.), Calendars and Years II: Astronomy and Time in the Ancient and Medieval World (pp. 107-126). Oxford; Oakville: Oxbow Books. He provided the positions of fixed stars, and for oblique ascensions and time-equations for the latitude of Marv in which he was based.Meyerhof, M. (1948). 'Alī al-Bayhaqī's Tatimmat Siwān al-Hikma: A Biographical Work on Learned Men of the Islam. Osiris, 8, 122-217. He also wrote extensively on various calendrical systems and on the various mani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Islamic Science
Science in the medieval Islamic world was the science developed and practised during the Islamic Golden Age under the Umayyads of Córdoba, the Abbadids of Seville, the Samanids, the Ziyarids, the Buyids in Persia, the Abbasid Caliphate and beyond, spanning the period roughly between 786 and 1258. Islamic scientific achievements encompassed a wide range of subject areas, especially astronomy, mathematics, and medicine. Other subjects of scientific inquiry included alchemy and chemistry, botany and agronomy, geography and cartography, ophthalmology, pharmacology, physics, and zoology. Medieval Islamic science had practical purposes as well as the goal of understanding. For example, astronomy was useful for determining the ''Qibla'', the direction in which to pray, botany had practical application in agriculture, as in the works of Ibn Bassal and Ibn al-'Awwam, and geography enabled Abu Zayd al-Balkhi to make accurate maps. Islamic mathematicians such as Al-Khwarizmi, Avicenn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Astronomy
Theoretical astronomy is the use of analytical and computational models based on principles from physics and chemistry to describe and explain astronomical objects and astronomical phenomena. Theorists in astronomy endeavor to create theoretical models and from the results predict observational consequences of those models. The observation of a phenomenon predicted by a model allows astronomers to select between several alternate or conflicting models as the one best able to describe the phenomena. Ptolemy's ''Almagest'', although a brilliant treatise on theoretical astronomy combined with a practical handbook for computation, nevertheless includes compromises to reconcile discordant observations with a geocentric model. Modern theoretical astronomy is usually assumed to have begun with the work of Johannes Kepler (1571–1630), particularly with Kepler's laws. The history of the descriptive and theoretical aspects of the Solar System mostly spans from the late sixteenth century t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alchemists Of The Medieval Islamic World
Alchemy (from Arabic: ''al-kīmiyā''; from Ancient Greek: χυμεία, ''khumeía'') is an ancient branch of natural philosophy, a philosophical and protoscientific tradition that was historically practiced in China, India, the Muslim world, and Europe. In its Western form, alchemy is first attested in a number of pseudepigraphical texts written in Greco-Roman Egypt during the first few centuries AD.Principe, Lawrence M. The secrets of alchemy'. University of Chicago Press, 2012, pp. 9–14. Alchemists attempted to purify, mature, and perfect certain materials. Common aims were chrysopoeia, the transmutation of "base metals" (e.g., lead) into "noble metals" (particularly gold); the creation of an elixir of immortality; and the creation of panaceas able to cure any disease. The perfection of the human body and soul was thought to result from the alchemical ''magnum opus'' ("Great Work"). The concept of creating the philosophers' stone was variously connected with all of these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Islamic Philosophers
Muslim philosophers both profess Islam and engage in a style of philosophy situated within the structure of the Arabic language and Islam, though not necessarily concerned with religious issues. The sayings of the companions of Muhammad contained little philosophical discussion. In the eighth century, extensive contact with the Byzantine Empire led to a drive to translate philosophical works of Ancient Greek Philosophy (especially the texts of Aristotle) into Arabic. The ninth-century Al-Kindi is considered the founder of Islamic peripatetic philosophy (800–1200)./ref> , - , Averroes , , Spain (Andalusia) , 1126–1198 , Peripatetic , Being described as "founding father of secular thought in Western Europe", He was known by the nickname ''the Commentator'' for his precious commentaries on Aristotle's works. His main work was ''The Incoherence of the Incoherence'' in which he defended philosophy against al-Ghazali's claims in ''The Incoherence of the Philosophers''. His other wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12th-century Iranian Mathematicians
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12th-century Iranian Astronomers
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12th-century Alchemists
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dinar
The dinar () is the principal currency unit in several countries near the Mediterranean Sea, and its historical use is even more widespread. The modern dinar's historical antecedents are the gold dinar and the silver dirham, the main coin of the medieval Islamic empires, first issued in AH 77 (696–697 CE) by Caliph Abd al-Malik ibn Marwan. The word "dinar" derives from the Latin " ''dēnārius''," a silver coin of ancient Rome, which was first minted about c.211 BCE. The English word "dinar" is the transliteration of the Arabic دينار (''dīnār''), which was borrowed via the Syriac ''dīnarā'', itself from the Latin ''dēnārius''. The Kushan Empire introduced a gold coin known as the ''dīnāra'' into India in the 1st century AD; the Gupta Empire and its successors up to the 6th century adopted the coin. The modern gold dinar is a projected bullion gold coin, not issued as official currency by any state. Legal tender Countries currently usi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oneworld Publications
Oneworld Publications is a British independent publishing firm founded in 1986 by Novin Doostdar and Juliet Mabey originally to publish accessible non-fiction by experts and academics for the general market."About Us" Oneworld Publications. Based in , it later added a literary fiction list (in 2009) and both a children's list (Rock the Boat, 2015) and an upmarket crime list (Point Blank, 2016), and now publishes across a wide range of subjects, including history, politics, current affairs, popular science, religion, philosophy, and psychology, as well as literary fiction, crime fiction and suspense, and children's titles. A large proportion of Oneworld fiction across all its lists is translated. Among the writers on th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jalali Calendar
The Jalali calendar is a solar calendar, was compiled during the reign of Jalaluddin Malik-Shah I of Seljuk by the order of Nizam al-Mulk and the place of observation were the cities of Isfahan (the capital of the Seljuks), Rey, and Nishapur. Variants of the Jalali calendar are still in use today in Iran and Afghanistan. In Iran, the Persian names of the zodiac are used while in Afghanistan the original Arabic names are used. It gains approximately 1 day on the Julian calendar every 128 years. The tropical Jalali calendar ( fa, گاهشماری جلالی or تقویم جلالی), which inherited some aspects from the Yazdgerdi calendar, was adopted on 15 March 1079 by the Seljuk Sultan Jalal al-Din Malik Shah I (for whom it was named), based on the recommendations of a committee of astronomers, including Omar Khayyam, at the imperial observatory in his capital city of Isfahan. Month computations were based on solar transits through the zodiac. It remained in use for eight ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greater Khorasan
Greater Khorāsān,Dabeersiaghi, Commentary on Safarnâma-e Nâsir Khusraw, 6th Ed. Tehran, Zavvâr: 1375 (Solar Hijri Calendar) 235–236 or Khorāsān ( pal, Xwarāsān; fa, خراسان ), is a historical eastern region in the Iranian Plateau between Western and Central Asia. The name ''Khorāsān'' is Persian and means "where the sun arrives from" or "the Eastern Province".Sykes, M. (1914). "Khorasan: The Eastern Province of Persia". ''Journal of the Royal Society of Arts'', 62(3196), 279-286.A compound of ''khwar'' (meaning "sun") and ''āsān'' (from ''āyān'', literally meaning "to come" or "coming" or "about to come"). Thus the name ''Khorasan'' (or ''Khorāyān'' ) means "sunrise", viz. " Orient, East"Humbach, Helmut, and Djelani Davari, "Nāmé Xorāsān", Johannes Gutenberg-Universität Mainz; Persian translation by Djelani Davari, published in Iranian Languages Studies Website. MacKenzie, D. (1971). ''A Concise Pahlavi Dictionary'' (p. 95). London: Oxford University ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
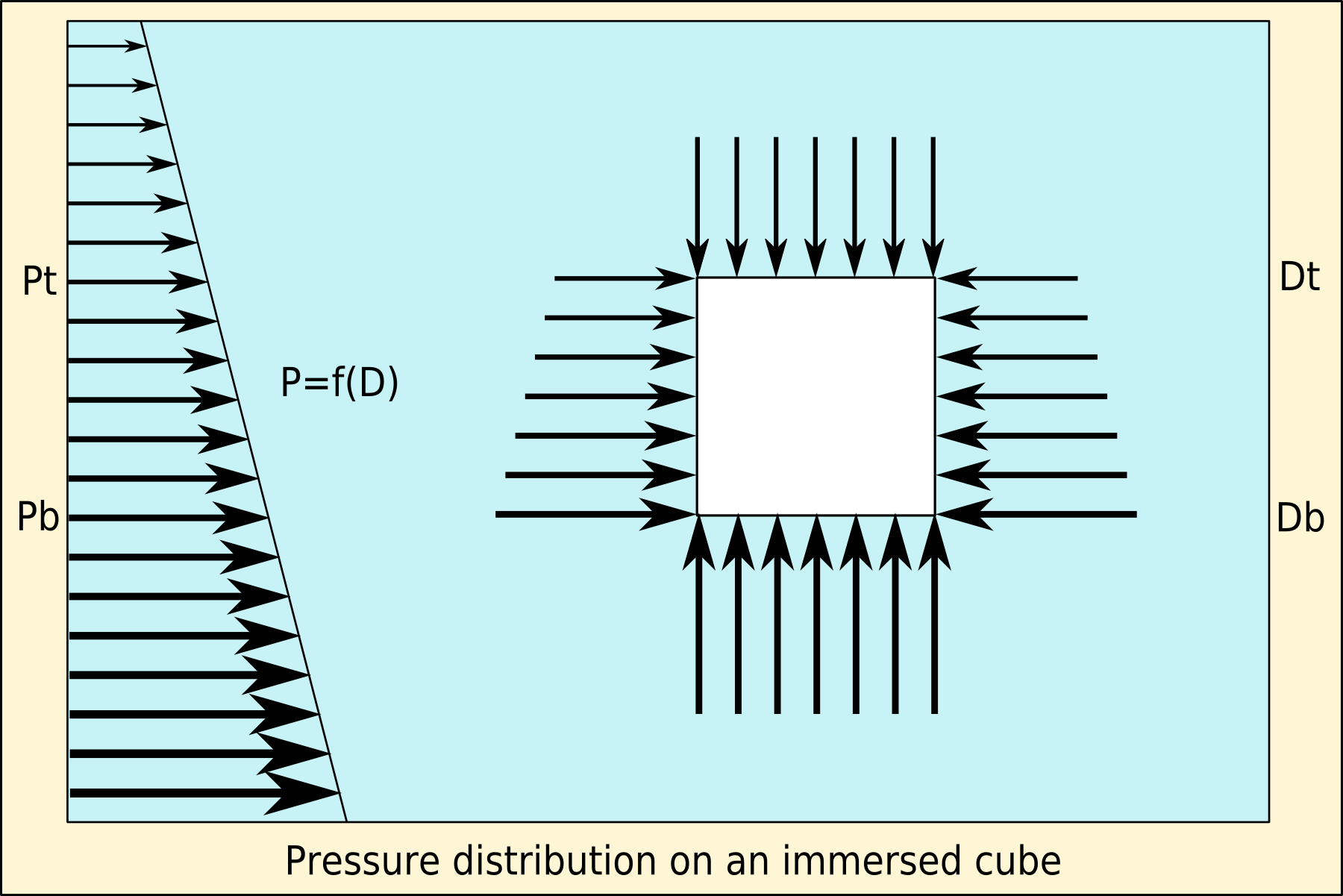
Archimedes' Principle
Archimedes' principle (also spelled Archimedes's principle) states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse. Explanation In ''On Floating Bodies'', Archimedes suggested that (c. 246 BC): Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |