|
Jacobi Elliptic Cosine
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum (see also pendulum (mathematics)), as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation \operatorname for \sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by . Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later. Overview There are twelve Jacobi elliptic fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Torus
In mathematics, a complex torus is a particular kind of complex manifold ''M'' whose underlying smooth manifold is a torus in the usual sense (i.e. the cartesian product of some number ''N'' circles). Here ''N'' must be the even number 2''n'', where ''n'' is the complex dimension of ''M''. All such complex structures can be obtained as follows: take a lattice Λ in a vector space V isomorphic to C''n'' considered as real vector space; then the quotient group V/\Lambda is a compact complex manifold. All complex tori, up to isomorphism, are obtained in this way. For ''n'' = 1 this is the classical period lattice construction of elliptic curves. For ''n'' > 1 Bernhard Riemann found necessary and sufficient conditions for a complex torus to be an algebraic variety; those that are varieties can be embedded into complex projective space, and are the abelian varieties. The actual projective embeddings are complicated (see equations defining abelian varieties) when ''n'' > 1, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which it is initially defined becomes divergent. The step-wise continuation technique may, however, come up against difficulties. These may have an essentially topological nature, leading to inconsistencies (defining more than one value). They may alternatively have to do with the presence of singularities. The case of several complex variables is rather different, since singularities then need not be isolated points, and its investigation was a major reason for the development of sheaf cohomology. Initial discussion Suppose ''f'' is an analytic function defined on a non-empty open subset ''U'' of the complex plane If ''V'' is a larger open subset of containing ''U'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and interior. Intuitively speaking, a neighbourhood of a point is a set of points containing that point where one can move some amount in any direction away from that point without leaving the set. Definitions Neighbourhood of a point If X is a topological space and p is a point in X, then a of p is a subset V of X that includes an open set U containing p, p \in U \subseteq V \subseteq X. This is also equivalent to the point p \in X belonging to the topological interior of V in X. The neighbourhood V need be an open subset X, but when V is open in X then it is called an . Some authors have been known to require neighbourhoods to be open, so it is important to note conventions. A set that is a neighbourhood of each of its points is open since it can be expressed as the union of open ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meromorphic Function
In the mathematical field of complex analysis, a meromorphic function on an open subset ''D'' of the complex plane is a function that is holomorphic on all of ''D'' ''except'' for a set of isolated points, which are poles of the function. The term comes from the Greek ''meros'' ( μέρος), meaning "part". Every meromorphic function on ''D'' can be expressed as the ratio between two holomorphic functions (with the denominator not constant 0) defined on ''D'': any pole must coincide with a zero of the denominator. Heuristic description Intuitively, a meromorphic function is a ratio of two well-behaved (holomorphic) functions. Such a function will still be well-behaved, except possibly at the points where the denominator of the fraction is zero. If the denominator has a zero at ''z'' and the numerator does not, then the value of the function will approach infinity; if both parts have a zero at ''z'', then one must compare the multiplicity of these zeros. From an algebr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if its Taylor series about ''x''0 converges to the function in some neighborhood for every ''x''0 in its domain. Definitions Formally, a function f is ''real analytic'' on an open set D in the real line if for any x_0\in D one can write : f(x) = \sum_^\infty a_ \left( x-x_0 \right)^ = a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + a_3 (x-x_0)^3 + \cdots in which the coefficients a_0, a_1, \dots are real numbers and the series is convergent to f(x) for x in a neighborhood of x_0. Alternatively, a real analytic function is an infinitely differentiable function such that the Taylor series at any point x_0 in its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch Point
In the mathematical field of complex analysis, a branch point of a multi-valued function (usually referred to as a "multifunction" in the context of complex analysis) is a point such that if the function is n-valued (has n values) at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept. Branch points fall into three broad categories: algebraic branch points, transcendental branch points, and logarithmic branch points. Algebraic branch points most commonly arise from functions in which there is an ambiguity in the extraction of a root, such as solving the equation ''w''2 = ''z'' for ''w'' as a function of ''z''. Here the branch point is the origin, because the analytic continuation of any solution around a closed loop containing the origin will result in a different function: there is non-trivial monodromy. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivalued Function
In mathematics, a multivalued function, also called multifunction, many-valued function, set-valued function, is similar to a function, but may associate several values to each input. More precisely, a multivalued function from a domain to a codomain associates each in to one or more values in ; it is thus a serial binary relation. Some authors allow a multivalued function to have no value for some inputs (in this case a multivalued function is simply a binary relation). However, in some contexts such as in complex analysis (''X'' = ''Y'' = C), authors prefer to mimic function theory as they extend concepts of the ordinary (single-valued) functions. In this context, an ordinary function is often called a single-valued function to avoid confusion. The term ''multivalued function'' originated in complex analysis, from analytic continuation. It often occurs that one knows the value of a complex analytic function f(z) in some neighbourhood of a point z=a. This is the cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modell Der Elliptischen Funktion φ=am (u, K) Durch Eine Fläche -Schilling V, 1 - 317-
Modell is the German word for "model" and also a surname. It may refer to: People * Arnold Modell (1924–2022), American professor of social psychiatry * Art Modell (1925–2012), American business executive and sports team owner * Bernadette Modell, (born 1935), British geneticist * David Modell (1961–2017), American business executive and sports team owner * Frank Modell (1917-2016), American cartoonist * Merriam Modell (1908–1994), American author of pulp fiction * Pat Modell (1931–2011), American TV actress * Rod Modell, given name for Deepchord, electronic music producer from Detroit, Michigan * William Modell (1921–2008), American businessman and chairman of Modell's Sporting Goods Companies * Modell's, a sporting goods retailer based in New York City * Modell (pawn shop), a pawnbroker based in New York City, originally formed as a spinoff of the sporting goods company * Schabak Modell, a die-cast toy producer in Germany * Schuco Modell, a die-cast t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
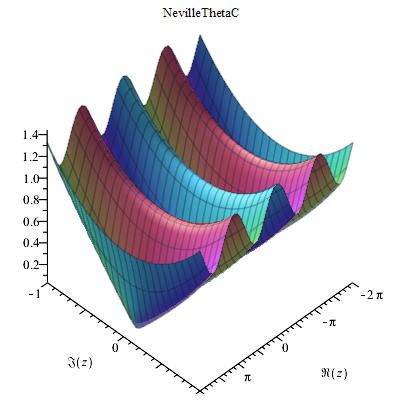
Neville Theta Function
In mathematics, the Neville theta functions, named after Eric Harold Neville, are defined as follows: : \theta_c(z,m)=\frac \,\, \sum _^\infty (q(m))^ \cos \left(\frac \right) : \theta_d(z,m)=\frac\,\,\left( 1+2\,\sum _^\infty (q(m))^ \cos \left( \frac \right) \right) : \theta_n(z, m) =\frac \,\,\left( 1+2\sum _^\infty (-1)^k (q(m))^ \cos \left(\frac \right) \right) : \theta_s(z, m)=\frac\,\, \sum_^\infty (-1)^k (q(m))^ \sin\left(\frac \right) where: ''K(m)'' is the complete elliptic integral of the first kind, K'(m)=K(1-m), and q(m)=e^ is the elliptic nome. Note that the functions ''θp(z,m)'' are sometimes defined in terms of the nome ''q(m)'' and written ''θp(z,q)'' (e.g. NIST). The functions may also be written in terms of the ''τ'' parameter ''θp(z, τ)'' where q=e^. Relationship to other functions The Neville theta functions may be expressed in terms of the Jacobi theta functions :\theta_s(z, \tau)=\theta_3^2(0, \tau)\theta_1(z' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Whitbread Lee Glaisher
James Whitbread Lee Glaisher FRS FRSE FRAS (5 November 1848, Lewisham – 7 December 1928, Cambridge), son of James Glaisher and Cecilia Glaisher, was a prolific English mathematician and astronomer. His large collection of (mostly) English ceramics was mostly left to the Fitzwilliam Museum in Cambridge. Life He was born in Lewisham in Kent on 5 November 1848 the son of the eminent astronomer James Glaisher and his wife, Cecilia Louisa Belville. His mother was a noted photographer. He was educated at St Paul's School from 1858. He became somewhat of a school celebrity in 1861 when he made two hot-air balloon ascents with his father to study the stratosphere. He won a Campden Exhibition Scholarship allowing him to study at Trinity College, Cambridge, where he was second wrangler in 1871 and was made a Fellow of the college. Influential in his time on teaching at the University of Cambridge, he is now remembered mostly for work in number theory that anticipated lat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Christof Gudermann
Christoph Gudermann (25 March 1798 – 25 September 1852) was a German mathematician noted for introducing the Gudermannian function and the concept of uniform convergence, and for being the teacher of Karl Weierstrass, who was greatly influenced by Gudermann's course on elliptic functions in 1839–1840, the first such course to be taught in any institute. Biography Gudermann was born in Vienenburg. He was the son of a school teacher and became a teacher himself after studying at the University of Göttingen, where his academic advisor was Karl Friedrich Gauss. He began his teaching career in Kleve and then transferred to a school in Münster. Gudermann introduced the concept of uniform convergence in an 1838 paper on elliptic functions, but only observed it informally, neither formalizing it nor using it in his proofs. Instead, Weierstrass elaborated and applied uniform convergence. His researches into spherical geometry and special function Special functions are pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |