|
Herbert Seifert
Herbert Karl Johannes Seifert (; 27 May 1897, Bernstadt – 1 October 1996, Heidelberg) was a German mathematician known for his work in topology. Biography Seifert was born in Bernstadt auf dem Eigen, but soon moved to Bautzen, where he attended primary school at the Knabenbürgerschule, and secondary school at the Oberrealschule. In 1926 Seifert entered the Dresden University of Technology. The next year he attended a course on topology given by William Threlfall. This would be the beginning both of his lifelong work in the subject and his friendship with Threlfall. In the year 1928–29 he visited the University of Göttingen, where topologists such as Pavel Sergeevich Alexandrov and Heinz Hopf were working. In 1930 he received his doctorate with his work on three-dimensional closed manifolds (which contains the Seifert–van Kampen theorem). He then moved to the University of Leipzig, where he received his second doctorate in 1932. It was here that Seifert submitte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernstadt Auf Dem Eigen
Bernstadt auf dem Eigen ( hsb, Bjenadźicy) is a town in the Görlitz district, in Saxony, Germany. It is situated 16 km north of Zittau, and 16 km southwest of Görlitz. History Within the German Empire (1871-1918), Bernstadt was part of the Kingdom of Saxony. Within the East German Bezirk Dresden, it was part of Kreis Löbau. Notable residents * Adolf Klose (1844-1923), machine engineer, Saxon State Railroad * Herbert Seifert (1907-1996), mathematician * Klaus Riedel Klaus Riedel (2 August 1907 – 4 August 1944) was a German rocket pioneer. He was involved in many early liquid-fuelled rocket experiments, and eventually worked on the V-2 missile programme at Peenemünde Army Research Center. History Ried ... (1907-1944), rocket pioneer References Populated places in Görlitz (district) {{Görlitz-geo-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
In mathematics, topology (from the Greek language, Greek words , and ) is concerned with the properties of a mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Twist (mathematics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity (mathematics), continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopy, homotopies. A property that is invariant under such deformations is a topological property. Basic exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luftwaffe
The ''Luftwaffe'' () was the aerial-warfare branch of the German ''Wehrmacht'' before and during World War II. Germany's military air arms during World War I, the ''Luftstreitkräfte'' of the Imperial Army and the '' Marine-Fliegerabteilung'' of the Imperial Navy, had been disbanded in May 1920 in accordance with the terms of the 1919 Treaty of Versailles which banned Germany from having any air force. During the interwar period, German pilots were trained secretly in violation of the treaty at Lipetsk Air Base in the Soviet Union. With the rise of the Nazi Party and the repudiation of the Versailles Treaty, the ''Luftwaffe''s existence was publicly acknowledged on 26 February 1935, just over two weeks before open defiance of the Versailles Treaty through German rearmament and conscription would be announced on 16 March. The Condor Legion, a ''Luftwaffe'' detachment sent to aid Nationalist forces in the Spanish Civil War, provided the force with a valuable testing grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
World War II
World War II or the Second World War, often abbreviated as WWII or WW2, was a world war that lasted from 1939 to 1945. It involved the vast majority of the world's countries—including all of the great powers—forming two opposing military alliances: the Allies and the Axis powers. World War II was a total war that directly involved more than 100 million personnel from more than 30 countries. The major participants in the war threw their entire economic, industrial, and scientific capabilities behind the war effort, blurring the distinction between civilian and military resources. Aircraft played a major role in the conflict, enabling the strategic bombing of population centres and deploying the only two nuclear weapons ever used in war. World War II was by far the deadliest conflict in human history; it resulted in 70 to 85 million fatalities, mostly among civilians. Tens of millions died due to genocides (including the Holocaust), starvation, ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Heidelberg
} Heidelberg University, officially the Ruprecht Karl University of Heidelberg, (german: Ruprecht-Karls-Universität Heidelberg; la, Universitas Ruperto Carola Heidelbergensis) is a public research university in Heidelberg, Baden-Württemberg, Germany. Founded in 1386 on instruction of Pope Urban VI, Heidelberg is Germany's oldest university and one of the world's oldest surviving universities; it was the third university established in the Holy Roman Empire. Heidelberg is one of the most prestigious and highly ranked universities in Europe and the world. Heidelberg has been a coeducational institution since 1899. The university consists of twelve faculties and offers degree programmes at undergraduate, graduate and postdoctoral levels in some 100 disciplines. The language of instruction is usually German, while a considerable number of graduate degrees are offered in English as well as some in French. As of 2021, 57 Nobel Prize winners have been affiliated with the city o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lehrbuch Der Topologie
In mathematics, ''Lehrbuch der Topologie'' (German for "textbook of topology") is a book by Herbert Seifert and William Threlfall, first published in 1934 and published in an English translation in 1980. It was one of the earliest textbooks on algebraic topology, and was the standard reference on this topic for many years. Albert W. Tucker wrote a review. Notes References * * Reprinted by Chelsea Publishing Company 1947 and AMS 2004. *{{Citation , last1=Seifert , first1=Herbert , last2=Threlfall , first2=William , editor1-last=Goldman , editor1-first=Michael A. , editor2-last=Birman , editor2-first=Joan S. , title=Seifert and Threlfall: a textbook of topology , url=https://books.google.com/books?id=rsb8zjP0XHoC , publisher=Academic Press Inc. [Harcourt Brace Jovanovich Publishers] , location=London , series=Pure and Applied Mathematics , isbn=978-0-12-634850-7 , mr=575168 , year=1980 , volume=89 History of mathematics Mathematics textbooks Algebraic topology ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
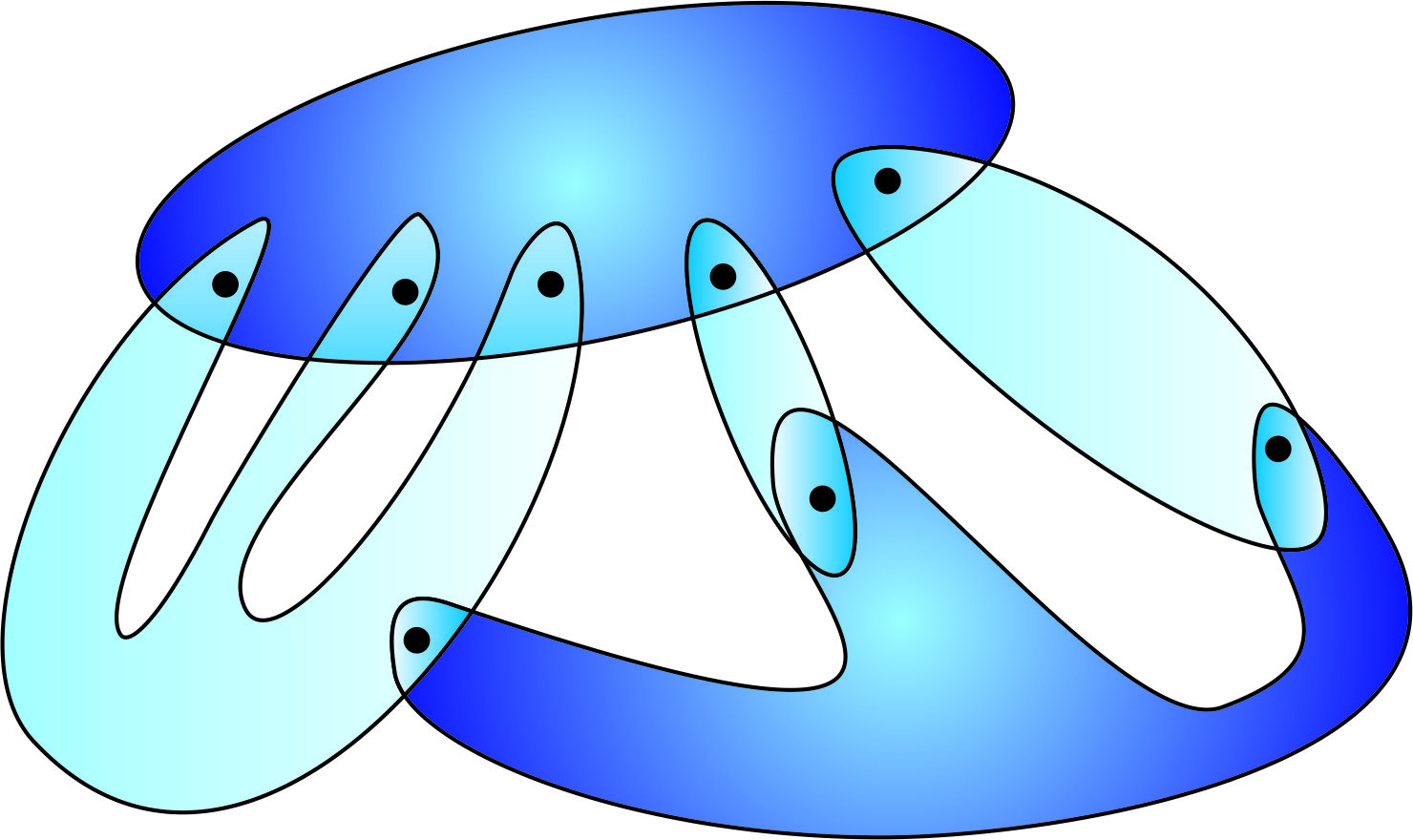
Seifert Fiber Space
A Seifert fiber space is a 3-manifold together with a decomposition as a disjoint union of circles. In other words, it is a S^1-bundle (circle bundle) over a 2-dimensional orbifold. Many 3-manifolds are Seifert fiber spaces, and they account for all compact oriented manifolds in 6 of the 8 Thurston geometries of the geometrization conjecture. Definition A Seifert manifold is a closed 3-manifold together with a decomposition into a disjoint union of circles (called fibers) such that each fiber has a tubular neighborhood that forms a standard fibered torus. A standard fibered torus corresponding to a pair of coprime integers (a,b) with a>0 is the surface bundle of the automorphism of a disk given by rotation by an angle of 2\pi b/a (with the natural fibering by circles). If a=1 the middle fiber is called ordinary, while if a>1 the middle fiber is called exceptional. A compact Seifert fiber space has only a finite number of exceptional fibers. The set of fibers forms a 2-dimensio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates (e.g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Leipzig
Leipzig University (german: Universität Leipzig), in Leipzig in Saxony, Germany, is one of the world's oldest universities and the second-oldest university (by consecutive years of existence) in Germany. The university was founded on 2 December 1409 by Frederick I, Elector of Saxony and his brother William II, Margrave of Meissen, and originally comprised the four scholastic faculties. Since its inception, the university has engaged in teaching and research for over 600 years without interruption. Famous alumni include Gottfried Wilhelm von Leibniz, Johann Wolfgang von Goethe, Leopold von Ranke, Friedrich Nietzsche, Robert Schumann, Richard Wagner, Tycho Brahe, Georgius Agricola, Angela Merkel and ten Nobel laureates associated with the university. History Founding and development until 1900 The university was modelled on the University of Prague, from which the German-speaking faculty members withdrew to Leipzig after the Jan Hus crisis and the Decree of Kutná H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seifert–van Kampen Theorem
In mathematics, the Seifert–Van Kampen theorem of algebraic topology (named after Herbert Seifert and Egbert van Kampen), sometimes just called Van Kampen's theorem, expresses the structure of the fundamental group of a topological space X in terms of the fundamental groups of two open, path-connected subspaces that cover X. It can therefore be used for computations of the fundamental group of spaces that are constructed out of simpler ones. Van Kampen's theorem for fundamental groups Let ''X'' be a topological space which is the union of two open and path connected subspaces ''U''1, ''U''2. Suppose ''U''1 ∩ ''U''2 is path connected and nonempty, and let ''x''0 be a point in ''U''1 ∩ ''U''2 that will be used as the base of all fundamental groups. The inclusion maps of ''U''1 and ''U''2 into ''X'' induce group homomorphisms j_1:\pi_1(U_1,x_0)\to \pi_1(X,x_0) and j_2:\pi_1(U_2,x_0)\to \pi_1(X,x_0). Then ''X'' is path connected and j_1 and j_2 form a commutative pushout dia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Manifold
In mathematics, a closed manifold is a manifold without boundary that is compact. In comparison, an open manifold is a manifold without boundary that has only ''non-compact'' components. Examples The only connected one-dimensional example is a circle. The sphere, torus, and the Klein bottle are all closed two-dimensional manifolds. A line is not closed because it is not compact. A closed disk is a compact two-dimensional manifold, but it is not closed because it has a boundary. Open manifolds For a connected manifold, "open" is equivalent to "without boundary and non-compact", but for a disconnected manifold, open is stronger. For instance, the disjoint union of a circle and a line is non-compact since a line is non-compact, but this is not an open manifold since the circle (one of its components) is compact. Abuse of language Most books generally define a manifold as a space that is, locally, homeomorphic to Euclidean space (along with some other technical con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pavel Sergeevich Alexandrov
Pavel Sergeyevich Alexandrov (russian: Па́вел Серге́евич Алекса́ндров), sometimes romanized ''Paul Alexandroff'' (7 May 1896 – 16 November 1982), was a Soviet mathematician. He wrote about three hundred papers, making important contributions to set theory and topology. In topology, the Alexandroff compactification and the Alexandrov topology are named after him. Biography Alexandrov attended Moscow State University where he was a student of Dmitri Egorov and Nikolai Luzin. Together with Pavel Urysohn, he visited the University of Göttingen in 1923 and 1924. After getting his Ph.D. in 1927, he continued to work at Moscow State University and also joined the Steklov Institute of Mathematics. He was made a member of the Russian Academy of Sciences in 1953. Personal life Luzin challenged Alexandrov to determine if the continuum hypothesis is true. This still unsolved problem was too much for Alexandrov and he had a creative crisis at the end of 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
