|
Heavy-tailed Distribution
In probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution. Roughly speaking, “heavy-tailed” means the distribution decreases more slowly than an exponential distribution, so extreme values are more likely. In many applications it is the right tail of the distribution that is of interest, but a distribution may have a heavy left tail, or both tails may be heavy. There are three important subclasses of heavy-tailed distributions: the fat-tailed distributions, the long-tailed distributions, and the subexponential distributions. In practice, all commonly used heavy-tailed distributions belong to the subexponential class, introduced by Jozef Teugels. There is still some discrepancy over the use of the term heavy-tailed. There are two other definitions in use. Some authors use the term to refer to those distributions which do not have all their p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Independence
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Distribution
The Cauchy distribution, named after Augustin-Louis Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution f(x; x_0,\gamma) is the distribution of the -intercept of a ray issuing from (x_0,\gamma) with a uniformly distributed angle. It is also the distribution of the Ratio distribution, ratio of two independent Normal distribution, normally distributed random variables with mean zero. The Cauchy distribution is often used in statistics as the canonical example of a "pathological (mathematics), pathological" distribution since both its expected value and its variance are undefined (but see below). The Cauchy distribution does not have finite moment (mathematics), moments of order greater than or equal to one; only fractional absolute moments exist., Chapter 16. The Cauchy dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Growth
In mathematics, logarithmic growth describes a phenomenon whose size or cost can be described as a logarithm function of some input. e.g. ''y'' = ''C'' log (''x''). Any logarithm base can be used, since one can be converted to another by multiplying by a fixed constant.. Logarithmic growth is the inverse of exponential growth and is very slow. A familiar example of logarithmic growth is a number, ''N'', in positional notation, which grows as log''b'' (''N''), where ''b'' is the base of the number system used, e.g. 10 for decimal arithmetic. In more advanced mathematics, the partial sums of the harmonic series :1+\frac+\frac+\frac+\frac+\cdots grow logarithmically. In the design of computer algorithms, logarithmic growth, and related variants, such as log-linear, or linearithmic, growth are very desirable indications of efficiency, and occur in the time complexity analysis of algorithms such as binary search. Logarithmic growth can lead to apparent paradoxes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-Cauchy Distribution
In probability theory, a log-Cauchy distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Cauchy distribution. If ''X'' is a random variable with a Cauchy distribution, then ''Y'' = exp(''X'') has a log-Cauchy distribution; likewise, if ''Y'' has a log-Cauchy distribution, then ''X'' = log(''Y'') has a Cauchy distribution. Characterization The log-Cauchy distribution is a special case of the log-t distribution where the degrees of freedom parameter is equal to 1. Probability density function The log-Cauchy distribution has the probability density function: :\begin f(x; \mu,\sigma) & = \frac, \ \ x>0 \\ & = \left \right \ \ x>0 \end where \mu is a real number and \sigma >0. If \sigma is known, the scale parameter is e^. \mu and \sigma correspond to the location parameter and scale parameter of the associated Cauchy distribution. Some authors define \mu and \sigma as the location and scale parameter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q-Gaussian Distribution
The ''q''-Gaussian is a probability distribution arising from the maximization of the Tsallis entropy under appropriate constraints. It is one example of a Tsallis distribution. The ''q''-Gaussian is a generalization of the Gaussian in the same way that Tsallis entropy is a generalization of standard Entropy (statistical thermodynamics), Boltzmann–Gibbs entropy or Entropy (information theory), Shannon entropy. The normal distribution is recovered as ''q'' → 1. The ''q''-Gaussian has been applied to problems in the fields of statistical mechanics, geology, anatomy, astronomy, economics, finance, and machine learning. The distribution is often favored for its heavy tails in comparison to the Gaussian for 1 < ''q'' < 3. For the ''q''-Gaussian distribution is the PDF of a bounded random variable. This makes in biology and other domains the ''q''-Gaussian distribution more suitable than Gaussian distribution to model the effect of external stochast ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fréchet Distribution
The Fréchet distribution, also known as inverse Weibull distribution, is a special case of the generalized extreme value distribution. It has the cumulative distribution function :\ \Pr(\ X \le x\ ) = e^ ~ \text ~ x > 0 ~. where is a shape parameter. It can be generalised to include a location parameter (the minimum) and a scale parameter with the cumulative distribution function :\ \Pr(\ X \le x\ ) = \exp\left[\ -\left( \tfrac \right)^\ \right] ~~ \text ~ x > m ~. Named for Maurice Fréchet who wrote a related paper in 1927, further work was done by Fisher–Tippett distribution, Fisher and Tippett in 1928 and by Emil Julius Gumbel, Gumbel in 1958. Characteristics The single parameter Fréchet, with parameter \ \alpha\ , has standardized moment :\mu_k = \int_0^\infty x^k f(x)\ \operatorname x =\int_0^\infty t^e^ \ \operatorname t\ , (with \ t = x^\ ) defined only for \ k1 the Expected value, expectation is E[X]=\Gamma(1-\tfrac) * For \alpha>2 the variance is \text(X)=\Gamma( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
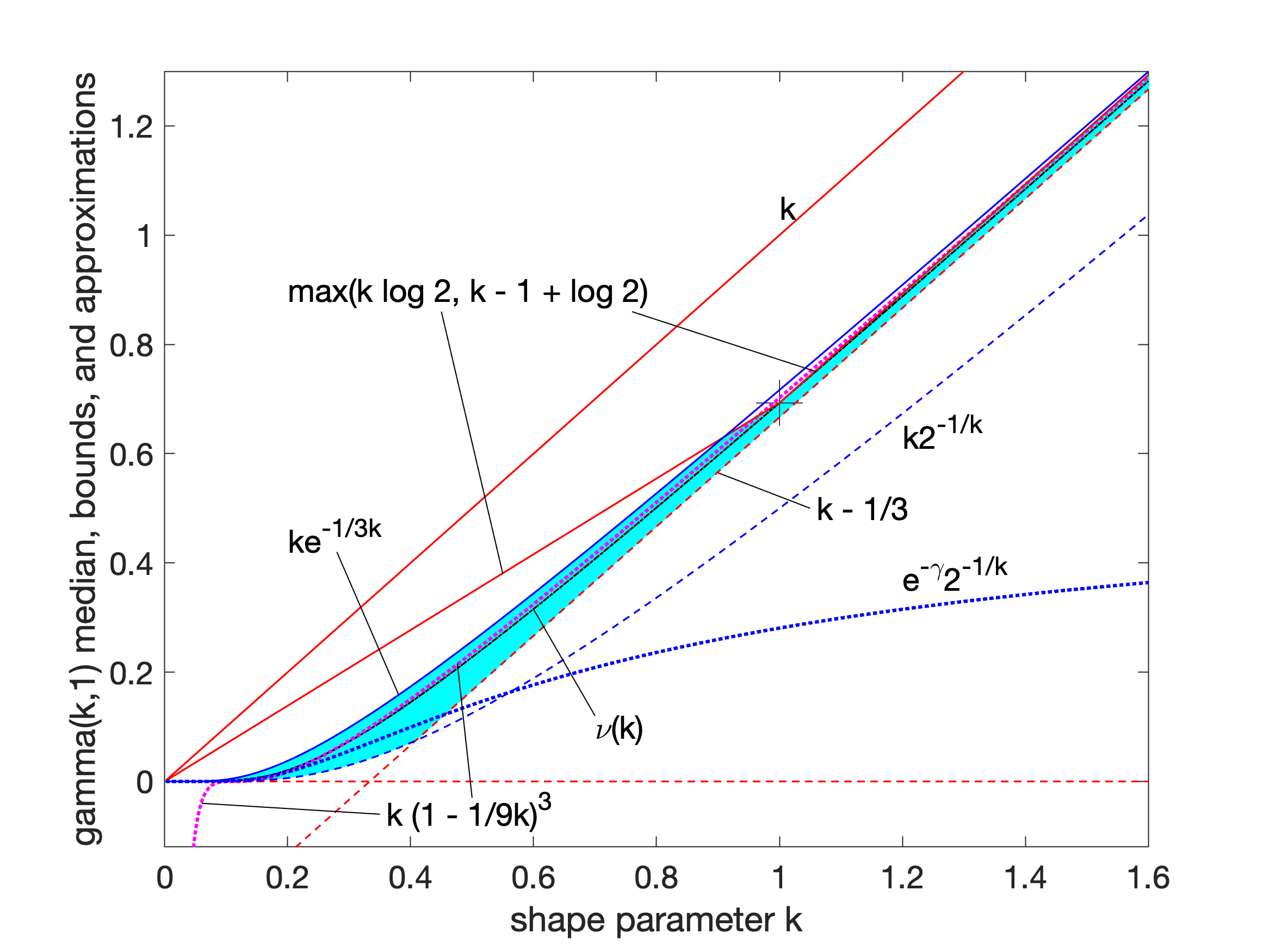
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-logistic Distribution
In probability and statistics, the log-logistic distribution (known as the Fisk distribution in economics) is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, as, for example, mortality rate from cancer following diagnosis or treatment. It has also been used in hydrology to model stream flow and precipitation, in economics as a simple model of the distribution of wealth or income, and in networking to model the transmission times of data considering both the network and the software. The log-logistic distribution is the probability distribution of a random variable whose logarithm has a logistic distribution. It is similar in shape to the log-normal distribution but has heavier tails. Unlike the log-normal, its cumulative distribution function can be written in closed form. Characterization There are several different parameterizations of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Burr Distribution
In probability theory, statistics and econometrics, the Burr Type XII distribution or simply the Burr distribution is a continuous probability distribution for a non-negative random variable. It is also known as the Singh–Maddala distribution and is one of a number of different distributions sometimes called the "generalized log-logistic distribution". Definitions Probability density function The Burr (Type XII) distribution has probability density function: : \begin f(x;c,k) & = ck\frac \\[6pt] f(x;c,k,\lambda) & = \frac \left( \frac \right)^ \left[1 + \left(\frac\right)^c\right]^ \end The \lambda parameter scales the underlying variate and is a positive real. Cumulative distribution function The cumulative distribution function is: :F(x;c,k) = 1-\left(1+x^c\right)^ :F(x;c,k,\lambda) = 1 - \left[1 + \left(\frac\right)^c \right]^ Applications It is most commonly used to model household income, see for example: Household income in the United States#Income distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weibull Distribution
In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page. The distribution is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1939, although it was first identified by René Maurice Fréchet and first applied by to describe a Particle-size distribution, particle size distribution. Definition Standard parameterization The probability density function of a Weibull random variable is : f(x;\lambda,k) = \begin \frac\left(\frac\right)^e^, & x\geq0 ,\\ 0, & x 0 is the ''shape parameter'' and λ > 0 is the ''scale parameter'' of the distribution. Its Cumulative distribution function#Complementary cumulative distribution function (tail distribution), complementary cumulative distribution function is a stretch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lévy Distribution
In probability theory and statistics, the Lévy distribution, named after Paul Lévy, is a continuous probability distribution for a non-negative random variable. In spectroscopy, this distribution, with frequency as the dependent variable, is known as a van der Waals profile."van der Waals profile" appears with lowercase "van" in almost all sources, such as: ''Statistical mechanics of the liquid surface'' by Clive Anthony Croxton, 1980, A Wiley-Interscience publication, , and in ''Journal of technical physics'', Volume 36, by Instytut Podstawowych Problemów Techniki (Polska Akademia Nauk), publisher: Państwowe Wydawn. Naukowe., 1995/ref> It is a special case of the inverse-gamma distribution. It is a stable distribution. Definition The probability density function of the Lévy distribution over the domain x \ge \mu is : f(x; \mu, c) = \sqrt \, \frac, where \mu is the location parameter, and c is the scale parameter. The cumulative distribution function is : F(x; \mu, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |