|
Greenberger–Horne–Zeilinger State
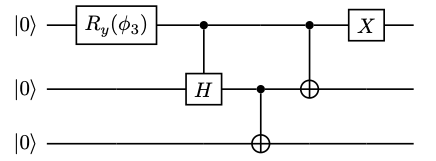
In physics, in the area of quantum information theory, a Greenberger–Horne–Zeilinger state (GHZ state) is a certain type of entangled quantum state that involves at least three subsystems (particle states, qubits, or qudits). It was first studied by Daniel Greenberger, Michael Horne and Anton Zeilinger in 1989. Extremely non-classical properties of the state have been observed. Definition The GHZ state is an entangled quantum state for 3 qubits and its state is :, \mathrm\rangle = \frac. Generalization The generalized GHZ state is an entangled quantum state of subsystems. If each system has dimension d, i.e., the local Hilbert space is isomorphic to \mathbb^d, then the total Hilbert space of partite system is \mathcal_=(\mathbb^d)^. This GHZ state is also named as M-partite qudit GHZ state, it reads :, \mathrm\rangle=\frac\sum_^, i\rangle\otimes\cdots\otimes, i\rangle=\frac(, 0\rangle\otimes\cdots\otimes, 0\rangle+\cdots+, d-1\rangle\otimes\cdots\otimes, d-1\rangle). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Quantum Logic Gates That Generates The 3-qubit GHZ State
''The'' () is a grammatical article in English, denoting persons or things that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of the archaic pron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
W State
The W state is an entangled quantum state of three qubits which in the bra-ket notation has the following shape : , \mathrm\rangle = \frac(, 001\rangle + , 010\rangle + , 100\rangle) and which is remarkable for representing a specific type of multipartite entanglement and for occurring in several applications in quantum information theory. Particles prepared in this state reproduce the properties of Bell's theorem, which states that no classical theory of local hidden variables can produce the predictions of quantum mechanics. The state is named after Wolfgang Dür, who first reported the state together with Guifré Vidal Guifré Vidal is a Spanish physicist who is working on quantum many-body physics using analytical and numerical techniques. In particular, he is one of the leading experts of tensor network state implementations such as time-evolving block deci ..., and Ignacio Cirac in 2002. Properties The W state is the representative of one of the two non-bisepara ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NOON State
In quantum optics, a NOON state or N00N state is a quantum-mechanical many-body Quantum entanglement, entangled state: : , \psi_\text \rangle = \frac, \, which represents a superposition of ''N'' particles in mode ''a'' with zero particles in mode ''b'', and vice versa. Usually, the particles are photons, but in principle any bosonic field can support NOON states. Applications NOON states are an important concept in quantum metrology and quantum sensing for their ability to make precision phase measurements when used in an optical Interferometry, interferometer. For example, consider the observable : A = , N,0\rangle\langle 0,N, + , 0,N\rangle\langle N,0, . \, The expectation value of A for a system in a NOON state switches between +1 and −1 when \theta changes from 0 to \pi/N. Moreover, the error in the phase measurement becomes : \Delta \theta = \frac = \frac. This is the so-called Heisenberg limit, and gives a quadratic improvement over the quantum limit, st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Hidden-variable Theory
In the interpretation of quantum mechanics, a local hidden-variable theory is a hidden-variable theory that satisfies the condition of being consistent with local realism. This includes all types of the theory that attempt to account for the probabilistic features of quantum mechanics by the mechanism of underlying inaccessible variables, with the additional requirement from local realism that distant events be independent, ruling out ''instantaneous'' (that is, faster-than-light) interactions between separate events. The mathematical implications of a local hidden-variable theory in regard to the phenomenon of quantum entanglement were explored by physicist John Stewart Bell, who in 1964 proved that broad classes of local hidden-variable theories cannot reproduce the correlations between measurement outcomes that quantum mechanics predicts. The most notable exception is superdeterminism. Superdeterministic hidden-variable theories can be local and yet be compatible with observati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Byzantine Agreement
Byzantine fault tolerant protocols are algorithms that are robust to arbitrary types of failures in distributed algorithms. The Byzantine agreement protocol is an essential part of this task. The constant-time quantum version of the Byzantine protocol, is described below. Introduction The Byzantine Agreement protocol is a protocol in distributed computing. It takes its name from a problem formulated by Lamport, Shostak and Pease in 1982, which itself is a reference to a historical problem. The Byzantine army was divided into divisions with each division being led by a General with the following properties: *Each General is either loyal or a traitor to the Byzantine state. *All Generals communicate by sending and receiving messages. *There are only two commands: attack and retreat. *All loyal Generals should agree on the same plan of action: attack or retreat. *A small linear fraction of bad Generals should not cause the protocol to fail (less than a \tfrac fraction). (See for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Gate
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate (or simply quantum gate) is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits. Unlike many classical logic gates, quantum logic gates are reversible. It is possible to perform classical computing using only reversible gates. For example, the reversible Toffoli gate can implement all Boolean functions, often at the cost of having to use ancilla bits. The Toffoli gate has a direct quantum equivalent, showing that quantum circuits can perform all operations performed by classical circuits. Quantum gates are unitary operators, and are described as unitary matrices relative to some basis. Usually we use the ''computational basis'', which unless we compare it with something, just means that for a ''d''-level quantum system (such as a qubit, a quantum register ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
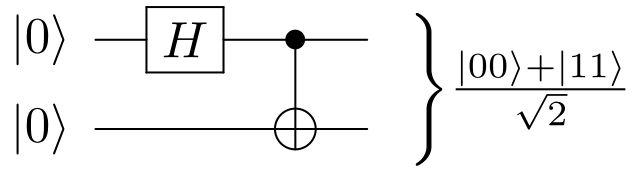
Bell State
The Bell states or EPR pairs are specific quantum states of two qubits that represent the simplest (and maximal) examples of quantum entanglement; conceptually, they fall under the study of quantum information science. The Bell states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particle being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will "collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell state the two qubits are in initially. Bell states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for 3 or more subsystems. Understand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Communication Complexity
In theoretical computer science, communication complexity studies the amount of communication required to solve a problem when the input to the problem is distributed among two or more parties. The study of communication complexity was first introduced by Andrew Yao in 1979, while studying the problem of computation distributed among several machines. The problem is usually stated as follows: two parties (traditionally called Alice and Bob) each receive a (potentially different) n-bit string x and y. The ''goal'' is for Alice to compute the value of a certain function, f(x, y), that depends on both x and y, with the least amount of communication between them. While Alice and Bob can always succeed by having Bob send his whole n-bit string to Alice (who then computes the function f), the idea here is to find clever ways of calculating ''f'' with fewer than n bits of communication. Note that, unlike in computational complexity theory, communication complexity is not concerned with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Cryptography
Quantum cryptography is the science of exploiting quantum mechanical properties to perform cryptographic tasks. The best known example of quantum cryptography is quantum key distribution which offers an information-theoretically secure solution to the key exchange problem. The advantage of quantum cryptography lies in the fact that it allows the completion of various cryptographic tasks that are proven or conjectured to be impossible using only classical (i.e. non-quantum) communication. For example, it is impossible to copy data encoded in a quantum state. If one attempts to read the encoded data, the quantum state will be changed due to wave function collapse (no-cloning theorem). This could be used to detect eavesdropping in quantum key distribution (QKD). History In the early 1970s, Stephen Wiesner, then at Columbia University in New York, introduced the concept of quantum conjugate coding. His seminal paper titled "Conjugate Coding" was rejected by the IEEE Information T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Information
Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information refers to both the technical definition in terms of Von Neumann entropy and the general computational term. It is an interdisciplinary field that involves quantum mechanics, computer science, information theory, philosophy and cryptography among other fields. Its study is also relevant to disciplines such as cognitive science, psychology and neuroscience. Its main focus is in extracting information from matter at the microscopic scale. Observation in science is one of the most important ways of acquiring information and measurement is required in order to quantify the observation, making this crucial to the scientific method. In quantum mechanics, due to the uncertainty principle, non-commuting observables cannot be precisely measured simultaneously, as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein–Podolsky–Rosen Paradox
The Einstein–Podolsky–Rosen (EPR) paradox is a thought experiment proposed by physicists Albert Einstein, Boris Podolsky and Nathan Rosen, with which they argued that the description of physical reality provided by quantum mechanics was incomplete. In a 1935 paper titled "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?", they argued for the existence of "elements of reality" that were not part of quantum theory, and speculated that it should be possible to construct a theory containing them. Resolutions of the paradox have important implications for the interpretation of quantum mechanics. The thought experiment involves a pair of particles prepared in what later authors would refer to as an entangled state. Einstein, Podolsky, and Rosen pointed out that, in this state, if the position of the first particle were measured, the result of measuring the position of the second particle could be predicted. If instead the momentum of the first particle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> The Quantum Logic Gates That Generates The 3-qubit GHZ State")
.jpg "Click for more on -> Quantum Information")
