W State

The W state is an entangled quantum state of three qubits which in the bra-ket notation has the following shape

: $, \mathrm\rangle = \frac(, 001\rangle + , 010\rangle + , 100\rangle)$
and which is remarkable for representing a specific type of multipartite entanglement and for occurring in several applications in quantum information theory. Particles prepared in this state reproduce the properties of Bell's theorem, which states that no classical theory of local hidden variables can produce the predictions of quantum mechanics. The state is named after Wolfgang Dür, who first reported the state together with Guifré Vidal, and Ignacio Cirac in 2002.

Properties

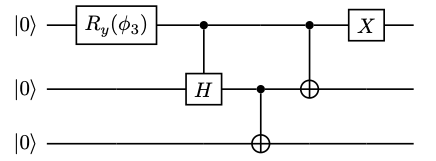The W state is the representative of one of the two non-biseparable classes of three-qubit states, the other being the Greenberger–Horne–Zeilinger state, $, \mathrm\rangle = (, 000\rangle + , 111\rangle)/\sqrt$, which cannot be transformed (not even probabilistically) into each other by local quantum operations. Thus $, \mathrm\rangle$ and $, \mathrm\rangle$ represent two very different kinds of tripartite entanglement.

This difference is, for example, illustrated by the following interesting property of the W state: if one of the three qubits is lost, the state of the remaining 2-qubit system is still entangled. This robustness of W-type entanglement contrasts strongly with the GHZ state, which is fully separable after loss of one qubit.

The states in the W class can be distinguished from all other 3-qubit states by means of multipartite entanglement measures. In particular, W states have non-zero entanglement across any bipartition, while the 3-tangle vanishes, which is also non-zero for GHZ-type states.

Generalization

The notion of W state has been generalized for $n$ qubits and then refers to the quantum superposition with equal expansion coefficients of all possible pure states in which exactly one of the qubits is in an "excited state" $, 1\rangle$, while all other ones are in the "ground state" $, 0\rangle$:
: $, \mathrm\rangle = \frac(, 100...0\rangle + , 010...0\rangle + ... + , 00...01\rangle).$
Both the robustness against particle loss and the LOCC-inequivalence with the (generalized) GHZ state also hold for the $n$-qubit W state.

Applications

In systems in which a single qubit is stored in an ensemble of many two-level systems the logical "1" is often represented by the W state, while the logical "0" is represented by the state $, 00...0\rangle$. Here the W state's robustness against particle loss is a very beneficial property ensuring good storage properties of these ensemble-based quantum memories.

See also

* NOON state

References

{{DEFAULTSORT:W State
Quantum information theory