|
Generalised Least Squares
In statistics, generalized least squares (GLS) is a technique for estimating the unknown parameters in a linear regression model when there is a certain degree of correlation between the residuals in a regression model. In these cases, ordinary least squares and weighted least squares can be statistically inefficient, or even give misleading inferences. GLS was first described by Alexander Aitken in 1936. Method outline In standard linear regression models we observe data \_ on ''n'' statistical units. The response values are placed in a vector \mathbf = \left( y_, \dots, y_ \right)^, and the predictor values are placed in the design matrix \mathbf = \left( \mathbf_^, \dots, \mathbf_^ \right)^, where \mathbf_ = \left( 1, x_, \dots, x_ \right) is a vector of the ''k'' predictor variables (including a constant) for the ''i''th unit. The model forces the conditional mean of \mathbf given \mathbf to be a linear function of \mathbf, and assumes the conditional variance of the erro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mahalanobis Distance
The Mahalanobis distance is a measure of the distance between a point ''P'' and a distribution ''D'', introduced by P. C. Mahalanobis in 1936. Mahalanobis's definition was prompted by the problem of identifying the similarities of skulls based on measurements in 1927. It is a multi-dimensional generalization of the idea of measuring how many standard deviations away ''P'' is from the mean of ''D''. This distance is zero for ''P'' at the mean of ''D'' and grows as ''P'' moves away from the mean along each principal component axis. If each of these axes is re-scaled to have unit variance, then the Mahalanobis distance corresponds to standard Euclidean distance in the transformed space. The Mahalanobis distance is thus unitless, scale-invariant, and takes into account the correlations of the data set. Definition Given a probability distribution Q on \R^N, with mean \vec = (\mu_1, \mu_2, \mu_3, \dots , \mu_N)^\mathsf and positive-definite covariance matrix S, the Mahalanobis dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Unit root processes, trend-stationary processes, autoregressive processes, and moving average processes are specific forms of processes with autocorrelation. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
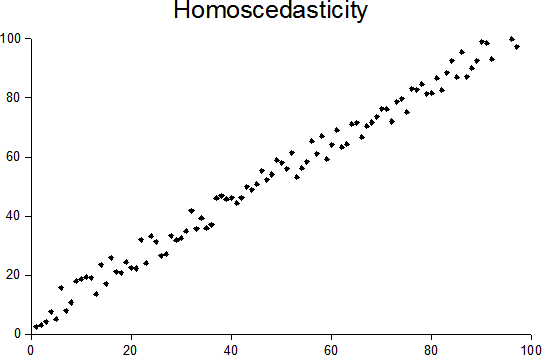
Heteroscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blue (statistics)
Blue is one of the three primary colours in the RYB colour model (traditional colour theory), as well as in the RGB (additive) colour model. It lies between violet and cyan on the spectrum of visible light. The eye perceives blue when observing light with a dominant wavelength between approximately 450 and 495 nanometres. Most blues contain a slight mixture of other colours; azure contains some green, while ultramarine contains some violet. The clear daytime sky and the deep sea appear blue because of an optical effect known as Rayleigh scattering. An optical effect called Tyndall effect explains blue eyes. Distant objects appear more blue because of another optical effect called aerial perspective. Blue has been an important colour in art and decoration since ancient times. The semi-precious stone lapis lazuli was used in ancient Egypt for jewellery and ornament and later, in the Renaissance, to make the pigment ultramarine, the most expensive of all pigments. In th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss–Markov Theorem
In statistics, the Gauss–Markov theorem (or simply Gauss theorem for some authors) states that the ordinary least squares (OLS) estimator has the lowest sampling variance within the class of linear unbiased estimators, if the errors in the linear regression model are uncorrelated, have equal variances and expectation value of zero. The errors do not need to be normal, nor do they need to be independent and identically distributed (only uncorrelated with mean zero and homoscedastic with finite variance). The requirement that the estimator be unbiased cannot be dropped, since biased estimators exist with lower variance. See, for example, the James–Stein estimator (which also drops linearity), ridge regression, or simply any degenerate estimator. The theorem was named after Carl Friedrich Gauss and Andrey Markov, although Gauss' work significantly predates Markov's. But while Gauss derived the result under the assumption of independence and normality, Markov reduced the assu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is consiste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. Terminology and notation The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. I_1 = \begin 1 \end ,\ I_2 = \begin 1 & 0 \\ 0 & 1 \end ,\ I_3 = \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end ,\ \dots ,\ I_n = \begin 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end. The term unit matrix has also been widely used, but the term ''identity matrix'' is now standard. The term ''unit matrix'' is ambiguous, because it is also used for a matrix of ones and for any unit of the ring of all n\times n matrices. In some fields, such as group theory or quantum mechanics, the identity matrix is sometimes denoted by a boldface one, \mathbf, or called "id" (short for identity). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cholesky Decomposition
In linear algebra, the Cholesky decomposition or Cholesky factorization (pronounced ) is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations. Statement The Cholesky decomposition of a Hermitian positive-definite matrix A, is a decomposition of the form : \mathbf = \mathbf^*, where L is a lower triangular matrix with real and positive diagonal entries, and L* denotes the conjugate transpose of L. Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition. The converse holds trivially: if A can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Distribution
In mathematics and statistics, an asymptotic distribution is a probability distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution functions of statistical estimators. Definition A sequence of distributions corresponds to a sequence of random variables ''Zi'' for ''i'' = 1, 2, ..., I . In the simplest case, an asymptotic distribution exists if the probability distribution of ''Zi'' converges to a probability distribution (the asymptotic distribution) as ''i'' increases: see convergence in distribution. A special case of an asymptotic distribution is when the sequence of random variables is always zero or ''Zi'' = 0 as ''i'' approaches infinity. Here the asymptotic distribution is a degenerate distribution, corresponding to the value zero. However, the most usual sense in which the term asymptotic distribution is used ari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consistent Estimator
In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter ''θ''0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to ''θ''0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to ''θ''0 converges to one. In practice one constructs an estimator as a function of an available sample of size ''n'', and then imagines being able to keep collecting data and expanding the sample ''ad infinitum''. In this way one would obtain a sequence of estimates indexed by ''n'', and consistency is a property of what occurs as the sample size “grows to infinity”. If the sequence of estimates can be mathematically shown to converge in probability to the true value ''� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bias Of An Estimator
In statistics, the bias of an estimator (or bias function) is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called ''unbiased''. In statistics, "bias" is an property of an estimator. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased; see bias versus consistency for more. All else being equal, an unbiased estimator is preferable to a biased estimator, although in practice, biased estimators (with generally small bias) are frequently used. When a biased estimator is used, bounds of the bias are calculated. A biased estimator may be used for various reasons: because an unbiased estimator does not exist without further assumptions about a population; because an estimator is difficult to compute (as in unbiased estimation of standard deviation); because a biased estimato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |