|
Fisher–Kolmogorov Equation
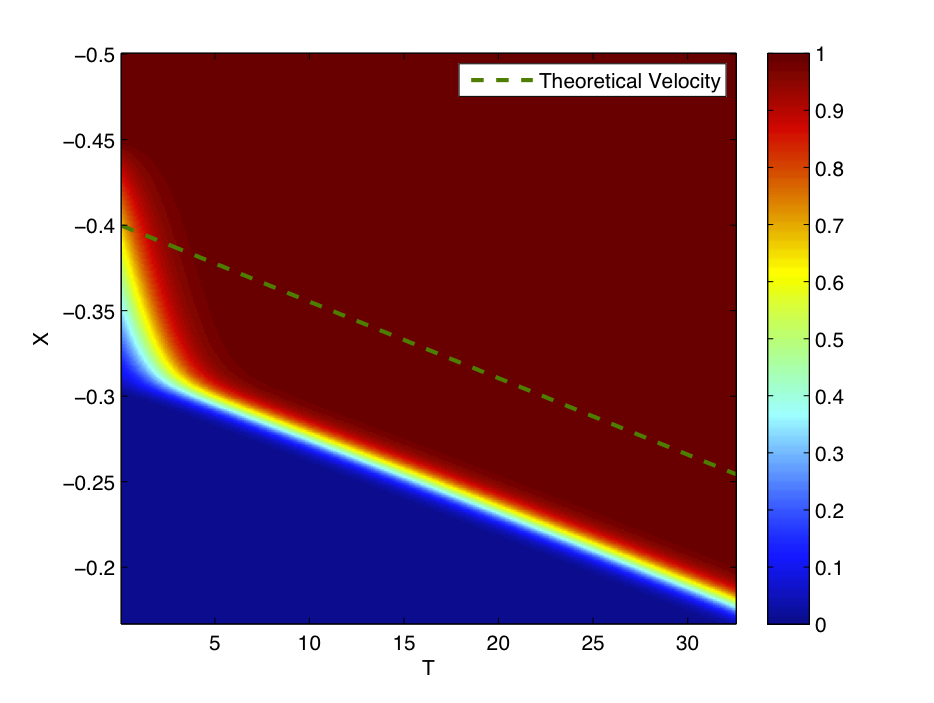
In mathematics, Fisher's equation (named after statistician and biologist Ronald Fisher) also known as the Kolmogorov–Petrovsky–Piskunov equation (named after Andrey Kolmogorov, Ivan Petrovsky, and Nikolai Piskunov), KPP equation or Fisher–KPP equation is the partial differential equation: : \frac - D \frac = r u(1-u).\, It is a kind of reaction–diffusion system that can be used to model population growth and wave propagation. Details Fisher's equation belongs to the class of reaction–diffusion equation: in fact, it is one of the simplest semilinear reaction-diffusion equations, the one which has the inhomogeneous term : f(u,x,t) = r u (1-u),\, which can exhibit traveling wave solutions that switch between equilibrium states given by f(u) = 0. Such equations occur, e.g., in ecology, physiology, combustion, crystallization, plasma physics, and in general phase transition problems. Fisher proposed this equation in his 1937 paper ''The wave of advance of advan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Equation
In financial mathematics and economics, the Fisher equation expresses the relationship between nominal interest rates and real interest rates under inflation. Named after Irving Fisher, an American economist, it can be expressed as real interest rate ≈ nominal interest rate − inflation rate. In more formal terms, where r equals the real interest rate, i equals the nominal interest rate, and \pi equals the inflation rate, the Fisher equation is r = i - \pi. It can also be expressed as i = r + \pi or (1 + i) = (1 + r) (1 + \pi). Applications Borrowing, lending and the time value of money When loans are made, the amount borrowed and the repayments due to the lender are normally stated in nominal terms, before inflation. However, when inflation occurs, a dollar repaid in the future is worth less than a dollar borrowed today. To calculate the true economics of the loan, it is necessary to adjust the nominal cash flows to account for future inflation. Inflation-indexed bonds The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallization
Crystallization is the process by which solid forms, where the atoms or molecules are highly organized into a structure known as a crystal. Some ways by which crystals form are precipitating from a solution, freezing, or more rarely deposition directly from a gas. Attributes of the resulting crystal depend largely on factors such as temperature, air pressure, and in the case of liquid crystals, time of fluid evaporation. Crystallization occurs in two major steps. The first is nucleation, the appearance of a crystalline phase from either a supercooled liquid or a supersaturated solvent. The second step is known as crystal growth, which is the increase in the size of particles and leads to a crystal state. An important feature of this step is that loose particles form layers at the crystal's surface and lodge themselves into open inconsistencies such as pores, cracks, etc. The majority of minerals and organic molecules crystallize easily, and the resulting crystals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign. History Eric W. Weisstein, the creator of the site, was a physics and astronomy student who got into the habit of writing notes on his mathematical readings. In 1995 he put his notes online and called it "Eric's Treasure Trove of Mathematics." It contained hundreds of pages/articles, covering a wide range of mathematical topics. The site became popular as an extensive single resource on mathematics on the web. Weisstein continuously improved the notes and accepted corrections and comments from online readers. In 1998, he made a contract with CRC Press and the contents of the site were published in print and CD-ROM form, titled "CRC Concise Encyclopedia of Mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allen–Cahn Equation
The Allen–Cahn equation (after John W. Cahn and Sam Allen) is a reaction–diffusion equation of mathematical physics which describes the process of phase separation in multi-component alloy systems, including order-disorder transitions. The equation describes the time evolution of a scalar-valued state variable \eta on a domain \Omega during a time interval \mathcal, and is given by: :=M_\eta operatorname(\varepsilon^_\nabla\,\eta)-f'(\eta)quad \text \Omega\times\mathcal, \quad \eta=\bar\eta\quad\text\partial_\eta\Omega\times\mathcal, :\quad -(\varepsilon^2_\eta\nabla\,\eta)\cdot m = q\quad\text \partial_q \Omega \times \mathcal, \quad \eta=\eta_o \quad\text \Omega\times\, where M_ is the mobility, f is a double-well potential, \bar\eta is the control on the state variable at the portion of the boundary \partial_\eta\Omega, q is the source control at \partial_q\Omega, \eta_o is the initial condition, and m is the outward normal to \partial\Omega. It is the L2 gradient fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Plasma (physics) Articles
This is a list of plasma physics topics. A * Ablation * Abradable coating * Abraham–Lorentz force * Absorption band * Accretion disk * Active galactic nucleus * Adiabatic invariant * ADITYA (tokamak) * Aeronomy * Afterglow plasma * Airglow * Air plasma, Corona treatment, Atmospheric-pressure plasma treatment * Ayaks, Novel "Magneto-plasmo-chemical engine" * Alcator C-Mod * Alfvén wave * Ambipolar diffusion * Aneutronic fusion * Anisothermal plasma * Anisotropy * Antiproton Decelerator * Appleton-Hartree equation * Arcing horns * Arc lamp * Arc suppression * ASDEX Upgrade, Axially Symmetric Divertor EXperiment * Astron (fusion reactor) * Astronomy * Astrophysical plasma * Astrophysical X-ray source * Atmospheric dynamo * Atmospheric escape * Atmospheric pressure discharge * Atmospheric-pressure plasma * Atom * Atomic emission spectroscopy * Atomic physics * Atomic-terrace low-angle shadowing * Auger electron spectroscopy * Aurora (astronomy) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ZFK Equation
ZFK equation, abbreviation for Zeldovich–Frank-Kamenetskii equation, is a reaction–diffusion equation that models premixed flame propagation. The equation is named after Yakov Zeldovich and David A. Frank-Kamenetskii who derived the equation in 1938 and is also known as the Nagumo equation. The equation is analogous to KPP equation except that is contains an exponential behaviour for the reaction term and it differs fundamentally from KPP equation with regards to the propagation velocity of the traveling wave. In non-dimensional form, the equation reads :\frac = \frac + \omega(\theta) with a typical form for \omega given by :\omega =\frac \theta(1-\theta) e^ where \theta\in ,1/math> is the non-dimensional dependent variable (typically temperature) and \beta is the Zeldovich number. In the ZFK regime, \beta\gg 1. The equation reduces to Fisher's equation for \beta\ll 1 and thus \beta\ll 1 corresponds to KPP regime. The minimum propagation velocity U_ (which is usually the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Genetics
Population genetics is a subfield of genetics that deals with genetic differences within and between populations, and is a part of evolutionary biology. Studies in this branch of biology examine such phenomena as adaptation, speciation, and population structure. Population genetics was a vital ingredient in the emergence of the modern evolutionary synthesis. Its primary founders were Sewall Wright, J. B. S. Haldane and Ronald Fisher, who also laid the foundations for the related discipline of quantitative genetics. Traditionally a highly mathematical discipline, modern population genetics encompasses theoretical, laboratory, and field work. Population genetic models are used both for statistical inference from DNA sequence data and for proof/disproof of concept. What sets population genetics apart from newer, more phenotypic approaches to modelling evolution, such as evolutionary game theory and adaptive dynamics, is its emphasis on such genetic phenomena as dominance, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Space Method
In applied mathematics, the phase space method is a technique for constructing and analyzing solutions of dynamical systems, that is, solving time-dependent differential equations. The method consists of first rewriting the equations as a system of differential equations that are first-order in time, by introducing additional variables. The original and the new variables form a vector in the phase space. The solution then becomes a curve in the phase space, parametrized by time. The curve is usually called a trajectory or an orbit. The (vector) differential equation is reformulated as a geometrical description of the curve, that is, as a differential equation in terms of the phase space variables only, without the original time parametrization. Finally, a solution in the phase space is transformed back into the original setting. The phase space method is used widely in physics. It can be applied, for example, to find traveling wave solutions of reaction–diffusion systems. A. Kolm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a ''traveling wave''; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a '' standing wave''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a '' wave equation'' (standing wave field of two opposite waves) or a one-way wave equation for single wave propagation in a defined direction. Two types of waves are most commonly studied in classical physics. In a '' mechanical wave'', stress and strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Eugenics
Annals ( la, annāles, from , "year") are a concise historical record in which events are arranged chronologically, year by year, although the term is also used loosely for any historical record. Scope The nature of the distinction between annals and history is a subject based on divisions established by the ancient Romans. Verrius Flaccus is quoted by Aulus Gellius as stating that the etymology of ''history'' (from Greek , , equated with Latin , "to inquire in person") properly restricts it to primary sources such as Thucydides's which have come from the author's own observations, while annals record the events of earlier times arranged according to years. White distinguishes annals from chronicles, which organize their events by topics such as the reigns of kings, and from histories, which aim to present and conclude a narrative implying the moral importance of the events recorded. Generally speaking, annalists record events drily, leaving the entries unexplained and equally we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allele
An allele (, ; ; modern formation from Greek ἄλλος ''állos'', "other") is a variation of the same sequence of nucleotides at the same place on a long DNA molecule, as described in leading textbooks on genetics and evolution. ::"The chromosomal or genomic location of a gene or any other genetic element is called a locus (plural: loci) and alternative DNA sequences at a locus are called alleles." The simplest alleles are single nucleotide polymorphisms (SNP). but they can also be insertions and deletions of up to several thousand base pairs. Popular definitions of 'allele' typically refer only to different alleles within genes. For example, the ABO blood grouping is controlled by the ABO gene, which has six common alleles (variants). In population genetics, nearly every living human's phenotype for the ABO gene is some combination of just these six alleles. Most alleles observed result in little or no change in the function of the gene product it codes for. However, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Dynamics
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems. History Population dynamics has traditionally been the dominant branch of mathematical biology, which has a history of more than 220 years,Malthus, Thomas Robert. An Essay on the Principle of Population: Library of Economics although over the last century the scope of mathematical biology has greatly expanded. The beginning of population dynamics is widely regarded as the work of Malthus, formulated as the Malthusian growth model. According to Malthus, assuming that the conditions (the environment) remain constant ('' ceteris paribus''), a population will grow (or decline) exponentially. This principle provided the basis for the subsequent predictive theories, such as the demographic studies such as the work of Benjamin Gompertz and Pierre François Verhulst in the early 19th century, who refined and adjusted the Malthusian demographic m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |