
In
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
,
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
,
engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
, and related fields, a wave is a propagating dynamic disturbance (change from
equilibrium) of one or more
quantities
Quantity or amount is a property that can exist as a multitude or magnitude, which illustrate discontinuity and continuity. Quantities can be compared in terms of "more", "less", or "equal", or by assigning a numerical value multiple of a u ...
. ''
Periodic waves'' oscillate repeatedly about an equilibrium (resting) value at some
frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
. When the entire
waveform
In electronics, acoustics, and related fields, the waveform of a signal is the shape of its Graph of a function, graph as a function of time, independent of its time and Magnitude (mathematics), magnitude Scale (ratio), scales and of any dis ...
moves in one direction, it is said to be a travelling wave; by contrast, a pair of
superimposed periodic waves traveling in opposite directions makes a ''
standing wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect t ...
''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero.
There are two types of waves that are most commonly studied in
classical physics
Classical physics refers to physics theories that are non-quantum or both non-quantum and non-relativistic, depending on the context. In historical discussions, ''classical physics'' refers to pre-1900 physics, while '' modern physics'' refers to ...
:
mechanical wave
In physics, a mechanical wave is a wave that is an oscillation of matter, and therefore transfers energy through a material medium.Giancoli, D. C. (2009) Physics for scientists & engineers with modern physics (4th ed.). Upper Saddle River, N.J. ...
s and
electromagnetic wave
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength, ...
s. In a mechanical wave,
stress and
strain fields oscillate about a
mechanical equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is ze ...
. A mechanical wave is a local
deformation (strain) in some physical medium that propagates from particle to particle by creating local
stresses that cause strain in neighboring particles too. For example,
sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
waves are variations of the local
pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
and
particle motion that propagate through the medium. Other examples of mechanical waves are
seismic wave
A seismic wave is a mechanical wave of acoustic energy that travels through the Earth or another planetary body. It can result from an earthquake (or generally, a quake), volcanic eruption, magma movement, a large landslide and a large ma ...
s,
gravity wave
In fluid dynamics, gravity waves are waves in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the oc ...
s,
surface wave
In physics, a surface wave is a mechanical wave that propagates along the Interface (chemistry), interface between differing media. A common example is gravity waves along the surface of liquids, such as ocean waves. Gravity waves can also occu ...
s and
string vibration
A vibration in a string is a wave. Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch. If the length or tension of the string is correctly adjusted, the sound produced is a musical tone. Vibratin ...
s. In an electromagnetic wave (such as light), coupling between the electric and magnetic fields sustains propagation of waves involving these fields according to
Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, Electrical network, electr ...
. Electromagnetic waves can travel through a
vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
and through some
dielectric
In electromagnetism, a dielectric (or dielectric medium) is an Insulator (electricity), electrical insulator that can be Polarisability, polarised by an applied electric field. When a dielectric material is placed in an electric field, electric ...
media (at wavelengths where they are considered
transparent). Electromagnetic waves, as determined by their frequencies (or
wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
s), have more specific designations including
radio wave
Radio waves (formerly called Hertzian waves) are a type of electromagnetic radiation with the lowest frequencies and the longest wavelengths in the electromagnetic spectrum, typically with frequencies below 300 gigahertz (GHz) and wavelengths g ...
s,
infrared radiation
Infrared (IR; sometimes called infrared light) is electromagnetic radiation (EMR) with wavelengths longer than that of visible light but shorter than microwaves. The infrared spectral band begins with the waves that are just longer than those ...
,
terahertz waves,
visible light
Light, visible light, or visible radiation is electromagnetic radiation that can be perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400–700 nanometres (nm ...
,
ultraviolet radiation
Ultraviolet radiation, also known as simply UV, is electromagnetic radiation of wavelengths of 10–400 nanometers, shorter than that of visible light, but longer than X-rays. UV radiation is present in sunlight and constitutes about 10% of t ...
,
X-ray
An X-ray (also known in many languages as Röntgen radiation) is a form of high-energy electromagnetic radiation with a wavelength shorter than those of ultraviolet rays and longer than those of gamma rays. Roughly, X-rays have a wavelength ran ...
s and
gamma ray
A gamma ray, also known as gamma radiation (symbol ), is a penetrating form of electromagnetic radiation arising from high energy interactions like the radioactive decay of atomic nuclei or astronomical events like solar flares. It consists o ...
s.
Other types of waves include
gravitational wave
Gravitational waves are oscillations of the gravitational field that Wave propagation, travel through space at the speed of light; they are generated by the relative motion of gravity, gravitating masses. They were proposed by Oliver Heaviside i ...
s, which are disturbances in
spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
that propagate according to
general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
;
heat diffusion waves;
plasma waves that combine mechanical deformations and electromagnetic fields;
reaction–diffusion waves, such as in the
Belousov–Zhabotinsky reaction; and many more. Mechanical and electromagnetic waves transfer
energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
,
momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
, and
information
Information is an Abstraction, abstract concept that refers to something which has the power Communication, to inform. At the most fundamental level, it pertains to the Interpretation (philosophy), interpretation (perhaps Interpretation (log ...
, but they do not transfer particles in the medium. In mathematics and
electronics
Electronics is a scientific and engineering discipline that studies and applies the principles of physics to design, create, and operate devices that manipulate electrons and other Electric charge, electrically charged particles. It is a subfield ...
waves are studied as
signal
A signal is both the process and the result of transmission of data over some media accomplished by embedding some variation. Signals are important in multiple subject fields including signal processing, information theory and biology.
In ...
s. On the other hand, some waves have
envelopes
An envelope is a common packaging item, usually made of thin, flat material. It is designed to contain a flat object, such as a letter or card.
Traditional envelopes are made from sheets of paper cut to one of three shapes: a rhombus, a sho ...
which do not move at all such as
standing wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect t ...
s (which are fundamental to music) and
hydraulic jumps.

A physical wave
field is almost always confined to some finite region of space, called its ''domain''. For example, the seismic waves generated by
earthquakes
An earthquakealso called a quake, tremor, or tembloris the shaking of the Earth's surface resulting from a sudden release of energy in the lithosphere that creates seismic waves. Earthquakes can range in intensity, from those so weak they c ...
are significant only in the interior and surface of the planet, so they can be ignored outside it. However, waves with infinite domain, that extend over the whole space, are commonly studied in mathematics, and are very valuable tools for understanding physical waves in finite domains.
A ''
plane wave
In physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of ...
'' is an important mathematical idealization where the disturbance is identical along any (infinite) plane
normal to a specific direction of travel. Mathematically, the simplest wave is a ''
sinusoidal plane wave'' in which at any point the field experiences
simple harmonic motion at one frequency. In linear media, complicated waves can generally be decomposed as the sum of many sinusoidal plane waves having
different directions of propagation and/or
different frequencies. A plane wave is classified as a ''
transverse wave
In physics, a transverse wave is a wave that oscillates perpendicularly to the direction of the wave's advance. In contrast, a longitudinal wave travels in the direction of its oscillations. All waves move energy from place to place without t ...
'' if the field disturbance at each point is described by a vector perpendicular to the direction of propagation (also the direction of energy transfer); or ''
longitudinal wave
Longitudinal waves are waves which oscillate in the direction which is parallel to the direction in which the wave travels and displacement of the medium is in the same (or opposite) direction of the wave propagation. Mechanical longitudinal ...
'' if those vectors are aligned with the propagation direction. Mechanical waves include both transverse and longitudinal waves; on the other hand electromagnetic plane waves are strictly transverse while sound waves in fluids (such as air) can only be longitudinal. That physical direction of an oscillating field relative to the propagation direction is also referred to as the wave's ''
polarization'', which can be an important attribute.
Mathematical description
Single waves
A wave can be described just like a field, namely as a
function where
is a position and
is a time.
The value of
is a point of space, specifically in the region where the wave is defined. In mathematical terms, it is usually a
vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
in the
Cartesian three-dimensional space . However, in many cases one can ignore one dimension, and let
be a point of the Cartesian plane
. This is the case, for example, when studying vibrations of a drum skin. One may even restrict
to a point of the Cartesian line
– that is, the set of
real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s. This is the case, for example, when studying vibrations in a
violin string or
recorder. The time
, on the other hand, is always assumed to be a
scalar; that is, a real number.
The value of
can be any physical quantity of interest assigned to the point
that may vary with time. For example, if
represents the vibrations inside an elastic solid, the value of
is usually a vector that gives the current displacement from
of the material particles that would be at the point
in the absence of vibration. For an electromagnetic wave, the value of
can be the
electric field
An electric field (sometimes called E-field) is a field (physics), physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) descri ...
vector
, or the
magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
vector
, or any related quantity, such as the
Poynting vector
In physics, the Poynting vector (or Umov–Poynting vector) represents the directional energy flux (the energy transfer per unit area, per unit time) or '' power flow'' of an electromagnetic field. The SI unit of the Poynting vector is the wat ...
. In
fluid dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion ...
, the value of
could be the velocity vector of the fluid at the point
, or any scalar property like
pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
,
temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
, or
density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
. In a chemical reaction,
could be the concentration of some substance in the neighborhood of point
of the reaction medium.
For any dimension
(1, 2, or 3), the wave's domain is then a
subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they a ...
of
, such that the function value
is defined for any point
in
. For example, when describing the motion of a
drum skin, one can consider
to be a
disk (circle) on the plane
with center at the origin
, and let
be the vertical displacement of the skin at the point
of
and at time
.
Superposition
Waves of the same type are often superposed and encountered simultaneously at a given point in space and time. The properties at that point are the sum of the properties of each component wave at that point. In general, the velocities are not the same, so the wave form will change over time and space.
Wave spectrum
Wave families
Sometimes one is interested in a single specific wave. More often, however, one needs to understand large set of possible waves; like all the ways that a drum skin can vibrate after being struck once with a
drum stick, or all the possible
radar
Radar is a system that uses radio waves to determine the distance ('' ranging''), direction ( azimuth and elevation angles), and radial velocity of objects relative to the site. It is a radiodetermination method used to detect and track ...
echoes one could get from an
airplane
An airplane (American English), or aeroplane (Commonwealth English), informally plane, is a fixed-wing aircraft that is propelled forward by thrust from a jet engine, Propeller (aircraft), propeller, or rocket engine. Airplanes come in a vari ...
that may be approaching an
airport
An airport is an aerodrome with extended facilities, mostly for commercial Aviation, air transport. They usually consist of a landing area, which comprises an aerially accessible open space including at least one operationally active surf ...
.
In some of those situations, one may describe such a family of waves by a function
that depends on certain
parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
s
, besides
and
. Then one can obtain different waves – that is, different functions of
and
– by choosing different values for those parameters.
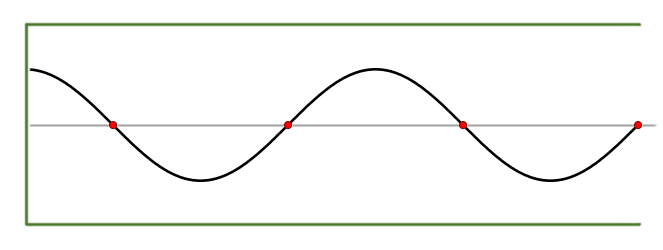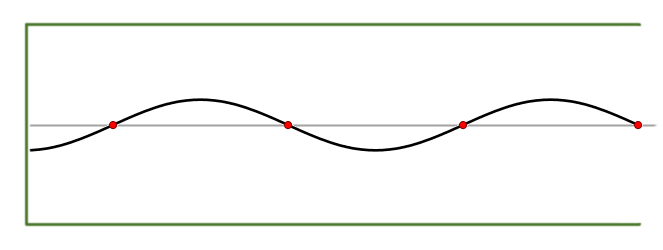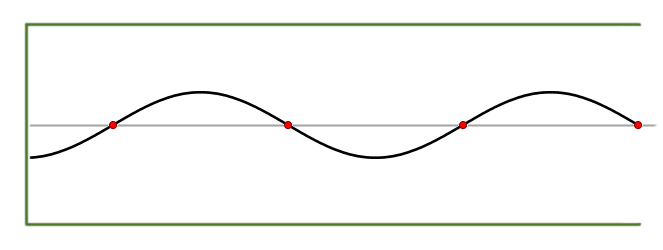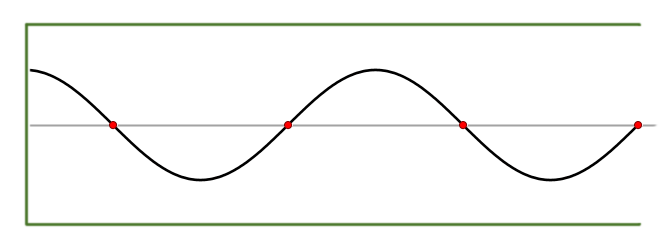
For example, the sound pressure inside a
recorder that is playing a "pure" note is typically a
standing wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect t ...
, that can be written as
:
The parameter
defines the amplitude of the wave (that is, the maximum sound pressure in the bore, which is related to the loudness of the note);
is the speed of sound;
is the length of the bore; and
is a positive integer (1,2,3,...) that specifies the number of
nodes in the standing wave. (The position
should be measured from the
mouthpiece, and the time
from any moment at which the pressure at the mouthpiece is maximum. The quantity
is the
wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
of the emitted note, and
is its
frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
.) Many general properties of these waves can be inferred from this general equation, without choosing specific values for the parameters.
As another example, it may be that the vibrations of a drum skin after a single strike depend only on the distance
from the center of the skin to the strike point, and on the strength
of the strike. Then the vibration for all possible strikes can be described by a function
.
Sometimes the family of waves of interest has infinitely many parameters. For example, one may want to describe what happens to the temperature in a metal bar when it is initially heated at various temperatures at different points along its length, and then allowed to cool by itself in vacuum. In that case, instead of a scalar or vector, the parameter would have to be a function
such that
is the initial temperature at each point
of the bar. Then the temperatures at later times can be expressed by a function
that depends on the function
(that is, a
functional operator), so that the temperature at a later time is
Differential wave equations
Another way to describe and study a family of waves is to give a mathematical equation that, instead of explicitly giving the value of
, only constrains how those values can change with time. Then the family of waves in question consists of all functions
that satisfy those constraints – that is, all
solutions
Solution may refer to:
* Solution (chemistry), a mixture where one substance is dissolved in another
* Solution (equation), in mathematics
** Numerical solution, in numerical analysis, approximate solutions within specified error bounds
* Solutio ...
of the equation.
This approach is extremely important in physics, because the constraints usually are a consequence of the physical processes that cause the wave to evolve. For example, if
is the temperature inside a block of some
homogeneous
Homogeneity and heterogeneity are concepts relating to the uniformity of a substance, process or image. A homogeneous feature is uniform in composition or character (i.e., color, shape, size, weight, height, distribution, texture, language, i ...
and
isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also ...
solid material, its evolution is constrained by the
partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
:
where
is the heat that is being generated per unit of volume and time in the neighborhood of
at time
(for example, by chemical reactions happening there);
are the Cartesian coordinates of the point
;
is the (first) derivative of
with respect to
; and
is the second derivative of
relative to
. (The symbol "
" is meant to signify that, in the derivative with respect to some variable, all other variables must be considered fixed.)
This equation can be derived from the laws of physics that govern the
diffusion of heat in solid media. For that reason, it is called the
heat equation
In mathematics and physics (more specifically thermodynamics), the heat equation is a parabolic partial differential equation. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quanti ...
in mathematics, even though it applies to many other physical quantities besides temperatures.
For another example, we can describe all possible sounds echoing within a container of gas by a function
that gives the pressure at a point
and time
within that container. If the gas was initially at uniform temperature and composition, the evolution of
is constrained by the formula
:
Here
is some extra compression force that is being applied to the gas near
by some external process, such as a
loudspeaker
A loudspeaker (commonly referred to as a speaker or, more fully, a speaker system) is a combination of one or more speaker drivers, an enclosure, and electrical connections (possibly including a crossover network). The speaker driver is an ...
or
piston
A piston is a component of reciprocating engines, reciprocating pumps, gas compressors, hydraulic cylinders and pneumatic cylinders, among other similar mechanisms. It is the moving component that is contained by a cylinder (engine), cylinder a ...
right next to
.
This same differential equation describes the behavior of mechanical vibrations and electromagnetic fields in a homogeneous isotropic non-conducting solid. Note that this equation differs from that of heat flow only in that the left-hand side is
, the second derivative of
with respect to time, rather than the first derivative
. Yet this small change makes a huge difference on the set of solutions
. This differential equation is called "the"
wave equation
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light ...
in mathematics, even though it describes only one very special kind of waves.
Wave in elastic medium
Consider a traveling
transverse wave
In physics, a transverse wave is a wave that oscillates perpendicularly to the direction of the wave's advance. In contrast, a longitudinal wave travels in the direction of its oscillations. All waves move energy from place to place without t ...
(which may be a
pulse
In medicine, the pulse refers to the rhythmic pulsations (expansion and contraction) of an artery in response to the cardiac cycle (heartbeat). The pulse may be felt ( palpated) in any place that allows an artery to be compressed near the surfac ...
) on a string (the medium). Consider the string to have a single spatial dimension. Consider this wave as traveling


* in the
direction in space. For example, let the positive
direction be to the right, and the negative
direction be to the left.
* with constant
amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of am ...
* with constant velocity
, where
is
** independent of
wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
(no
dispersion)
** independent of amplitude (
linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
media, not
nonlinear
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
).
* with constant
waveform
In electronics, acoustics, and related fields, the waveform of a signal is the shape of its Graph of a function, graph as a function of time, independent of its time and Magnitude (mathematics), magnitude Scale (ratio), scales and of any dis ...
, or shape
This wave can then be described by the two-dimensional functions
or, more generally, by
d'Alembert's formula
In mathematics, and specifically partial differential equations (PDEs), d´Alembert's formula is the general solution to the one-dimensional wave equation:
:u_-c^2u_=0,\, u(x,0)=g(x),\, u_t(x,0)=h(x),
for -\infty < x<\infty,\,\, t>0
It ...
:
representing two component waveforms
and
traveling through the medium in opposite directions. A generalized representation of this wave can be obtained as the
partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
General solutions are based upon
Duhamel's principle.
Wave forms

The form or shape of ''F'' in
d'Alembert's formula
In mathematics, and specifically partial differential equations (PDEs), d´Alembert's formula is the general solution to the one-dimensional wave equation:
:u_-c^2u_=0,\, u(x,0)=g(x),\, u_t(x,0)=h(x),
for -\infty < x<\infty,\,\, t>0
It ...
involves the argument ''x'' − ''vt''. Constant values of this argument correspond to constant values of ''F'', and these constant values occur if ''x'' increases at the same rate that ''vt'' increases. That is, the wave shaped like the function ''F'' will move in the positive ''x''-direction at velocity ''v'' (and ''G'' will propagate at the same speed in the negative ''x''-direction).
In the case of a periodic function ''F'' with period ''λ'', that is, ''F''(''x'' + ''λ'' − ''vt'') = ''F''(''x'' − ''vt''), the periodicity of ''F'' in space means that a snapshot of the wave at a given time ''t'' finds the wave varying periodically in space with period ''λ'' (the
wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
of the wave). In a similar fashion, this periodicity of ''F'' implies a periodicity in time as well: ''F''(''x'' − ''v''(''t'' + ''T'')) = ''F''(''x'' − ''vt'') provided ''vT'' = ''λ'', so an observation of the wave at a fixed location ''x'' finds the wave undulating periodically in time with period ''T'' = ''λ''/''v''.
Amplitude and modulation
The amplitude of a wave may be constant (in which case the wave is a ''c.w.'' or ''
continuous wave
A continuous wave or continuous waveform (CW) is an electromagnetic wave of constant amplitude and frequency, typically a sine wave, that for mathematical analysis is considered to be of infinite duration. It may refer to e.g. a laser or particl ...
''), or may be ''modulated'' so as to vary with time and/or position. The outline of the variation in amplitude is called the ''envelope'' of the wave. Mathematically, the
modulated wave can be written in the form:
where
is the amplitude envelope of the wave,
is the ''
wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
'' and
is the ''
phase''. If the
group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope (waves), envelope'' of the wave—propagates through space.
For example, if a stone is thro ...
(see below) is wavelength-independent, this equation can be simplified as:
showing that the envelope moves with the group velocity and retains its shape. Otherwise, in cases where the group velocity varies with wavelength, the pulse shape changes in a manner often described using an ''envelope equation''.
Phase velocity and group velocity
There are two velocities that are associated with waves, the phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, t ...
and the group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope (waves), envelope'' of the wave—propagates through space.
For example, if a stone is thro ...
.
Phase velocity is the rate at which the phase of the wave propagates in space: any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
(lambda) and period as
Group velocity is a property of waves that have a defined envelope, measuring propagation through space (that is, phase velocity) of the overall shape of the waves' amplitudes—modulation or envelope of the wave.
Special waves
Sine waves
Plane waves
A plane wave
In physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of ...
is a kind of wave whose value varies only in one spatial direction. That is, its value is constant on a plane that is perpendicular to that direction. Plane waves can be specified by a vector of unit length indicating the direction that the wave varies in, and a wave profile describing how the wave varies as a function of the displacement along that direction () and time (). Since the wave profile only depends on the position in the combination , any displacement in directions perpendicular to cannot affect the value of the field.
Plane waves are often used to model electromagnetic waves
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength, ran ...
far from a source. For electromagnetic plane waves, the electric and magnetic fields themselves are transverse to the direction of propagation, and also perpendicular to each other.
Standing waves
 A standing wave, also known as a ''stationary wave'', is a wave whose
A standing wave, also known as a ''stationary wave'', is a wave whose envelope
An envelope is a common packaging item, usually made of thin, flat material. It is designed to contain a flat object, such as a letter (message), letter or Greeting card, card.
Traditional envelopes are made from sheets of paper cut to one o ...
remains in a constant position. This phenomenon arises as a result of interference
Interference is the act of interfering, invading, or poaching. Interference may also refer to:
Communications
* Interference (communication), anything which alters, modifies, or disrupts a message
* Adjacent-channel interference, caused by extra ...
between two waves traveling in opposite directions.
The ''sum'' of two counter-propagating waves (of equal amplitude and frequency) creates a ''standing wave''. Standing waves commonly arise when a boundary blocks further propagation of the wave, thus causing wave reflection, and therefore introducing a counter-propagating wave. For example, when a violin
The violin, sometimes referred to as a fiddle, is a wooden chordophone, and is the smallest, and thus highest-pitched instrument (soprano) in regular use in the violin family. Smaller violin-type instruments exist, including the violino picc ...
string is displaced, transverse waves propagate out to where the string is held in place at the bridge
A bridge is a structure built to Span (engineering), span a physical obstacle (such as a body of water, valley, road, or railway) without blocking the path underneath. It is constructed for the purpose of providing passage over the obstacle, whi ...
and the nut, where the waves are reflected back. At the bridge and nut, the two opposed waves are in antiphase and cancel each other, producing a node
In general, a node is a localized swelling (a "knot") or a point of intersection (a vertex).
Node may refer to:
In mathematics
* Vertex (graph theory), a vertex in a mathematical graph
*Vertex (geometry), a point where two or more curves, lines ...
. Halfway between two nodes there is an antinode, where the two counter-propagating waves ''enhance'' each other maximally. There is no net propagation of energy over time.
Image:Standing waves on a string.gif, One-dimensional standing waves; the fundamental mode and the first 5 overtone
An overtone is any resonant frequency above the fundamental frequency of a sound. (An overtone may or may not be a harmonic) In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental i ...
s
Image:Drum vibration mode01.gif, A two-dimensional standing wave on a disk; this is the fundamental mode.
Image:Drum vibration mode21.gif, A standing wave on a disk with two nodal lines crossing at the center; this is an overtone.
Solitary waves
 A soliton or solitary wave is a self-reinforcing
A soliton or solitary wave is a self-reinforcing wave packet
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an Envelope (waves), envelope. A wave packet can be analyzed into, or can be synthesized from, a ...
that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
and dispersive effects in the medium. (Dispersive effects are a property of certain systems where the speed of a wave depends on its frequency.) Solitons are the solutions of a widespread class of weakly nonlinear dispersive partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s describing physical systems.
Physical properties
Propagation
Wave propagation is any of the ways in which waves travel. With respect to the direction of the oscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
relative to the propagation direction, we can distinguish between longitudinal wave
Longitudinal waves are waves which oscillate in the direction which is parallel to the direction in which the wave travels and displacement of the medium is in the same (or opposite) direction of the wave propagation. Mechanical longitudinal ...
and transverse wave
In physics, a transverse wave is a wave that oscillates perpendicularly to the direction of the wave's advance. In contrast, a longitudinal wave travels in the direction of its oscillations. All waves move energy from place to place without t ...
s.
Electromagnetic wave
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength, ...
s propagate in vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
as well as in material media. Propagation of other wave types such as sound may occur only in a transmission medium
A transmission medium is a system or substance that can mediate the propagation of signals for the purposes of telecommunication. Signals are typically imposed on a wave of some kind suitable for the chosen medium. For example, data can modula ...
.
Reflection of plane waves in a half-space
The propagation and reflection of plane waves—e.g. Pressure waves (P wave
A P wave (primary wave or pressure wave) is one of the two main types of elastic body waves, called seismic waves in seismology. P waves travel faster than other seismic waves and hence are the first signal from an earthquake to arrive at any ...
) or Shear waves (SH or SV-waves) are phenomena that were first characterized within the field of classical seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic ...
, and are now considered fundamental concepts in modern seismic tomography. The analytical solution to this problem exists and is well known. The frequency domain solution can be obtained by first finding the Helmholtz decomposition
In physics and mathematics, the Helmholtz decomposition theorem or the fundamental theorem of vector calculus states that certain differentiable vector fields can be resolved into the sum of an irrotational ( curl-free) vector field and a sole ...
of the displacement field, which is then substituted into the wave equation
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light ...
. From here, the plane wave eigenmodes can be calculated.
SV wave propagation

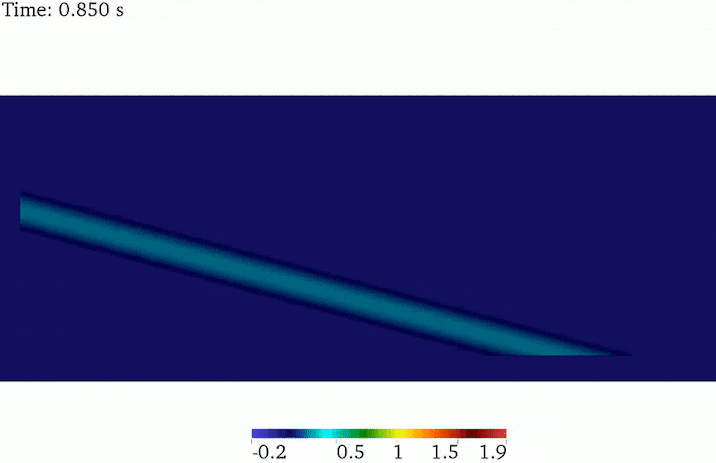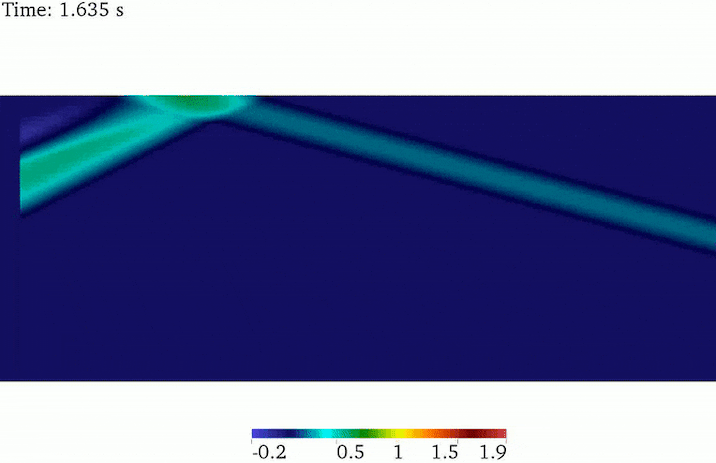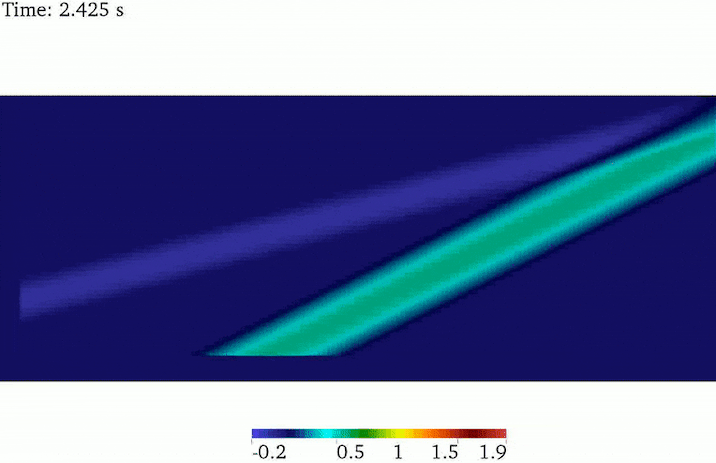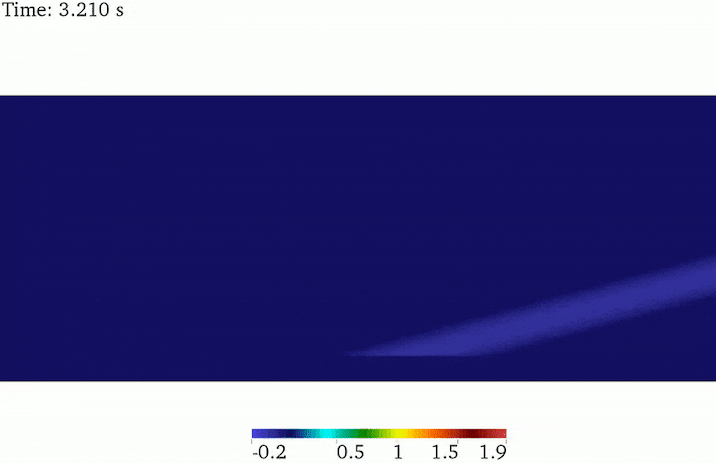 The analytical solution of SV-wave in a half-space indicates that the plane SV wave reflects back to the domain as a P and SV waves, leaving out special cases. The angle of the reflected SV wave is identical to the incidence wave, while the angle of the reflected P wave is greater than the SV wave. For the same wave frequency, the SV wavelength is smaller than the P wavelength. This fact has been depicted in this animated picture.
The analytical solution of SV-wave in a half-space indicates that the plane SV wave reflects back to the domain as a P and SV waves, leaving out special cases. The angle of the reflected SV wave is identical to the incidence wave, while the angle of the reflected P wave is greater than the SV wave. For the same wave frequency, the SV wavelength is smaller than the P wavelength. This fact has been depicted in this animated picture.
P wave propagation
Similar to the SV wave, the P incidence, in general, reflects as the P and SV wave. There are some special cases where the regime is different.
Wave velocity
Wave velocity is a general concept, of various kinds of wave velocities, for a wave's phase and speed
In kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a non-negative scalar quantity. Intro ...
concerning energy (and information) propagation. The phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, t ...
is given as:
where:
* ''v''p is the phase velocity (with SI unit m/s),
* ''ω'' is the angular frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine ...
(with SI unit rad/s),
* ''k'' is the wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
(with SI unit rad/m).
The phase speed gives you the speed at which a point of constant phase of the wave will travel for a discrete frequency. The angular frequency ''ω'' cannot be chosen independently from the wavenumber ''k'', but both are related through the dispersion relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the ...
ship:
In the special case , with ''c'' a constant, the waves are called non-dispersive, since all frequencies travel at the same phase speed ''c''. For instance electromagnetic wave
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength, ...
s in vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
are non-dispersive. In case of other forms of the dispersion relation, we have dispersive waves. The dispersion relationship depends on the medium through which the waves propagate and on the type of waves (for instance electromagnetic
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interacti ...
, sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
or water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
waves).
The speed at which a resultant wave packet
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an Envelope (waves), envelope. A wave packet can be analyzed into, or can be synthesized from, a ...
from a narrow range of frequencies will travel is called the group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope (waves), envelope'' of the wave—propagates through space.
For example, if a stone is thro ...
and is determined from the gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The g ...
of the dispersion relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the ...
:
In almost all cases, a wave is mainly a movement of energy through a medium. Most often, the group velocity is the velocity at which the energy moves through this medium.
Waves exhibit common behaviors under a number of standard situations, for example:
Transmission and media
Waves normally move in a straight line (that is, rectilinearly) through a ''transmission medium
A transmission medium is a system or substance that can mediate the propagation of signals for the purposes of telecommunication. Signals are typically imposed on a wave of some kind suitable for the chosen medium. For example, data can modula ...
''. Such media can be classified into one or more of the following categories:
* A ''bounded medium'' if it is finite in extent, otherwise an ''unbounded medium''
* A ''linear medium'' if the amplitudes of different waves at any particular point in the medium can be added
* A ''uniform medium'' or ''homogeneous medium'' if its physical properties are unchanged at different locations in space
* An ''anisotropic medium'' if one or more of its physical properties differ in one or more directions
* An ''isotropic medium'' if its physical properties are the ''same'' in all directions
Absorption
Waves are usually defined in media which allow most or all of a wave's energy to propagate without loss. However materials may be characterized as "lossy" if they remove energy from a wave, usually converting it into heat. This is termed "absorption." A material which absorbs a wave's energy, either in transmission or reflection, is characterized by a refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
which is complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
. The amount of absorption will generally depend on the frequency (wavelength) of the wave, which, for instance, explains why objects may appear colored.
Reflection
When a wave strikes a reflective surface, it changes direction, such that the angle made by the incident wave and line normal to the surface equals the angle made by the reflected wave and the same normal line.
Refraction
 Refraction is the phenomenon of a wave changing its speed. Mathematically, this means that the size of the
Refraction is the phenomenon of a wave changing its speed. Mathematically, this means that the size of the phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, t ...
changes. Typically, refraction occurs when a wave passes from one medium into another. The amount by which a wave is refracted by a material is given by the refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
of the material. The directions of incidence and refraction are related to the refractive indices of the two materials by Snell's law
Snell's law (also known as the Snell–Descartes law, the ibn-Sahl law, and the law of refraction) is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing th ...
.
Diffraction
A wave exhibits diffraction when it encounters an obstacle that bends the wave or when it spreads after emerging from an opening. Diffraction effects are more pronounced when the size of the obstacle or opening is comparable to the wavelength of the wave.
Interference
When waves in a linear medium (the usual case) cross each other in a region of space, they do not actually interact with each other, but continue on as if the other one were not present. However at any point ''in'' that region the ''field quantities'' describing those waves add according to the superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So th ...
. If the waves are of the same frequency in a fixed phase relationship, then there will generally be positions at which the two waves are ''in phase'' and their amplitudes ''add'', and other positions where they are ''out of phase'' and their amplitudes (partially or fully) ''cancel''. This is called an interference pattern.
Polarization
 The phenomenon of polarization arises when wave motion can occur simultaneously in two
The phenomenon of polarization arises when wave motion can occur simultaneously in two orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
directions. Transverse wave
In physics, a transverse wave is a wave that oscillates perpendicularly to the direction of the wave's advance. In contrast, a longitudinal wave travels in the direction of its oscillations. All waves move energy from place to place without t ...
s can be polarized, for instance. When polarization is used as a descriptor without qualification, it usually refers to the special, simple case of linear polarization. A transverse wave is linearly polarized if it oscillates in only one direction or plane. In the case of linear polarization, it is often useful to add the relative orientation of that plane, perpendicular to the direction of travel, in which the oscillation occurs, such as "horizontal" for instance, if the plane of polarization is parallel to the ground. Electromagnetic waves
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength, ran ...
propagating in free space, for instance, are transverse; they can be polarized by the use of a polarizing filter.
Longitudinal waves, such as sound waves, do not exhibit polarization. For these waves there is only one direction of oscillation, that is, along the direction of travel.
Dispersion
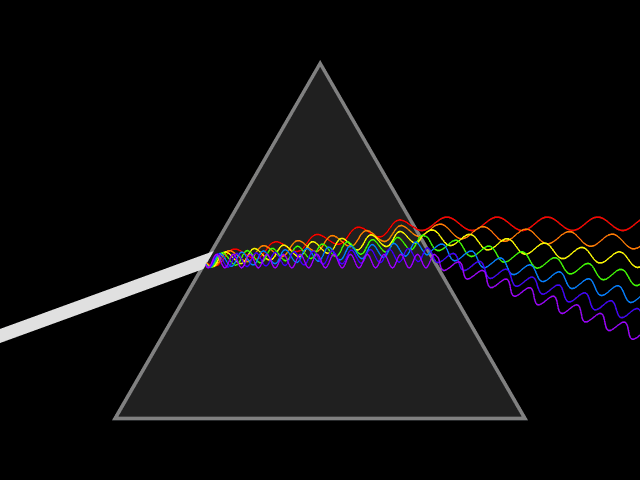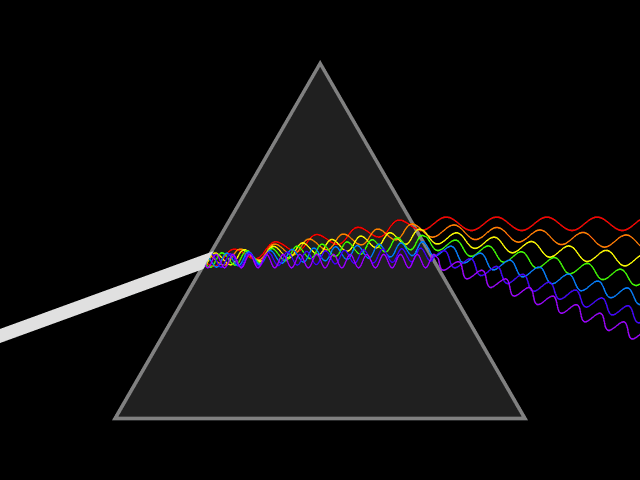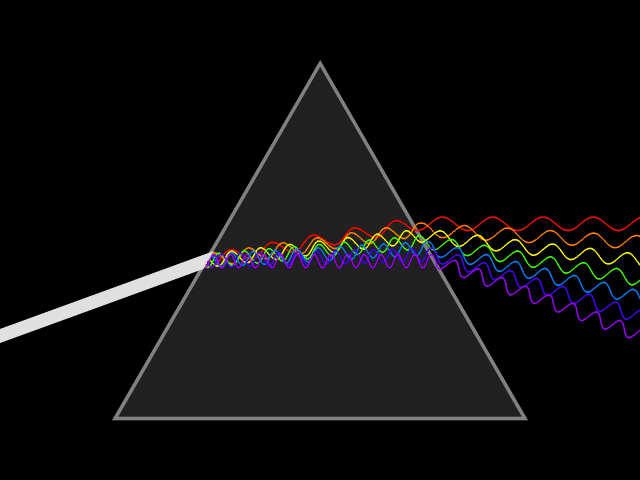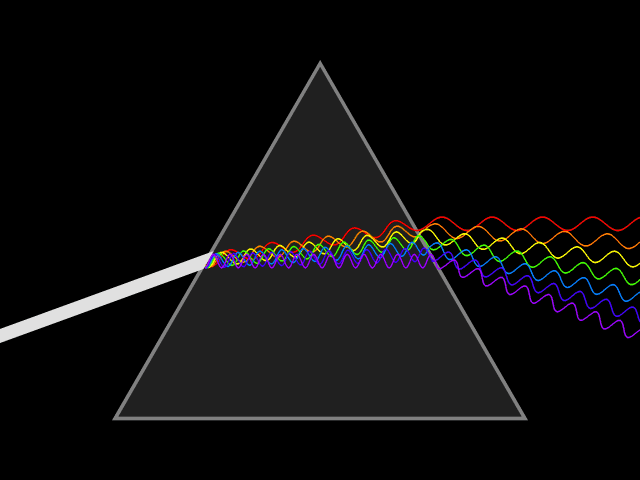 Dispersion is the frequency dependence of the
Dispersion is the frequency dependence of the refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
, a consequence of the atomic nature of materials.phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, t ...
or the group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope (waves), envelope'' of the wave—propagates through space.
For example, if a stone is thro ...
depends on the wave frequency. Dispersion is seen by letting white light pass through a prism, the result of which is to produce the spectrum of colors of the rainbow. Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
was the first to recognize that this meant that white light was a mixture of light of different colors.[
]
Doppler effect
The Doppler effect or Doppler shift is the change in frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
of a wave in relation to an observer who is moving relative to the wave source.Austria
Austria, formally the Republic of Austria, is a landlocked country in Central Europe, lying in the Eastern Alps. It is a federation of nine Federal states of Austria, states, of which the capital Vienna is the List of largest cities in Aust ...
n physicist Christian Doppler, who described the phenomenon in 1842.
Mechanical waves
A mechanical wave is an oscillation of matter
In classical physics and general chemistry, matter is any substance that has mass and takes up space by having volume. All everyday objects that can be touched are ultimately composed of atoms, which are made up of interacting subatomic pa ...
, and therefore transfers energy through a medium. While waves can move over long distances, the movement of the medium of transmission—the material—is limited. Therefore, the oscillating material does not move far from its initial position. Mechanical waves can be produced only in media which possess elasticity and inertia
Inertia is the natural tendency of objects in motion to stay in motion and objects at rest to stay at rest, unless a force causes the velocity to change. It is one of the fundamental principles in classical physics, and described by Isaac Newto ...
. There are three types of mechanical waves: transverse wave
In physics, a transverse wave is a wave that oscillates perpendicularly to the direction of the wave's advance. In contrast, a longitudinal wave travels in the direction of its oscillations. All waves move energy from place to place without t ...
s, longitudinal wave
Longitudinal waves are waves which oscillate in the direction which is parallel to the direction in which the wave travels and displacement of the medium is in the same (or opposite) direction of the wave propagation. Mechanical longitudinal ...
s, and surface wave
In physics, a surface wave is a mechanical wave that propagates along the Interface (chemistry), interface between differing media. A common example is gravity waves along the surface of liquids, such as ocean waves. Gravity waves can also occu ...
s.
Waves on strings
The transverse vibration of a string is a function of tension and inertia, and is constrained by the length of the string as the ends are fixed. This constraint limits the steady state modes that are possible, and thereby the frequencies.
The speed of a transverse wave traveling along a vibrating string (''v'') is directly proportional to the square root of the tension of the string (''T'') over the linear mass density (''μ''):
:
where the linear density ''μ'' is the mass per unit length of the string.
Acoustic waves
Acoustic or sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
waves are compression waves which travel as body waves at the speed given by:
:
or the square root of the adiabatic bulk modulus
The bulk modulus (K or B or k) of a substance is a measure of the resistance of a substance to bulk compression. It is defined as the ratio of the infinitesimal pressure increase to the resulting ''relative'' decrease of the volume.
Other mo ...
divided by the ambient density of the medium (see speed of sound
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elasticity (solid mechanics), elastic medium. More simply, the speed of sound is how fast vibrations travel. At , the speed of sound in a ...
).
Water waves
 * Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
*
* Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
* Sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
, a mechanical wave that propagates through gases, liquids, solids and plasmas.
* Inertial waves, which occur in rotating fluids and are restored by the Coriolis effect
In physics, the Coriolis force is a pseudo force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the moti ...
.
* Ocean surface wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of Body of water, bodies of water as a result of the wind blowing over the water's surface. The contact distance in the wind directi ...
s, which are perturbations that propagate through water.
Body waves
Body waves travel through the interior of the medium along paths controlled by the material properties in terms of density and modulus (stiffness). The density and modulus, in turn, vary according to temperature, composition, and material phase. This effect resembles the refraction of light waves. Two types of particle motion result in two types of body waves: Primary and Secondary waves.
Seismic waves
Seismic waves are waves of energy that travel through the Earth's layers, and are a result of earthquakes, volcanic eruptions, magma movement, large landslides and large man-made explosions that give out low-frequency acoustic energy. They include body waves—the primary (P wave
A P wave (primary wave or pressure wave) is one of the two main types of elastic body waves, called seismic waves in seismology. P waves travel faster than other seismic waves and hence are the first signal from an earthquake to arrive at any ...
s) and secondary waves (S wave
__NOTOC__
In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves (sometimes called elastic S waves) are a type of elastic wave and are one of the two main types of elastic body waves, so named because t ...
s)—and surface waves, such as Rayleigh waves
Rayleigh waves are a type of surface acoustic wave that travel along the surface of solids. They can be produced in materials in many ways, such as by a localized impact or by piezo-electric transduction, and are frequently used in non-destruc ...
, Love waves, and Stoneley waves.
Shock waves
 A shock wave is a type of propagating disturbance. When a wave moves faster than the local
A shock wave is a type of propagating disturbance. When a wave moves faster than the local speed of sound
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elasticity (solid mechanics), elastic medium. More simply, the speed of sound is how fast vibrations travel. At , the speed of sound in a ...
in a fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
, it is a shock wave. Like an ordinary wave, a shock wave carries energy and can propagate through a medium; however, it is characterized by an abrupt, nearly discontinuous change in pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
, temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
and density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
of the medium.
Shear waves
Shear waves are body waves due to shear rigidity and inertia. They can only be transmitted through solids and to a lesser extent through liquids with a sufficiently high viscosity.
Other
* Waves of traffic
Traffic is the movement of vehicles and pedestrians along land routes.
Traffic laws govern and regulate traffic, while rules of the road include traffic laws and informal rules that may have developed over time to facilitate the orderly an ...
, that is, propagation of different densities of motor vehicles, and so forth, which can be modeled as kinematic waves
Electromagnetic waves
An electromagnetic wave consists of two waves that are oscillations of the electric
Electricity is the set of physical phenomena associated with the presence and motion of matter possessing an electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by Maxwel ...
and magnetic
Magnetism is the class of physical attributes that occur through a magnetic field, which allows objects to attract or repel each other. Because both electric currents and magnetic moments of elementary particles give rise to a magnetic field, m ...
fields. An electromagnetic wave travels in a direction that is at right angles to the oscillation direction of both fields. In the 19th century, James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism an ...
showed that, in vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
, the electric and magnetic fields satisfy the wave equation
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light ...
both with speed equal to that of the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
. From this emerged the idea that light
Light, visible light, or visible radiation is electromagnetic radiation that can be visual perception, perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400– ...
is an electromagnetic wave. The unification of light and electromagnetic waves was experimentally confirmed by Hertz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), often described as being equivalent to one event (or Cycle per second, cycle) per second. The hertz is an SI derived unit whose formal expression in ter ...
in the end of the 1880s. Electromagnetic waves can have different frequencies (and thus wavelengths), and are classified accordingly in wavebands, such as radio waves
Radio waves (formerly called Hertzian waves) are a type of electromagnetic radiation with the lowest frequencies and the longest wavelengths in the electromagnetic spectrum, typically with frequencies below 300 gigahertz (GHz) and wavelengths ...
, microwaves
Microwave is a form of electromagnetic radiation with wavelengths shorter than other radio waves but longer than infrared waves. Its wavelength ranges from about one meter to one millimeter, corresponding to frequencies between 300 MHz an ...
, infrared
Infrared (IR; sometimes called infrared light) is electromagnetic radiation (EMR) with wavelengths longer than that of visible light but shorter than microwaves. The infrared spectral band begins with the waves that are just longer than those ...
, visible light
Light, visible light, or visible radiation is electromagnetic radiation that can be perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400–700 nanometres (nm ...
, ultraviolet
Ultraviolet radiation, also known as simply UV, is electromagnetic radiation of wavelengths of 10–400 nanometers, shorter than that of visible light, but longer than X-rays. UV radiation is present in sunlight and constitutes about 10% of ...
, X-rays
An X-ray (also known in many languages as Röntgen radiation) is a form of high-energy electromagnetic radiation with a wavelength shorter than those of ultraviolet rays and longer than those of gamma rays. Roughly, X-rays have a wavelength ran ...
, and gamma ray
A gamma ray, also known as gamma radiation (symbol ), is a penetrating form of electromagnetic radiation arising from high energy interactions like the radioactive decay of atomic nuclei or astronomical events like solar flares. It consists o ...
s. The range of frequencies in each of these bands is continuous, and the limits of each band are mostly arbitrary, with the exception of visible light, which must be visible to the normal human eye.
Quantum mechanical waves
Schrödinger equation
The Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
describes the wave-like behavior of particle
In the physical sciences, a particle (or corpuscle in older texts) is a small localized object which can be described by several physical or chemical properties, such as volume, density, or mass.
They vary greatly in size or quantity, from s ...
s in quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
. Solutions of this equation are wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s which can be used to describe the probability density of a particle.
Dirac equation
The Dirac equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac ...
is a relativistic wave equation detailing electromagnetic interactions. Dirac waves accounted for the fine details of the hydrogen spectrum in a completely rigorous way. The wave equation also implied the existence of a new form of matter, antimatter, previously unsuspected and unobserved and which was experimentally confirmed. In the context of quantum field theory, the Dirac equation is reinterpreted to describe quantum fields corresponding to spin- particles.
de Broglie waves
Louis de Broglie
Louis Victor Pierre Raymond, 7th Duc de Broglie (15 August 1892 – 19 March 1987) was a French theoretical physicist and aristocrat known for his contributions to quantum theory. In his 1924 PhD thesis, he postulated the wave nature of elec ...
postulated that all particles with momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
have a wavelength
:
where ''h'' is the Planck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
, and ''p'' is the magnitude of the momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
of the particle. This hypothesis was at the basis of quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
. Nowadays, this wavelength is called the de Broglie wavelength. For example, the electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
s in a CRT
CRT or Crt most commonly refers to:
* Cathode-ray tube, a display
* Critical race theory, an academic framework of analysis
CRT may also refer to:
Law
* Charitable remainder trust, United States
* Civil Resolution Tribunal, Canada
* Columbia ...
display have a de Broglie wavelength of about 10−13 m.
A wave representing such a particle traveling in the ''k''-direction is expressed by the wave function as follows:
:
where the wavelength is determined by the wave vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength) ...
k as:
:
and the momentum by:
:
However, a wave like this with definite wavelength is not localized in space, and so cannot represent a particle localized in space. To localize a particle, de Broglie proposed a superposition of different wavelengths ranging around a central value in a wave packet
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an Envelope (waves), envelope. A wave packet can be analyzed into, or can be synthesized from, a ...
,[
] a waveform often used in quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
to describe the wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
of a particle. In a wave packet, the wavelength of the particle is not precise, and the local wavelength deviates on either side of the main wavelength value.
In representing the wave function of a localized particle, the wave packet
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an Envelope (waves), envelope. A wave packet can be analyzed into, or can be synthesized from, a ...
is often taken to have a Gaussian shape and is called a ''Gaussian wave packet''.[
]
:
at some initial time ''t'' = 0, where the central wavelength is related to the central wave vector ''k''0 as ''λ''0 = 2π / ''k''0. It is well known from the theory of Fourier analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fo ...
,[
] or from the Heisenberg uncertainty principle
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position a ...
(in the case of quantum mechanics) that a narrow range of wavelengths is necessary to produce a localized wave packet, and the more localized the envelope, the larger the spread in required wavelengths. The Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
of a Gaussian is itself a Gaussian.[
] Given the Gaussian:
:
the Fourier transform is:
:
The Gaussian in space therefore is made up of waves:
:
that is, a number of waves of wavelengths ''λ'' such that ''kλ'' = 2 π.
The parameter σ decides the spatial spread of the Gaussian along the ''x''-axis, while the Fourier transform shows a spread in wave vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength) ...
''k'' determined by 1/''σ''. That is, the smaller the extent in space, the larger the extent in ''k'', and hence in ''λ'' = 2π/''k''.

Gravity waves
Gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy works to restore equilibrium. Surface waves on water are the most familiar example.
Gravitational waves
Gravitational waves
Gravitational waves are oscillations of the gravitational field that travel through space at the speed of light; they are generated by the relative motion of gravitating masses. They were proposed by Oliver Heaviside in 1893 and then later by H ...
also travel through space. The first observation of gravitational waves was announced on 11 February 2016.spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
, predicted by Einstein's theory of general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
.
See also
* Index of wave articles
Waves in general
Parameters
Waveforms
Electromagnetic waves
In fluids
* Airy wave theory, in fluid dynamics
* Capillary wave, in fluid dynamics
* Cnoidal wave, in fluid dynamics
* Edge wave, a surface gravity wave fixed by refraction against a rigid boundary
* Faraday wave, a type of wave in liquids
* Gravity wave
In fluid dynamics, gravity waves are waves in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the oc ...
, in fluid dynamics
* Internal wave, a wave within a fluid medium
* Shock wave
In physics, a shock wave (also spelled shockwave), or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a me ...
, in aerodynamics
* Sound wave, a wave of sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
through a medium such as air or water
* Tidal wave, a scientifically incorrect name for a tsunami
A tsunami ( ; from , ) is a series of waves in a water body caused by the displacement of a large volume of water, generally in an ocean or a large lake. Earthquakes, volcanic eruptions and underwater explosions (including detonations, ...
* Tollmien–Schlichting wave, in fluid dynamics
* Wind wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is ...
In quantum mechanics
In relativity
Other specific types of waves
* Alfvén wave
In plasma physics, an Alfvén wave, named after Hannes Alfvén, is a type of plasma wave in which ions oscillate in response to a restoring force provided by an Magnetic tension force, effective tension on the magnetic field lines.
Definition
...
, in plasma physics
* Atmospheric wave, a periodic disturbance in the fields of atmospheric variables
* Fir wave, a forest configuration
* Lamb waves, in solid materials
* Rayleigh wave
Rayleigh waves are a type of surface acoustic wave that travel along the surface of solids. They can be produced in materials in many ways, such as by a localized impact or by Piezoelectricity, piezo-electric Interdigital transducer, transduction, ...
, surface acoustic waves that travel on solids
* Spin wave, in magnetism
* Spin density wave, in solid materials
* Trojan wave packet, in particle science
* Waves in plasmas, in plasma physics
Related topics
* Absorption (electromagnetic radiation)
In physics, absorption of electromagnetic radiation is how matter (typically electrons bound in atoms) takes up a photon's energy—and so transforms electromagnetic energy into internal energy of the absorber (for example, thermal energy).
...
* Antenna (radio)
In radio-frequency engineering, an antenna (American English) or aerial (British English) is an electronic device that converts an alternating current, alternating electric current into radio waves (transmitting), or radio waves into an elect ...
* Beat (acoustics)
In acoustics, a beat is an interference pattern between two sounds of slightly different frequencies, ''perceived'' as a periodic variation in volume whose rate is the difference of the two frequencies.
With tuning instruments that can produc ...
* Branched flow
* Cymatics
* Diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
* Dispersion (water waves)
* Doppler effect
The Doppler effect (also Doppler shift) is the change in the frequency of a wave in relation to an observer who is moving relative to the source of the wave. The ''Doppler effect'' is named after the physicist Christian Doppler, who described ...
* Envelope detector
An envelope detector (sometimes called a peak detector) is an electronic circuit that takes a (relatively) high-frequency signal as input and outputs the '' envelope'' of the original signal.
Diode detector
A simple form of envelope detect ...
* Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
for computing periodicity in evenly spaced data
* Group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope (waves), envelope'' of the wave—propagates through space.
For example, if a stone is thro ...
* Harmonic
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st har ...
* Huygens–Fresnel principle
The Huygens–Fresnel principle (named after Netherlands, Dutch physicist Christiaan Huygens and France, French physicist Augustin-Jean Fresnel) states that every point on a wavefront is itself the source of spherical wavelets, and the secondary w ...
* Index of wave articles
* Inertial wave
* Least-squares spectral analysis
Least-squares spectral analysis (LSSA) is a method of estimating a Spectral density estimation#Overview, frequency spectrum based on a least-squares fit of Sine wave, sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the ...
for computing periodicity in unevenly spaced data
* List of waves named after people
* Phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, t ...
* Photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
* Polarization (physics)
, or , is a property of transverse waves which specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. One example of a polariz ...
* Propagation constant
The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a ...
* Radio propagation
Radio propagation is the behavior of radio waves as they travel, or are wave propagation, propagated, from one point to another in vacuum, or into various parts of the atmosphere.
As a form of electromagnetic radiation, like light waves, radio w ...
* Ray (optics)
In optics, a ray is an idealized geometrical model of light or other electromagnetic radiation, obtained by choosing a curve that is perpendicular to the ''wavefronts'' of the actual light, and that points in the direction of energy flow. Rays ...
* Reaction–diffusion system
* Reflection (physics)
Reflection is the change in direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves. The ...
* Refraction
In physics, refraction is the redirection of a wave as it passes from one transmission medium, medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commo ...
* Resonance
Resonance is a phenomenon that occurs when an object or system is subjected to an external force or vibration whose frequency matches a resonant frequency (or resonance frequency) of the system, defined as a frequency that generates a maximu ...
* Ripple tank
* Rogue wave A rogue wave is an abnormally large ocean wave.
Rogue wave may also refer to:
* Optical rogue waves, are rare pulses of light analogous to rogue or freak ocean waves.
* Rogue Wave Software, a software company
* Rogue Wave (band), an American in ...
* Scattering
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities (including particles and radiat ...
* Shallow water equations
* Shive wave machine
* Sound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
* Standing wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect t ...
* Transmission medium
A transmission medium is a system or substance that can mediate the propagation of signals for the purposes of telecommunication. Signals are typically imposed on a wave of some kind suitable for the chosen medium. For example, data can modula ...
* Velocity factor
* Wave equation
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light ...
* Wave power
Wave power is the capture of energy of wind waves to do useful mechanical work, work – for example, electricity generation, desalination, or pumping water. A machine that exploits wave power (physics), power is a wave energy converter (WEC).
W ...
* Wave turbulence
* Wind wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is ...
* Wind wave#Formation
References
Sources
*
*
*
* .
*
* .
*
* Crawford jr., Frank S. (1968). ''Waves (Berkeley Physics Course, Vol. 3)'', McGraw-Hill,
Free online version
*
*
External links
Linear and nonlinear waves
"AT&T Archives: Similiarities of Wave Behavior"
demonstrated by J.N. Shive of Bell Labs (video on YouTube
YouTube is an American social media and online video sharing platform owned by Google. YouTube was founded on February 14, 2005, by Steve Chen, Chad Hurley, and Jawed Karim who were three former employees of PayPal. Headquartered in ...
)
{{Authority control
Differential equations
Articles containing video clips
 In
In  A physical wave field is almost always confined to some finite region of space, called its ''domain''. For example, the seismic waves generated by
A physical wave field is almost always confined to some finite region of space, called its ''domain''. For example, the seismic waves generated by  For example, the sound pressure inside a recorder that is playing a "pure" note is typically a
For example, the sound pressure inside a recorder that is playing a "pure" note is typically a  * in the direction in space. For example, let the positive direction be to the right, and the negative direction be to the left.
* with constant
* in the direction in space. For example, let the positive direction be to the right, and the negative direction be to the left.
* with constant  The amplitude of a wave may be constant (in which case the wave is a ''c.w.'' or ''
The amplitude of a wave may be constant (in which case the wave is a ''c.w.'' or '' A standing wave, also known as a ''stationary wave'', is a wave whose
A standing wave, also known as a ''stationary wave'', is a wave whose  A soliton or solitary wave is a self-reinforcing
A soliton or solitary wave is a self-reinforcing 
 The analytical solution of SV-wave in a half-space indicates that the plane SV wave reflects back to the domain as a P and SV waves, leaving out special cases. The angle of the reflected SV wave is identical to the incidence wave, while the angle of the reflected P wave is greater than the SV wave. For the same wave frequency, the SV wavelength is smaller than the P wavelength. This fact has been depicted in this animated picture.
The analytical solution of SV-wave in a half-space indicates that the plane SV wave reflects back to the domain as a P and SV waves, leaving out special cases. The angle of the reflected SV wave is identical to the incidence wave, while the angle of the reflected P wave is greater than the SV wave. For the same wave frequency, the SV wavelength is smaller than the P wavelength. This fact has been depicted in this animated picture.
 Refraction is the phenomenon of a wave changing its speed. Mathematically, this means that the size of the
Refraction is the phenomenon of a wave changing its speed. Mathematically, this means that the size of the  Dispersion is the frequency dependence of the
Dispersion is the frequency dependence of the  * Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
*
* Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
* 