|
Heat Equation
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. As the prototypical parabolic partial differential equation, the heat equation is among the most widely studied topics in pure mathematics, and its analysis is regarded as fundamental to the broader field of partial differential equations. The heat equation can also be considered on Riemannian manifolds, leading to many geometric applications. Following work of Subbaramiah Minakshisundaram and Åke Pleijel, the heat equation is closely related with spectral geometry. A seminal nonlinear variant of the heat equation was introduced to differential geometry by James Eells and Joseph Sampson in 1964, inspiring the introduction of the Ricci flow by Richard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Eqn
In thermodynamics, heat is defined as the form of energy crossing the boundary of a thermodynamic system by virtue of a temperature difference across the boundary. A thermodynamic system does not ''contain'' heat. Nevertheless, the term is also often used to refer to the thermal energy contained in a system as a component of its internal energy and that is reflected in the temperature of the system. For both uses of the term, heat is a form of energy. An example of formal vs. informal usage may be obtained from the right-hand photo, in which the metal bar is "conducting heat" from its hot end to its cold end, but if the metal bar is considered a thermodynamic system, then the energy flowing within the metal bar is called internal energy, not heat. The hot metal bar is also transferring heat to its surroundings, a correct statement for both the strict and loose meanings of ''heat''. Another example of informal usage is the term '' heat content'', used despite the fact that p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard S
Richard is a male given name. It originates, via Old French, from Old Frankish and is a compound of the words descending from Proto-Germanic ''*rīk-'' 'ruler, leader, king' and ''*hardu-'' 'strong, brave, hardy', and it therefore means 'strong in rule'. Nicknames include " Richie", "Dick", " Dickon", " Dickie", "Rich", " Rick", " Rico", " Ricky", and more. Richard is a common English, German and French male name. It's also used in many more languages, particularly Germanic, such as Norwegian, Danish, Swedish, Icelandic, and Dutch, as well as other languages including Irish, Scottish, Welsh and Finnish. Richard is cognate with variants of the name in other European languages, such as the Swedish "Rickard", the Catalan "Ricard" and the Italian "Riccardo", among others (see comprehensive variant list below). People named Richard Multiple people with the same name * Richard Andersen (other) * Richard Anderson (other) * Richard Cartwright (disambiguati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of a wave function, the quantum-mechanical characterization of an isolated physical system. The equation can be derived from the fact that the time-evolution operator must be unitary, and must therefore be generated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Financial Mathematics
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often by help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on mathematical fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black–Scholes Equation
In mathematical finance, the Black–Scholes equation is a partial differential equation (PDE) governing the price evolution of a European call or European put under the Black–Scholes model. Broadly speaking, the term may refer to a similar PDE that can be derived for a variety of options, or more generally, derivatives. For a European call or put on an underlying stock paying no dividends, the equation is: :\frac + \frac\sigma^2 S^2 \frac + rS\frac - rV = 0 where ''V'' is the price of the option as a function of stock price ''S'' and time ''t'', ''r'' is the risk-free interest rate, and \sigma is the volatility of the stock. The key financial insight behind the equation is that, under the model assumption of a frictionless market, one can perfectly hedge the option by buying and selling the underlying asset in just the right way and consequently “eliminate risk". This hedge, in turn, implies that there is only one right price for the option, as returned by the Black–Schol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
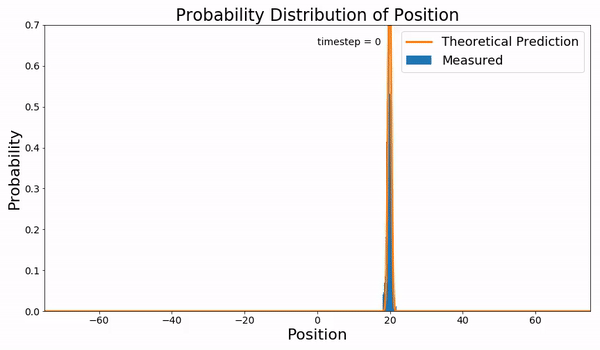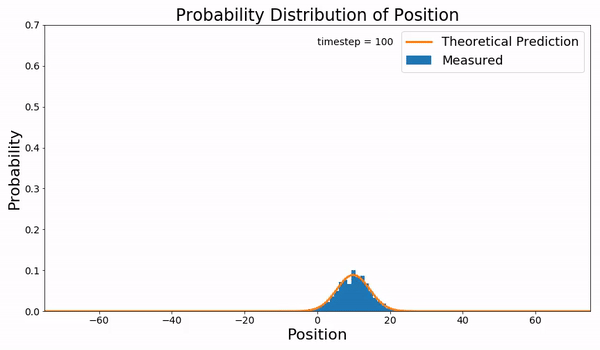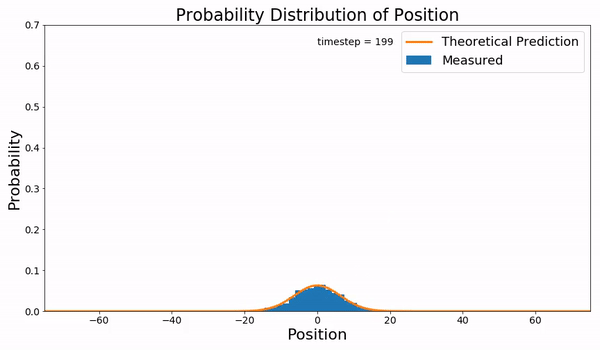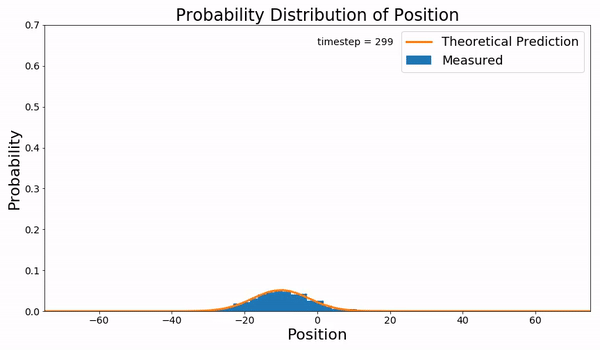
Brownian Motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas). This pattern of motion typically consists of random fluctuations in a particle's position inside a fluid sub-domain, followed by a relocation to another sub-domain. Each relocation is followed by more fluctuations within the new closed volume. This pattern describes a fluid at thermal equilibrium, defined by a given temperature. Within such a fluid, there exists no preferential direction of flow (as in transport phenomena). More specifically, the fluid's overall linear and angular momenta remain null over time. The kinetic energies of the molecular Brownian motions, together with those of molecular rotations and vibrations, sum up to the caloric component of a fluid's internal energy (the equipartition theorem). This motion is named after the botanist Robert Brown, who first described the phenomenon in 1827, while looking th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Lattice random walk A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of applied analysis, most notably differential equations; approximation theory (broadly construed, to include representations, asymptotic methods, variation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atiyah–Singer Index Theorem
In differential geometry, the Atiyah–Singer index theorem, proved by Michael Atiyah and Isadore Singer (1963), states that for an elliptic differential operator on a compact manifold, the analytical index (related to the dimension of the space of solutions) is equal to the topological index (defined in terms of some topological data). It includes many other theorems, such as the Chern–Gauss–Bonnet theorem and Riemann–Roch theorem, as special cases, and has applications to theoretical physics. History The index problem for elliptic differential operators was posed by Israel Gel'fand. He noticed the homotopy invariance of the index, and asked for a formula for it by means of topological invariants. Some of the motivating examples included the Riemann–Roch theorem and its generalization the Hirzebruch–Riemann–Roch theorem, and the Hirzebruch signature theorem. Friedrich Hirzebruch and Armand Borel had proved the integrality of the  genus of a spin manifold, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.png)