|
Fisher Kernel
In statistical classification, the Fisher kernel, named after Ronald Fisher, is a function that measures the similarity of two objects on the basis of sets of measurements for each object and a statistical model. In a classification procedure, the class for a new object (whose real class is unknown) can be estimated by minimising, across classes, an average of the Fisher kernel distance from the new object to each known member of the given class. The Fisher kernel was introduced in 1998. It combines the advantages of generative statistical models (like the hidden Markov model) and those of discriminative methods (like support vector machines): * generative models can process data of variable length (adding or removing data is well-supported) * discriminative methods can have flexible criteria and yield better results. Derivation Fisher score The Fisher kernel makes use of the Fisher score, defined as : U_X = \nabla_ \log P(X, \theta) with ''θ'' being a set (vector) of pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistical Classification
When classification is performed by a computer, statistical methods are normally used to develop the algorithm. Often, the individual observations are analyzed into a set of quantifiable properties, known variously as explanatory variables or ''features''. These properties may variously be categorical (e.g. "A", "B", "AB" or "O", for blood type), ordinal (e.g. "large", "medium" or "small"), integer-valued (e.g. the number of occurrences of a particular word in an email) or real-valued (e.g. a measurement of blood pressure). Other classifiers work by comparing observations to previous observations by means of a similarity or distance function. An algorithm that implements classification, especially in a concrete implementation, is known as a classifier. The term "classifier" sometimes also refers to the mathematical function, implemented by a classification algorithm, that maps input data to a category. Terminology across fields is quite varied. In statistics, where classi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fisher Information
In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable ''X'' carries about an unknown parameter ''θ'' of a distribution that models ''X''. Formally, it is the variance of the score, or the expected value of the observed information. The role of the Fisher information in the asymptotic theory of maximum-likelihood estimation was emphasized and explored by the statistician Sir Ronald Fisher (following some initial results by Francis Ysidro Edgeworth). The Fisher information matrix is used to calculate the covariance matrices associated with maximum-likelihood estimates. It can also be used in the formulation of test statistics, such as the Wald test. In Bayesian statistics, the Fisher information plays a role in the derivation of non-informative prior distributions according to Jeffreys' rule. It also appears as the large-sample covariance of the posterior distribution, provided that the prior i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bag-of-words Model In Computer Vision
In computer vision, the bag-of-words (BoW) model, sometimes called bag-of-visual-words model (BoVW), can be applied to image classification or retrieval, by treating image features as words. In document classification, a bag of words is a sparse vector of occurrence counts of words; that is, a sparse histogram over the vocabulary. In computer vision, a ''bag of visual words'' is a vector of occurrence counts of a vocabulary of local image features. Image representation based on the BoW model To represent an image using the BoW model, an image can be treated as a document. Similarly, "words" in images need to be defined too. To achieve this, it usually includes following three steps: feature detection, feature description, and codebook generation. A definition of the BoW model can be the "histogram representation based on independent features". Content based image indexing and retrieval (CBIR) appears to be the early adopter of this image representation technique. Featur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Feature (computer Vision)
In computer vision and image processing, a feature is a piece of information about the content of an image; typically about whether a certain region of the image has certain properties. Features may be specific structures in the image such as points, edges or objects. Features may also be the result of a general neighborhood operation or feature detection applied to the image. Other examples of features are related to motion in image sequences, or to shapes defined in terms of curves or boundaries between different image regions. More broadly a ''feature'' is any piece of information that is relevant for solving the computational task related to a certain application. This is the same sense as feature in machine learning and pattern recognition generally, though image processing has a very sophisticated collection of features. The feature concept is very general and the choice of features in a particular computer vision system may be highly dependent on the specific problem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bag Of Words Model In Computer Vision
In computer vision, the bag-of-words (BoW) model, sometimes called bag-of-visual-words model (BoVW), can be applied to image classification or retrieval, by treating image features as words. In document classification, a bag of words is a sparse vector of occurrence counts of words; that is, a sparse histogram over the vocabulary. In computer vision, a ''bag of visual words'' is a vector of occurrence counts of a vocabulary of local image features. Image representation based on the BoW model To represent an image using the BoW model, an image can be treated as a document. Similarly, "words" in images need to be defined too. To achieve this, it usually includes following three steps: feature detection, feature description, and codebook generation. A definition of the BoW model can be the "histogram representation based on independent features". Content based image indexing and retrieval (CBIR) appears to be the early adopter of this image representation technique. Feature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probabilistic Latent Semantic Analysis
Probabilistic latent semantic analysis (PLSA), also known as probabilistic latent semantic indexing (PLSI, especially in information retrieval circles) is a statistical technique for the analysis of two-mode and co-occurrence data. In effect, one can derive a low-dimensional representation of the observed variables in terms of their affinity to certain hidden variables, just as in latent semantic analysis, from which PLSA evolved. Compared to standard latent semantic analysis which stems from linear algebra and downsizes the occurrence tables (usually via a singular value decomposition), probabilistic latent semantic analysis is based on a mixture decomposition derived from a latent class model. Model Considering observations in the form of co-occurrences (w,d) of words and documents, PLSA models the probability of each co-occurrence as a mixture of conditionally independent multinomial distributions: : P(w,d) = \sum_c P(c) P(d, c) P(w, c) = P(d) \sum_c P(c, d) P(w, c) with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Naive Bayes
In statistics, naive (sometimes simple or idiot's) Bayes classifiers are a family of " probabilistic classifiers" which assumes that the features are conditionally independent, given the target class. In other words, a naive Bayes model assumes the information about the class provided by each variable is unrelated to the information from the others, with no information shared between the predictors. The highly unrealistic nature of this assumption, called the naive independence assumption, is what gives the classifier its name. These classifiers are some of the simplest Bayesian network models. Naive Bayes classifiers generally perform worse than more advanced models like logistic regressions, especially at quantifying uncertainty (with naive Bayes models often producing wildly overconfident probabilities). However, they are highly scalable, requiring only one parameter for each feature or predictor in a learning problem. Maximum-likelihood training can be done by evaluating a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
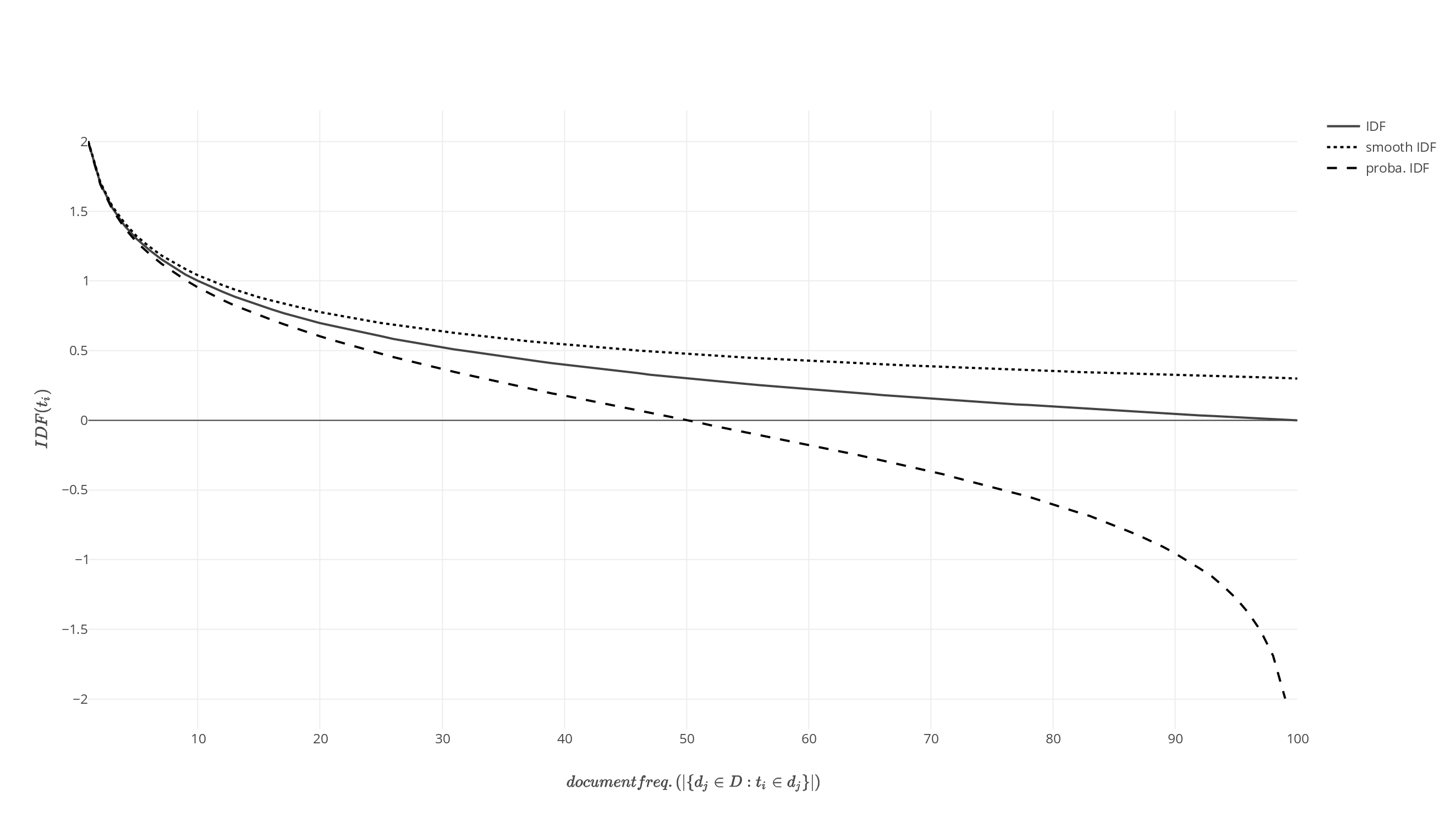
Tf–idf
In information retrieval, tf–idf (term frequency–inverse document frequency, TF*IDF, TFIDF, TF–IDF, or Tf–idf) is a measure of importance of a word to a document in a collection or Text corpus, corpus, adjusted for the fact that some words appear more frequently in general. Like the bag-of-words model, it models a document as a multiset of words, without word order. It is a refinement over the simple bag-of-words model, by allowing the weight of words to depend on the rest of the corpus. It was often used as a weighting factor in searches of information retrieval, text mining, and user modeling. A survey conducted in 2015 showed that 83% of text-based recommender systems in digital libraries used tf–idf. Variations of the tf–idf weighting scheme were often used by search engines as a central tool in scoring and ranking a document's Relevance (information retrieval), relevance given a user Information retrieval, query. One of the simplest ranking functions is computed b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Log-likelihood
A likelihood function (often simply called the likelihood) measures how well a statistical model explains observed data by calculating the probability of seeing that data under different parameter values of the model. It is constructed from the joint probability distribution of the random variable that (presumably) generated the observations. When evaluated on the actual data points, it becomes a function solely of the model parameters. In maximum likelihood estimation, the argument that maximizes the likelihood function serves as a point estimate for the unknown parameter, while the Fisher information (often approximated by the likelihood's Hessian matrix at the maximum) gives an indication of the estimate's precision. In contrast, in Bayesian statistics, the estimate of interest is the ''converse'' of the likelihood, the so-called posterior probability of the parameter given the observed data, which is calculated via Bayes' rule. Definition The likelihood function, paramet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, Fisher was the one to most comprehensively combine the ideas of Gregor Mendel and Charles Darwin, as his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the Modern synthesis (20th century), modern synthesis. For his contributions to biology, Richard Dawkins declared Fisher to be the greatest of Darwin's successors. He is also considered one of the founding fathers of Neo-Darwinism. According to statistician Jeffrey T. Leek, Fisher is the most in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Score (statistics)
In statistics, the score (or informant) is the gradient of the log-likelihood function with respect to the statistical parameter, parameter vector. Evaluated at a particular value of the parameter vector, the score indicates the steepness of the log-likelihood function and thereby the sensitivity to infinitesimal changes to the parameter values. If the log-likelihood function is Continuous function, continuous over the parameter space, the score will vanish (mathematics), vanish at a local Maxima and minima, maximum or minimum; this fact is used in maximum likelihood estimation to find the parameter values that maximize the likelihood function. Since the score is a function of the Realization (probability), observations, which are subject to sampling error, it lends itself to a test statistic known as ''score test'' in which the parameter is held at a particular value. Further, the likelihood ratio, ratio of two likelihood functions evaluated at two distinct parameter values can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Support Vector Machine
In machine learning, support vector machines (SVMs, also support vector networks) are supervised max-margin models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories, SVMs are one of the most studied models, being based on statistical learning frameworks of VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). In addition to performing linear classification, SVMs can efficiently perform non-linear classification using the ''kernel trick'', representing the data only through a set of pairwise similarity comparisons between the original data points using a kernel function, which transforms them into coordinates in a higher-dimensional feature space. Thus, SVMs use the kernel trick to implicitly map their inputs into high-dimensional feature spaces, where linear classification can be performed. Being max-margin models, SVMs are resilient to noisy data (e.g., misclassified examples). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |