|
Finite Volume Method For Two Dimensional Diffusion Problem
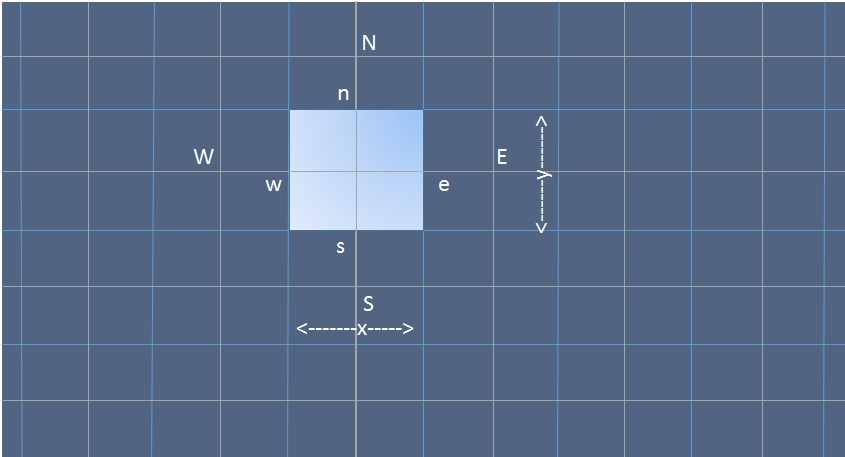
The methods used for solving two dimensional Diffusion problems are similar to those used for one dimensional problems. The general equation for steady diffusion can be easily derived from the general transport equation for property ''Φ'' by deleting transient and convective terms \frac\left(\Gamma\frac\right)+\frac\left(\Gamma\frac\right)+S=0 where, \Gamma is the Diffusion coefficient and S is the Source term. A portion of the two dimensional grid used for Discretization is shown below: In addition to the east (E) and west (W) neighbors, a general grid node P , now also has north (N) and south (S) neighbors. The same notation is used here for all faces and cell dimensions as in one dimensional analysis. When the above equation is formally integrated over the Control volume, we obtain \int_\frac\left(\Gamma\frac\right)dxdy+\int_\frac\left(\Gamma\frac\right)dxdy+\int_S_dV=0 Using the divergence theorem, the equation can be rewritten as : \left eA_e\left(\frac\right)_-_wA_w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon Mesh
In 3D computer graphics and solid modeling, a polygon mesh is a collection of , s and s that defines the shape of a polyhedral object. The faces usually consist of triangles ( triangle mesh), quadrilaterals (quads), or other simple convex polygons (n-gons), since this simplifies rendering, but may also be more generally composed of concave polygons, or even polygons with holes. The study of polygon meshes is a large sub-field of computer graphics (specifically 3D computer graphics) and geometric modeling. Different representations of polygon meshes are used for different applications and goals. The variety of operations performed on meshes may include: Boolean logic ( Constructive solid geometry), smoothing, simplification, and many others. Algorithms also exist for ray tracing, collision detection, and rigid-body dynamics with polygon meshes. If the mesh's edges are rendered instead of the faces, then the model becomes a wireframe model. Volumetric meshes are di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discretization
In applied mathematics, discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers. Dichotomization is the special case of discretization in which the number of discrete classes is 2, which can approximate a continuous variable as a binary variable (creating a dichotomy for modeling purposes, as in binary classification). Discretization is also related to discrete mathematics, and is an important component of granular computing. In this context, ''discretization'' may also refer to modification of variable or category ''granularity'', as when multiple discrete variables are aggregated or multiple discrete categories fused. Whenever continuous data is discretized, there is always some amount of discretization error. The goal is to reduce the amount to a level c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cfd Graph
__NOTOC__ CFD may refer to: Science and computing * Computational fluid dynamics, a branch of fluid mechanics using computational methods to predict the behavior of fluid flows * Counterfactual definiteness, the ability, in quantum mechanics, to consider results of unperformed measurements * CFEngine daemon, the process that runs CFEngine * Common fill device, an electronic module used to load cryptographic keys into electronic encryption machines * Constant fraction discriminator, a signal processing component * Complement factor D, an enzyme encoded by the ''CFD'' gene Business * Contract for difference, a type of financial derivative, where two parties exchange the difference between opening and closing value of an underlying asset * Control Flow Diagram, is a diagram to describe the control flow of a business process, process or program * Cumulative Flow Diagram, an area graph that depicts the quantity of work in a given state Firefighting organizations * Calgary F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Volume
In continuum mechanics and thermodynamics, a control volume (CV) is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fictitious region of a given volume fixed in space or moving with constant flow velocity through which the continuum ( gas, liquid or solid) flows. The closed surface enclosing the region is referred to as the control surface. At steady state, a control volume can be thought of as an arbitrary volume in which the mass of the continuum remains constant. As a continuum moves through the control volume, the mass entering the control volume is equal to the mass leaving the control volume. At steady state, and in the absence of work and heat transfer, the energy within the control volume remains constant. It is analogous to the classical mechanics concept of the free body diagram. Overview Typically, to understand how a given physical law applies to the system under con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface. Terminology The word ''flux'' comes from Latin: ''fluxus'' means "flow", and ''fluere'' is "to flow". As '' fluxion'', this term was introduced into differential calculus by Isaac Newton. The concept of heat flux was a key contribution of Joseph Fourier, in the analysis of heat transfer phenomena. His seminal treatise ''Théorie analytique de la chaleur'' (''The Analytical Theory of Heat''), defines ''fluxion'' as a central quantity and proceeds to derive the now well-known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Value Problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial different ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's laws of diffusion). In mathematics, it is related to Markov processes, such as random walks, and applied in many other fields, such as materials science, information theory, and biophysics. The diffusion equation is a special case of the convection–diffusion equation, when bulk velocity is zero. It is equivalent to the heat equation under some circumstances. Statement The equation is usually written as: where is the density of the diffusing material at location and time and is the collective diffusion coefficient for density at location ; and represents the vector differential operator del. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. The equation above applies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Fluid Dynamics
Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid ( liquids and gases) with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests. CFD is appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection–diffusion Equation
The convection–diffusion equation is a combination of the diffusion and convection (advection) equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift–diffusion equation, or (generic) scalar transport equation. Equation General The general equation is \frac = \mathbf \cdot (D \mathbf c) - \mathbf \cdot (\mathbf c) + R where * is the variable of interest (species concentration for mass transfer, temperature for heat transfer), * is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport, * is the velocity field that the quantity is moving with. It is a function of time and space. For example, in advection, might be the concentration of salt in a river, and then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Difference
A finite difference is a mathematical expression of the form . If a finite difference is divided by , one gets a difference quotient. The approximation of derivatives by finite differences plays a central role in finite difference methods for the numerical solution of differential equations, especially boundary value problems. The difference operator, commonly denoted \Delta is the operator that maps a function to the function \Delta /math> defined by :\Delta x)= f(x+1)-f(x). A difference equation is a functional equation that involves the finite difference operator in the same way as a differential equation involves derivatives. There are many similarities between difference equations and differential equations, specially in the solving methods. Certain recurrence relations can be written as difference equations by replacing iteration notation with finite differences. In numerical analysis, finite differences are widely used for approximating derivatives, and the term ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |