Convection–diffusion Equation

The convection–diffusion equation is a combination of the diffusion and convection (advection) equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift–diffusion equation, or (generic) scalar transport equation.

Equation

General

The general equation is
$\frac = \mathbf \cdot (D \mathbf c) - \mathbf \cdot (\mathbf c) + R$
where
* is the variable of interest (species concentration for mass transfer, temperature for heat transfer),
* is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport,
* is the velocity field that the quantity is moving with. It is a function of time and space. For example, in advection, might be the concentration of salt in a river, and then would be the velocity of the water flow as a function of time and location. Another example, might be the concentration of small bubbles in a calm lake, and then would be the velocity of bubbles rising towards the surface by buoyancy (see below) depending on time and location of the bubble. For multiphase flows and flows in porous media, is the (hypothetical) superficial velocity.
* describes sources or sinks of the quantity . For example, for a chemical species, means that a chemical reaction is creating more of the species, and means that a chemical reaction is destroying the species. For heat transport, might occur if thermal energy is being generated by friction.
* represents gradient and represents divergence. In this equation, represents concentration gradient.

Understanding the terms involved

The right-hand side of the equation is the sum of three contributions.
* The first, , describes diffusion. Imagine that is the concentration of a chemical. When concentration is low somewhere compared to the surrounding areas (e.g. a local minimum of concentration), the substance will diffuse in from the surroundings, so the concentration will increase. Conversely, if concentration is high compared to the surroundings (e.g. a local maximum of concentration), then the substance will diffuse out and the concentration will decrease. The net diffusion is proportional to the Laplacian (or second derivative) of concentration if the diffusivity is a constant.
* The second contribution, , describes convection (or advection). Imagine standing on the bank of a river, measuring the water's salinity (amount of salt) each second. Upstream, somebody dumps a bucket of salt into the river. A while later, you would see the salinity suddenly rise, then fall, as the zone of salty water passes by. Thus, the concentration ''at a given location'' can change because of the flow.
* The final contribution, , describes the creation or destruction of the quantity. For example, if is the concentration of a molecule, then describes how the molecule can be created or destroyed by chemical reactions. may be a function of and of other parameters. Often there are several quantities, each with its own convection–diffusion equation, where the destruction of one quantity entails the creation of another. For example, when methane burns, it involves not only the destruction of methane and oxygen but also the creation of carbon dioxide and water vapor. Therefore, while each of these chemicals has its own convection–diffusion equation, they are coupled together and must be solved as a system of ''simultaneous'' differential equations.

Common simplifications

In a common situation, the diffusion coefficient is constant, there are no sources or sinks, and the velocity field describes an incompressible flow (i.e., it has zero divergence). Then the formula simplifies to:
$\frac = D \nabla^2 c - \mathbf \cdot \nabla c.$

In this form, the convection–diffusion equation combines both parabolic and hyperbolic partial differential equations.

In non-interacting material, (for example, when temperature is close to absolute zero, dilute gas has almost zero mass diffusivity), hence the transport equation is simply:
$\frac + \mathbf \cdot \nabla c=0.$

Using Fourier transform in both temporal and spatial domain (that is, with integral kernel $e^$), its characteristic equation can be obtained:
$j\omega \tilde c+\mathbf\cdot j \mathbf \tilde c=0 \rightarrow \omega=-\mathbf\cdot \mathbf,$
which gives the general solution:
$c=f(\mathbf-\mathbft),$
where $f$ is any differentiable scalar function. This is the basis of temperature measurement for ''near'' Bose–Einstein condensate via time of flight method.

Stationary version

The stationary convection–diffusion equation describes the steady-state behavior of a convective-diffusive system. In a steady state, , so the formula is:
$0 = \nabla \cdot (D \nabla c) - \nabla \cdot (\mathbf c) + R.$

Derivation

The convection–diffusion equation can be derived in a straightforward way from the continuity equation, which states that the rate of change for a scalar quantity in a differential control volume is given by flow and diffusion into and out of that part of the system along with any generation or consumption inside the control volume:
$\frac + \nabla\cdot\mathbf = R,$
where is the total flux and is a net volumetric source for . There are two sources of flux in this situation. First, diffusive flux arises due to diffusion. This is typically approximated by Fick's first law:
$\mathbf_\text = -D \nabla c$
i.e., the flux of the diffusing material (relative to the bulk motion) in any part of the system is proportional to the local concentration gradient. Second, when there is overall convection or flow, there is an associated flux called advective flux:
$\mathbf_\text = \mathbf c$
The total flux (in a stationary coordinate system) is given by the sum of these two:
$\mathbf = \mathbf_\text + \mathbf_\text = -D \nabla c + \mathbf c.$
Plugging into the continuity equation:
$\frac + \nabla\cdot \left(-D \nabla c + \mathbf c \right) = R.$

Complex mixing phenomena

In general, , , and may vary with space and time. In cases in which they depend on concentration as well, the equation becomes nonlinear, giving rise to many distinctive mixing phenomena such as Rayleigh–Bénard convection when depends on temperature in the heat transfer formulation and reaction–diffusion pattern formation when depends on concentration in the mass transfer formulation.

Velocity in response to a force

In some cases, the average velocity field exists because of a force; for example, the equation might describe the flow of ions dissolved in a liquid, with an electric field pulling the ions in some direction (as in gel electrophoresis). In this situation, it is usually called the drift–diffusion equation or the Smoluchowski equation, See equation (312) after Marian Smoluchowski who described it in 1915 (not to be confused with the Einstein–Smoluchowski relation or Smoluchowski coagulation equation).

Typically, the average velocity is directly proportional to the applied force, giving the equation:
:$\frac = \nabla \cdot (D \nabla c) - \nabla \cdot \left( \zeta^ \mathbf c \right) + R$
where is the force, and characterizes the friction or viscous drag. (The inverse is called mobility.)

Derivation of Einstein relation

When the force is associated with a potential energy (see conservative force), a steady-state solution to the above equation (i.e. ) is:
:$c \propto \exp \left( -D^ \zeta^ U \right)$
(assuming and are constant). In other words, there are more particles where the energy is lower. This concentration profile is expected to agree with the Boltzmann distribution (more precisely, the Gibbs measure). From this assumption, the Einstein relation can be proven:
:$D \zeta = k_\mathrm T.$

Smoluchowski convection-diffusion equation

The Smoluchowski convective-diffusion equation is a stochastic (Smoluchowski) diffusion equation with an additional convective flow-field,
:$\frac = \nabla \cdot (D \nabla c) - \mathbf \cdot (\mathbf c) - \nabla \cdot \left( \zeta^ \mathbf c \right)$
In this case, the force describes the conservative interparticle interaction force between two colloidal particles or the intermolecular interaction force between two molecules in the fluid, and it is unrelated to the externally imposed flow velocity . The steady-state version of this equation is the basis to provide a description of the pair distribution function (which can be identified with ) of colloidal suspensions under shear flows.

An approximate solution to the steady-state version of this equation has been found using the method of matched asymptotic expansions. This solution provides a theory for the transport-controlled reaction rate of two molecules in a shear flow, and also provides a way to extend the DLVO theory of colloidal stability to colloidal systems subject to shear flows (e.g. in microfluidics, chemical reactors, environmental flows).
The full solution to the steady-state equation, obtained using the method of matched asymptotic expansions, has been developed by Alessio Zaccone and L. Banetta to compute the pair distribution function of Lennard-Jones interacting particles in shear flow and subsequently extended to compute the pair distribution function of charge-stabilized (Yukawa or Debye–Hückel) colloidal particles in shear flows.

As a stochastic differential equation

The convection–diffusion equation (with no sources or drains, ) can be viewed as a stochastic differential equation, describing random motion with diffusivity and bias . For example, the equation can describe the Brownian motion of a single particle, where the variable describes the probability distribution for the particle to be in a given position at a given time. The reason the equation can be used that way is because there is no mathematical difference between the probability distribution of a single particle, and the concentration profile of a collection of infinitely many particles (as long as the particles do not interact with each other).

The ''Langevin equation'' describes advection, diffusion, and other phenomena in an explicitly stochastic way. One of the simplest forms of the Langevin equation is when its "noise term" is Gaussian; in this case, the Langevin equation is exactly equivalent to the convection–diffusion equation. However, the Langevin equation is more general.

Numerical solution

The convection–diffusion equation can only rarely be solved with a pen and paper. More often, computers are used to numerically approximate the solution to the equation, typically using the finite element method. For more details and algorithms see: Numerical solution of the convection–diffusion equation.

Similar equations in other contexts

The convection–diffusion equation is a relatively simple equation describing flows, or alternatively, describing a stochastically-changing system. Therefore, the same or similar equation arises in many contexts unrelated to flows through space.
*It is formally identical to the Fokker–Planck equation for the velocity of a particle.
*It is closely related to the Black–Scholes equation and other equations in financial mathematics.
*It is closely related to the Navier–Stokes equations, because the flow of momentum in a fluid is mathematically similar to the flow of mass or energy. The correspondence is clearest in the case of an incompressible Newtonian fluid, in which case the Navier–Stokes equation is: $\frac = \mu \nabla^2 \mathbf -\mathbf \cdot \nabla \mathbf + (\mathbf-\nabla P)$
where is the momentum of the fluid (per unit volume) at each point (equal to the density multiplied by the velocity ), is viscosity, is fluid pressure, and is any other body force such as gravity. In this equation, the term on the left-hand side describes the change in momentum at a given point; the first term on the right describes the diffusion of momentum by viscosity; the second term on the right describes the advective flow of momentum; and the last two terms on the right describes the external and internal forces which can act as sources or sinks of momentum.

In semiconductor physics

In semiconductor physics, this equation is called the drift–diffusion equation. The word "drift" is related to drift current and drift velocity. The equation is normally written:
:$\begin \frac &= - D_n \nabla n - n \mu_n \mathbf \\ \frac &= - D_p \nabla p + p \mu_p \mathbf \\ \frac &= -\nabla \cdot \frac + R \\ \frac &= -\nabla \cdot \frac + R \end$
where
* and are the concentrations (densities) of electrons and holes, respectively,
* is the elementary charge,
* and are the electric currents due to electrons and holes respectively,
* and are the corresponding "particle currents" of electrons and holes respectively,
* represents carrier generation and recombination ( for generation of electron-hole pairs, for recombination.)
* is the electric field vector
*$\mu_n$ and $\mu_p$ are electron and hole mobility.

The diffusion coefficient and mobility are related by the Einstein relation as above:
:$\begin D_n &= \frac, \\ D_p &= \frac, \end$
where is the Boltzmann constant and is absolute temperature. The drift current and diffusion current refer separately to the two terms in the expressions for , namely:
:$\begin \frac &= - n \mu_n \mathbf, \\ \frac &= p \mu_p \mathbf, \\ \frac &= - D_n \nabla n, \\ \frac &= - D_p \nabla p. \end$

This equation can be solved together with Poisson's equation numerically.

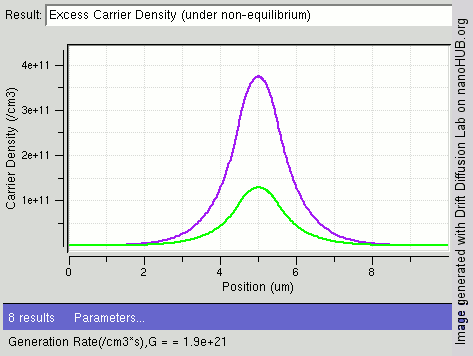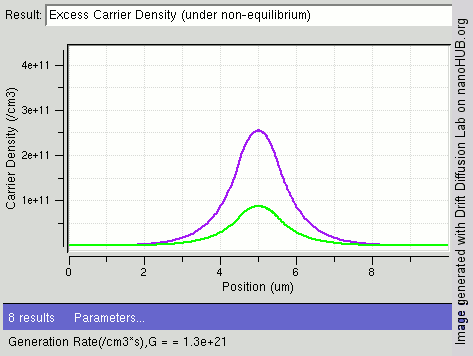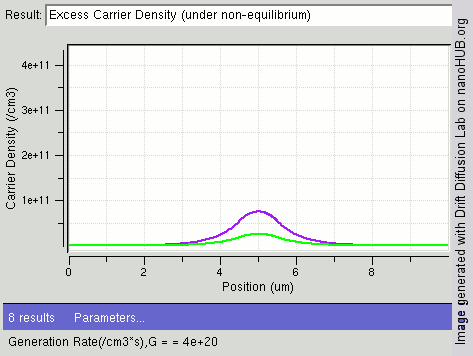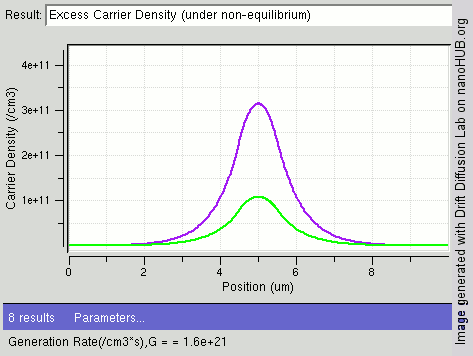
An example of results of solving the drift diffusion equation is shown on the right. When light shines on the center of semiconductor, carriers are generated in the middle and diffuse towards two ends. The drift–diffusion equation is solved in this structure and electron density distribution is displayed in the figure. One can see the gradient of carrier from center towards two ends.

See also

* Advanced Simulation Library
* Conservation equations
* Incompressible Navier–Stokes equations
* Nernst–Planck equation
* Double diffusive convection
* Natural convection
* Buckley–Leverett equation

References

Further reading

*

{{DEFAULTSORT:Convection-diffusion equation
Diffusion
Parabolic partial differential equations
Stochastic differential equations
Transport phenomena
Equations of physics