|
Buckley–Leverett Equation
In fluid dynamics, the Buckley–Leverett equation is a conservation equation used to model two-phase flow in porous media. The Buckley–Leverett equation or the Buckley–Leverett ''displacement'' describes an immiscible displacement process, such as the displacement of oil by water, in a one-dimensional or quasi-one-dimensional reservoir. This equation can be derived from the mass conservation equations of two-phase flow, under the assumptions listed below. Equation In a quasi-1D domain, the Buckley–Leverett equation is given by: : \frac + \frac\left( \frac f_w(S_w) \right) = 0, where S_w(x,t) is the wetting-phase (water) saturation, Q is the total flow rate, \phi is the rock porosity, A is the area of the cross-section in the sample volume, and f_w(S_w) is the fractional flow function of the wetting phase. Typically, f_w(S_w) is an 'S'-shaped, nonlinear function of the saturation S_w, which characterizes the relative mobilities of the two phases: : f_w(S_w) = \frac = \fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including '' aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
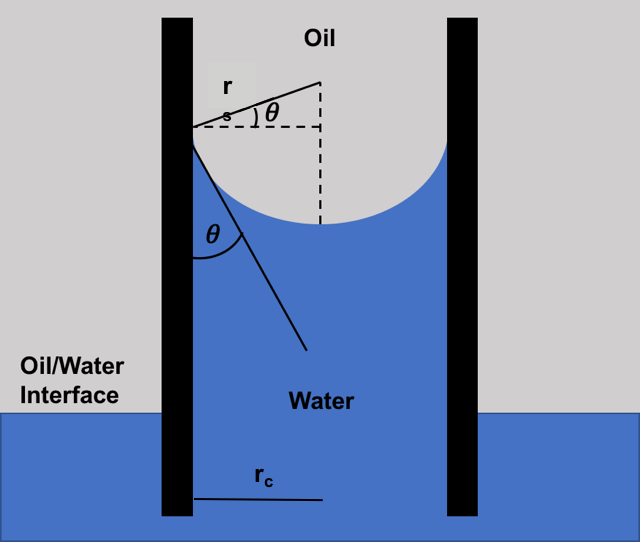
Capillary Pressure
In fluid statics, capillary pressure () is the pressure between two immiscible fluids in a thin tube (see capillary action), resulting from the interactions of forces between the fluids and solid walls of the tube. Capillary pressure can serve as both an opposing or driving force for fluid transport and is a significant property for research and industrial purposes (namely microfluidic design and oil extraction from porous rock). It is also observed in natural phenomena. Definition Capillary pressure is defined as: :p_c=p_-p_ where: :p_is the capillary pressure :p_ is the pressure of the non-wetting phase :p_ is the pressure of the wetting phase The wetting phase is identified by its ability to preferentially diffuse across the capillary walls before the non-wetting phase. The "wettability" of a fluid depends on its surface tension, the forces that drive a fluid's tendency to take up the minimal amount of space possible, and it is determined by the contact angle of the fluid.Fan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darcy's Law
Darcy's law is an equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on results of experiments on the flow of water through beds of sand, forming the basis of hydrogeology, a branch of earth sciences. It is analogous to Ohm's law in electrostatics, linearly relating the volume flow rate of the fluid to the hydraulic head difference (which is often just proportional to the pressure difference) via the hydraulic conductivity. Background Darcy's law was first determined experimentally by Darcy, but has since been derived from the Navier–Stokes equations via homogenization methods. It is analogous to Fourier's law in the field of heat conduction, Ohm's law in the field of electrical networks, and Fick's law in diffusion theory. One application of Darcy's law is in the analysis of water flow through an aquifer; Darcy's law along with the equation of conservation of mass simplifies to the groundwater flow equation, on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Permeability
In multiphase flow in porous media, the relative permeability of a phase is a dimensionless measure of the effective permeability of that phase. It is the ratio of the effective permeability of that phase to the absolute permeability. It can be viewed as an adaptation of Darcy's law to multiphase flow. For two-phase flow in porous media given steady-state conditions, we can write :q_i = -\frac \nabla P_i \qquad \text \quad i=1,2 where q_i is the flux, \nabla P_i is the pressure drop, \mu_i is the viscosity. The subscript i indicates that the parameters are for phase i. k_i is here the phase permeability (i.e., the effective permeability of phase i), as observed through the equation above. Relative permeability, k_, for phase i is then defined from k_i = k_k, as :k_ = k_i / k where k is the permeability of the porous medium in single-phase flow, i.e., the absolute permeability. Relative permeability must be between zero and one. In applications, relative permeability is of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capillary Pressure
In fluid statics, capillary pressure () is the pressure between two immiscible fluids in a thin tube (see capillary action), resulting from the interactions of forces between the fluids and solid walls of the tube. Capillary pressure can serve as both an opposing or driving force for fluid transport and is a significant property for research and industrial purposes (namely microfluidic design and oil extraction from porous rock). It is also observed in natural phenomena. Definition Capillary pressure is defined as: :p_c=p_-p_ where: :p_is the capillary pressure :p_ is the pressure of the non-wetting phase :p_ is the pressure of the wetting phase The wetting phase is identified by its ability to preferentially diffuse across the capillary walls before the non-wetting phase. The "wettability" of a fluid depends on its surface tension, the forces that drive a fluid's tendency to take up the minimal amount of space possible, and it is determined by the contact angle of the fluid.Fan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rarefaction
Rarefaction is the reduction of an item's density, the opposite of compression. Like compression, which can travel in waves ( sound waves, for instance), rarefaction waves also exist in nature. A common rarefaction wave is the area of low relative pressure following a shock wave (see picture). Rarefaction waves expand with time (much like sea waves spread out as they reach a beach); in most cases rarefaction waves keep the same overall profile ('shape') at all times throughout the wave's movement: it is a ''self-similar expansion''. Each part of the wave travels at the local speed of sound, in the local medium. This expansion behaviour contrasts with that of pressure increases, which gets narrower with time until they steepen into shock waves. When angle of incidence is greater than angle of refraction, then light travels from denser to rarer medium. When angle of incidence is smaller than angle of refraction then light travels from rarer to denser medium Physical examples A n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shock Wave
In physics, a shock wave (also spelled shockwave), or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a medium but is characterized by an abrupt, nearly discontinuous, change in pressure, temperature, and density of the medium. For the purpose of comparison, in supersonic flows, additional increased expansion may be achieved through an expansion fan, also known as a Prandtl–Meyer expansion fan. The accompanying expansion wave may approach and eventually collide and recombine with the shock wave, creating a process of destructive interference. The sonic boom associated with the passage of a supersonic aircraft is a type of sound wave produced by constructive interference. Unlike solitons (another kind of nonlinear wave), the energy and speed of a shock wave alone dissipates relatively quickly with distance. When a shock wave passes thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Partial Differential Equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation (PDE) that, roughly speaking, has a well-posed initial value problem for the first n-1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation. In one spatial dimension, this is : \frac = c^2 \frac The equation has the property that, if ''u'' and its first time derivative are arbitrarily specified initial data on the line (with sufficient smoothness properties), then there exists a solution for all time ''t''. The solutions of hyperbolic equations are "wave-like". If a disturbance is made in the initial data of a hyperbolic differential equation, then not every point of space feels the disturbance at once. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Immiscible
Miscibility () is the property of two substances to mix in all proportions (that is, to fully dissolve in each other at any concentration), forming a homogeneous mixture (a solution). The term is most often applied to liquids but also applies to solids and gases. For example, water and ethanol are miscible because they mix in all proportions. By contrast, substances are said to be immiscible if there are certain proportions in which the mixture does not form a solution. For one example, oil is not soluble in water, so these two solvents are immiscible. As another example, butanone (methyl ethyl ketone) is significantly soluble in water, but these two solvents are also immiscible because in some proportions the mixture will separate into two phases. Organic compounds In organic compounds, the weight percent of hydrocarbon chain often determines the compound's miscibility with water. For example, among the alcohols, ethanol has two carbon atoms and is miscible with water, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of energy, conservation of linear momentum, conservation of angular momentum, and conservation of electric charge. There are also many approximate conservation laws, which apply to such quantities as mass, parity, lepton number, baryon number, strangeness, hypercharge, etc. These quantities are conserved in certain classes of physics processes, but not in all. A local conservation law is usually expressed mathematically as a continuity equation, a partial differential equation which gives a relation between the amount of the quantity and the "transport" of that quantity. It states that the amount of the conserved quantity at a point or within a volume can only change by the amount of the quantity which flows in or out of the volume. From Noether's theorem, each conservation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incompressible
In fluid mechanics or more generally continuum mechanics, incompressible flow ( isochoric flow) refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero (see the derivation below, which illustrates why these conditions are equivalent). Incompressible flow does not imply that the fluid itself is incompressible. It is shown in the derivation below that (under the right conditions) even compressible fluids can – to a good approximation – be modelled as an incompressible flow. Incompressible flow implies that the density remains constant within a parcel of fluid that moves with the flow velocity. Derivation The fundamental requirement for incompressible flow is that the density, \rho , is constant within a small element volume, ''dV'', which moves at the flow velocity u. Mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |