|
Advection Equation
In the fields of physics, engineering, and earth sciences, advection is the transport of a substance or quantity by bulk motion of a fluid. The properties of that substance are carried with it. Generally the majority of the advected substance is also a fluid. The properties that are carried with the advected substance are conserved properties such as energy. An example of advection is the transport of pollutants or silt in a river by bulk water flow downstream. Another commonly advected quantity is energy or enthalpy. Here the fluid may be any material that contains thermal energy, such as water or air. In general, any substance or conserved extensive quantity can be advected by a fluid that can hold or contain the quantity or substance. During advection, a fluid transports some conserved quantity or material via bulk motion. The fluid's motion is described mathematically as a vector field, and the transported material is described by a scalar field showing its distribution ove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
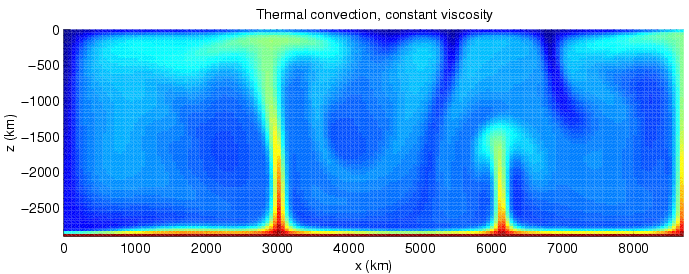
Convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss's Theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem relating the ''flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region enclosed by the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region". The divergence theorem is an important result for the mathematics of physics and engineering, particularly in electrostatics and fluid dynamics. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to the fundamental theorem of calcul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of mass-energy, conservation of linear momentum, conservation of angular momentum, and conservation of electric charge. There are also many approximate conservation laws, which apply to such quantities as mass, parity, lepton number, baryon number, strangeness, hypercharge, etc. These quantities are conserved in certain classes of physics processes, but not in all. A local conservation law is usually expressed mathematically as a continuity equation, a partial differential equation which gives a relation between the amount of the quantity and the "transport" of that quantity. It states that the amount of the conserved quantity at a point or within a volume can only change by the amount of the quantity which flows in or out of the volume. From Noether's theorem, every differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Velocity Field
In continuum mechanics the flow velocity in fluid dynamics, also macroscopic velocity in statistical mechanics, or drift velocity in electromagnetism, is a vector field used to mathematically describe the motion of a continuum. The length of the flow velocity vector is scalar, the ''flow speed''. It is also called velocity field; when evaluated along a line, it is called a velocity profile (as in, e.g., law of the wall). Definition The flow velocity ''u'' of a fluid is a vector field : \mathbf=\mathbf(\mathbf,t), which gives the velocity of an '' element of fluid'' at a position \mathbf\, and time t.\, The flow speed ''q'' is the length of the flow velocity vector :q = \, \mathbf \, and is a scalar field. Uses The flow velocity of a fluid effectively describes everything about the motion of a fluid. Many physical properties of a fluid can be expressed mathematically in terms of the flow velocity. Some common examples follow: Steady flow The flow of a fluid is sai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Partial Differential Equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation (PDE) that, roughly speaking, has a well-posed initial value problem for the first n - 1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of ... are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation. In one spatial dimension, this is \frac = c^2 \frac The equation has the property that, if and its first time derivative are arbitrarily specified initial data on the line (with sufficient smoothness properties), th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrological Cycle
The water cycle (or hydrologic cycle or hydrological cycle) is a biogeochemical cycle that involves the continuous movement of water on, above and below the surface of the Earth across different reservoirs. The mass of water on Earth remains fairly constant over time. However, the partitioning of the water into the major reservoirs of ice, fresh water, salt water and atmospheric water is variable and depends on climatic variables. The water moves from one reservoir to another, such as from river to ocean, or from the ocean to the atmosphere due to a variety of physical and chemical processes. The processes that drive these movements, or fluxes, are evaporation, transpiration, condensation, precipitation, sublimation, infiltration, surface runoff, and subsurface flow. In doing so, the water goes through different phases: liquid, solid (ice) and vapor. The ocean plays a key role in the water cycle as it is the source of 86% of global evaporation. The water cycle is driven by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orographic
Orography is the study of the topographic relief of mountains, and can more broadly include hills, and any part of a region's elevated terrain. Orography (also known as ''oreography'', ''orology,'' or ''oreology'') falls within the broader discipline of geomorphology. The term orography comes from the Greek: , hill, , to write. Uses Mountain ranges and elevated land masses have a major impact on global climate. For instance, the elevated areas of East Africa substantially determine the strength of the Indian monsoon.Srinivasan, J., Nanjundiah, Ravi S. and Chakraborty, Arindam (2005)"Impact of Orography on the Simulation of Monsoon Climate in a General Circulation Model" Indian Institute of Science. In scientific models, such as general circulation models, orography defines the lower boundary of the model over land. When a river's tributaries or settlements by the river are listed in 'orographic sequence', they are in order from the highest (nearest the source of the river) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horizontal Plane
Horizontal may refer to: *Horizontal plane, in astronomy, geography, geometry and other sciences and contexts *Horizontal coordinate system, in astronomy *Horizontalism, in monetary circuit theory *Horizontalidad, Horizontalism, in sociology *Horizontal market, in microeconomics *Horizontal (album), ''Horizontal'' (album), a 1968 album by the Bee Gees **Horizontal (song), "Horizontal" (song)" is a 1968 song by the Bee Gees See also *Horizontal and vertical *Horizontal and vertical (other) *Horizontal fissure (other), anatomical features *Horizontal bar, an apparatus used by male gymnasts in artistic gymnastics *Vertical (other) * {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
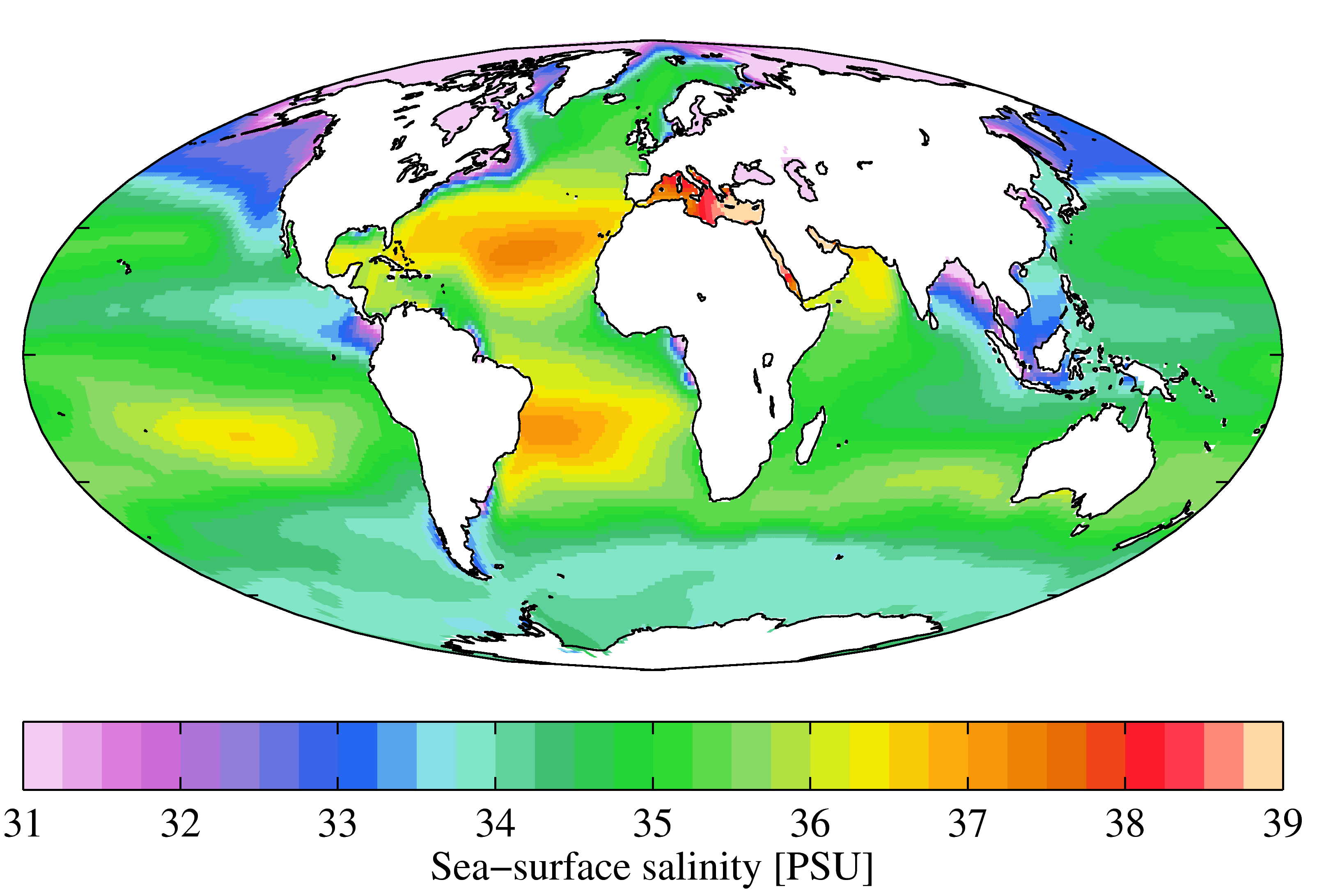
Salinity
Salinity () is the saltiness or amount of salt (chemistry), salt dissolved in a body of water, called saline water (see also soil salinity). It is usually measured in g/L or g/kg (grams of salt per liter/kilogram of water; the latter is dimensionless and equal to per mille, ‰). Salinity is an important factor in determining many aspects of the chemistry of natural waters and of biological processes within it, and is a state function, thermodynamic state variable that, along with temperature and pressure, governs physical characteristics like the density and heat capacity of the water. A contour line of constant salinity is called an ''isohaline'', or sometimes ''isohale''. Definitions Salinity in rivers, lakes, and the ocean is conceptually simple, but technically challenging to define and measure precisely. Conceptually the salinity is the quantity of dissolved salt content of the water. Salts are compounds like sodium chloride, magnesium sulfate, potassium nitrate, and sod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Water Vapor
Water vapor, water vapour, or aqueous vapor is the gaseous phase of Properties of water, water. It is one Phase (matter), state of water within the hydrosphere. Water vapor can be produced from the evaporation or boiling of liquid water or from the Sublimation (phase transition), sublimation of ice. Water vapor is transparent, like most constituents of the atmosphere. Under typical atmospheric conditions, water vapor is continuously generated by evaporation and removed by condensation. It is less dense than most of the other constituents of air and triggers convection currents that can lead to clouds and fog. Being a component of Earth's hydrosphere and hydrologic cycle, it is particularly abundant in Earth's atmosphere, where it acts as a greenhouse gas and warming feedback, contributing more to total greenhouse effect than non-condensable gases such as carbon dioxide and methane. Use of water vapor, as steam, has been important for cooking, and as a major component in energy prod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat
In thermodynamics, heat is energy in transfer between a thermodynamic system and its surroundings by such mechanisms as thermal conduction, electromagnetic radiation, and friction, which are microscopic in nature, involving sub-atomic, atomic, or molecular particles, or small surface irregularities, as distinct from the macroscopic modes of energy transfer, which are thermodynamic work and transfer of matter. For a closed system (transfer of matter excluded), the heat involved in a process is the difference in internal energy between the final and initial states of a system, after subtracting the work done in the process. For a closed system, this is the formulation of the first law of thermodynamics. Calorimetry is measurement of quantity of energy transferred as heat by its effect on the states of interacting bodies, for example, by the amount of ice melted or by change in temperature of a body. In the International System of Units (SI), the unit of measurement for he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |