|
Double Diffusive Convection
Double diffusive convection is a fluid dynamics phenomenon that describes a form of convection driven by two different density gradients, which have different rates of diffusion. Convection in fluids is driven by density variations within them under the influence of gravity. These density variations may be caused by gradients in the composition of the fluid, or by differences in temperature (through thermal expansion). Thermal and compositional gradients can often diffuse with time, reducing their ability to drive the convection, and requiring that gradients in other regions of the flow exist in order for convection to continue. A common example of double diffusive convection is in oceanography, where heat and salt concentrations exist with different gradients and diffuse at differing rates. An effect that affects both of these variables is the input of cold freshwater from an iceberg. Another example of double diffusion is the formation of false bottoms at the interface of sea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Salt Fingers
In common usage, salt is a mineral composed primarily of sodium chloride (NaCl). When used in food, especially in granulated form, it is more formally called table salt. In the form of a natural crystalline mineral, salt is also known as rock salt or halite. Salt is essential for life in general (being the source of the essential dietary minerals sodium and chlorine), and saltiness is one of the basic human tastes. Salt is one of the oldest and most ubiquitous food seasonings, and is known to uniformly improve the taste perception of food. Salting, brining, and pickling are ancient and important methods of food preservation. Some of the earliest evidence of salt processing dates to around 6000 BC, when people living in the area of present-day Romania boiled spring water to extract salts; a salt works in China dates to approximately the same period. Salt was prized by the ancient Hebrews, Greeks, Romans, Byzantines, Hittites, Egyptians, and Indians. Salt became an impor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Flora
Flora (: floras or florae) is all the plant life present in a particular region or time, generally the naturally occurring (indigenous (ecology), indigenous) native plant, native plants. The corresponding term for animals is ''fauna'', and for fungi, it is ''funga''. Sometimes bacteria and fungi are also referred to as flora as in the terms ''gut flora'' or ''skin flora'' for purposes of specificity. Etymology The word "flora" comes from the Latin name of Flora (mythology), Flora, the goddess of plants, flowers, and fertility in Roman mythology. The technical term "flora" is then derived from a metonymy of this goddess at the end of the sixteenth century. It was first used in poetry to denote the natural vegetation of an area, but soon also assumed the meaning of a work cataloguing such vegetation. Moreover, "Flora" was used to refer to the flowers of an artificial garden in the seventeenth century. The distinction between vegetation (the general appearance of a community) and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Turing Instability
Alan Mathison Turing (; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer science, providing a formalisation of the concepts of algorithm and computation with the Turing machine, which can be considered a model of a general-purpose computer. Turing is widely considered to be the father of theoretical computer science. Born in London, Turing was raised in southern England. He graduated from King's College, Cambridge, and in 1938, earned a doctorate degree from Princeton University. During World War II, Turing worked for the Government Code and Cypher School at Bletchley Park, Britain's codebreaking centre that produced Ultra intelligence. He led Hut 8, the section responsible for German naval cryptanalysis. Turing devised techniques for speeding the breaking of German ciphers, including improvements to the pre-w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diffusive–thermal Instability
Diffusive–thermal instability or thermo–diffusive instability is an intrinsic flame instability that occurs both in premixed flames and in diffusion flames and arises because of the difference in the diffusion coefficient values for the fuel and heat transport, characterized by non-unity values of Lewis numbers. The instability mechanism that arises here is the same as in Turing instability explaining chemical morphogenesis, although the mechanism was first discovered in the context of combustion by Yakov Zeldovich in 1944 to explain the cellular structures appearing in lean hydrogen flames. Quantitative stability theory for premixed flames were developed by Gregory Sivashinsky (1977), Guy Joulin and Paul Clavin (1979) and for diffusion flames by Jong S. Kim and Forman A. Williams (1996,1997). Dispersion relation for premixed flames To neglect the influences by hydrodynamic instabilities such as Darrieus–Landau instability, Rayleigh–Taylor instability etc., the analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Schmidt Number
In fluid dynamics, the Schmidt number (denoted ) of a fluid is a dimensionless number defined as the ratio of momentum diffusivity (kinematic viscosity) and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975). The Schmidt number is the ratio of the shear component for diffusivity (viscosity divided by density) to the diffusivity for mass transfer . It physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer. It is defined as: :\mathrm = \frac = \frac = \frac = \frac where (in SI units): * \nu = \tfrac \mu \rho is the kinematic viscosity (m2/s) * is the mass diffusivity (m2/s). * is the dynamic viscosity of the fluid (Pa·s = N·s/m2 = kg/m·s) * is the density of the fluid (kg/m3) * is the Peclet Number * is the Reynolds Number. The heat transfer analog of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Metallurgy
Metallurgy is a domain of materials science and engineering that studies the physical and chemical behavior of metallic elements, their inter-metallic compounds, and their mixtures, which are known as alloys. Metallurgy encompasses both the science and the technology of metals, including the production of metals and the engineering of metal components used in products for both consumers and manufacturers. Metallurgy is distinct from the craft of metalworking. Metalworking relies on metallurgy in a similar manner to how medicine relies on medical science for technical advancement. A specialist practitioner of metallurgy is known as a metallurgist. The science of metallurgy is further subdivided into two broad categories: chemical metallurgy and physical metallurgy. Chemical metallurgy is chiefly concerned with the reduction and oxidation of metals, and the chemical performance of metals. Subjects of study in chemical metallurgy include mineral processing, the extraction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Astrophysics
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline, James Keeler, said, astrophysics "seeks to ascertain the nature of the heavenly bodies, rather than their positions or motions in space—''what'' they are, rather than ''where'' they are", which is studied in celestial mechanics. Among the subjects studied are the Sun ( solar physics), other stars, galaxies, extrasolar planets, the interstellar medium, and the cosmic microwave background. Emissions from these objects are examined across all parts of the electromagnetic spectrum, and the properties examined include luminosity, density, temperature, and chemical composition. Because astrophysics is a very broad subject, ''astrophysicists'' apply concepts and methods from many disciplines of physics, including classical mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geology
Geology (). is a branch of natural science concerned with the Earth and other astronomical objects, the rocks of which they are composed, and the processes by which they change over time. Modern geology significantly overlaps all other Earth sciences, including hydrology. It is integrated with Earth system science and planetary science. Geology describes the structure of the Earth on and beneath its surface and the processes that have shaped that structure. Geologists study the mineralogical composition of rocks in order to get insight into their history of formation. Geology determines the relative ages of rocks found at a given location; geochemistry (a branch of geology) determines their absolute ages. By combining various petrological, crystallographic, and paleontological tools, geologists are able to chronicle the geological history of the Earth as a whole. One aspect is to demonstrate the age of the Earth. Geology provides evidence for plate tectonics, the ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lewis Number
In fluid dynamics and thermodynamics, the Lewis number (denoted ) is a dimensionless number defined as the ratio of thermal diffusivity to mass diffusivity. It is used to characterize fluid flows where there is simultaneous heat and mass transfer. The Lewis number puts the thickness of the thermal boundary layer in relation to the concentration boundary layer. The Lewis number is defined as :\mathrm = \frac = \frac . where: * is the thermal diffusivity, * is the mass diffusivity, * is the thermal conductivity, * is the density, * is the mixture-averaged diffusion coefficient, * is the specific heat capacity at constant pressure. In the field of fluid mechanics, many sources define the Lewis number to be the inverse of the above definition. The Lewis number can also be expressed in terms of the Prandtl number () and the Schmidt number (): :\mathrm = \frac It is named after Warren K. Lewis (1882–1975), who was the first head of the Chemical Engineering Department at MIT. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Prandtl Number
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as:where: * \nu : momentum diffusivity ( kinematic viscosity), \nu = \mu/\rho, ( SI units: m2/s) * \alpha : thermal diffusivity, \alpha = k/(\rho c_p), (SI units: m2/s) * \mu : dynamic viscosity, (SI units: Pa s = N s/m2) * k : thermal conductivity, (SI units: W/(m·K)) * c_p : specific heat, (SI units: J/(kg·K)) * \rho : density, (SI units: kg/m3). Note that whereas the Reynolds number and Grashof number are subscripted with a scale variable, the Prandtl number contains no such length scale and is dependent only on the fluid and the fluid state. The Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity. The mass transfer analog of the Prandtl number is the Schmidt number and the ratio of the Pran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rayleigh Number
In fluid mechanics, the Rayleigh number (, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108. The Rayleigh number is defined as the product of the Grashof number (), which describes the relationship between buoyancy and viscosity within a fluid, and the Prandtl number (), which describes the relationship between momentum diffusivity and thermal diffusivity: . Hence it may also be viewed as the ratio of buoyancy and viscosity forces multiplied by the ratio of momentum and thermal diffusivities: . It is closely related to the Nusselt number (). D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
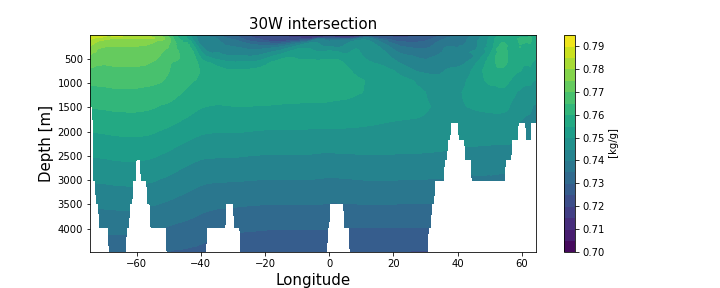
Haline Contraction Coefficient
The Haline contraction coefficient, abbreviated as β, is a coefficient that describes the change in ocean density due to a salinity change, while the potential temperature and the pressure are kept constant. It is a parameter in the Equation of state, Equation Of State (EOS) of the ocean. β is also described as the saline contraction coefficient and is measured in [kg]/[g] in the EOS that describes the ocean. An example is TEOS-10. This is the thermodynamic equation of state. β is the salinity variant of the thermal expansion coefficient α, where the density changes due to a change in temperature instead of salinity. With these two coefficients, the density ratio can be calculated. This determines the contribution of the temperature and salinity to the density of a water parcel. β is called a contraction coefficient, because when salinity increases, water becomes denser, and if the temperature increases, water becomes less dense. Definition Τhe haline contraction coeff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |