|
Diffusion Map
Diffusion maps is a dimensionality reduction or feature extraction algorithm introduced by Coifman and Lafon which computes a family of embeddings of a data set into Euclidean space (often low-dimensional) whose coordinates can be computed from the eigenvectors and eigenvalues of a diffusion operator on the data. The Euclidean distance between points in the embedded space is equal to the "diffusion distance" between probability distributions centered at those points. Different from linear dimensionality reduction methods such as principal component analysis (PCA), diffusion maps is part of the family of nonlinear dimensionality reduction methods which focus on discovering the underlying manifold that the data has been sampled from. By integrating local similarities at different scales, diffusion maps give a global description of the data-set. Compared with other methods, the diffusion map algorithm is robust to noise perturbation and computationally inexpensive. Definition of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Map Of A Torodial Helix
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (Molecular diffusion, particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure Space
A measure space is a basic object of measure theory, a branch of mathematics that studies generalized notions of volumes. It contains an underlying set, the subsets of this set that are feasible for measuring (the -algebra) and the method that is used for measuring (the measure). One important example of a measure space is a probability space. A measurable space consists of the first two components without a specific measure. Definition A measure space is a triple (X, \mathcal A, \mu), where * X is a set * \mathcal A is a -algebra on the set X * \mu is a measure on (X, \mathcal) In other words, a measure space consists of a measurable space (X, \mathcal) together with a measure on it. Example Set X = \. The \sigma-algebra on finite sets such as the one above is usually the power set, which is the set of all subsets (of a given set) and is denoted by \wp(\cdot). Sticking with this convention, we set \mathcal = \wp(X) In this simple case, the power set can be written down ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dimensionality Reduction
Nonlinear dimensionality reduction, also known as manifold learning, refers to various related techniques that aim to project high-dimensional data onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping (either from the high-dimensional space to the low-dimensional embedding or vice versa) itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis. Applications of NLDR Consider a dataset represented as a matrix (or a database table), such that each row represents a set of attributes (or features or dimensions) that describe a particular instance of something. If the number of attributes is large, then the space of unique possible rows is exponentially large. Thus, the larger the dimensionality, the more difficult it becomes to sample the space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Networks
Complex Networks is an American media and entertainment company for youth culture, based in New York City. It was founded as a bi-monthly magazine, ''Complex'', by fashion designer Marc (Ecko) Milecofsky. Complex Networks reports on popular and emerging trends in style, sneakers, food, music, sports and pop culture. Complex Networks reached over 90 million unique users per month in 2013 across its owned and operated and partner sites, socials and YouTube channels. The print magazine ceased publication with the December 2016/January 2017 issue. Complex currently has 4.55 million subscribers and 1.3 billion total views on YouTube. As of 2019, the company's yearly revenue was estimated to be US$200 million, 15% of which came from commerce. Complex Networks has been named by ''Business Insider'' as one of the Most Valuable Startups in New York, and Most Valuable Private Companies in the World. Complex Networks CEO Rich Antoniello was named among the Silicon Alley 100. In 2012, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
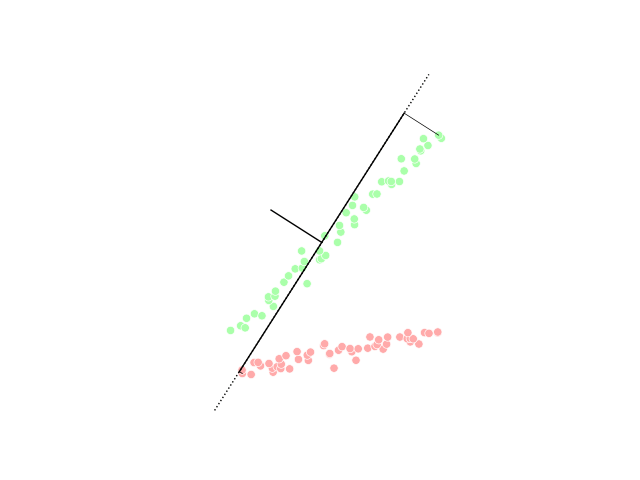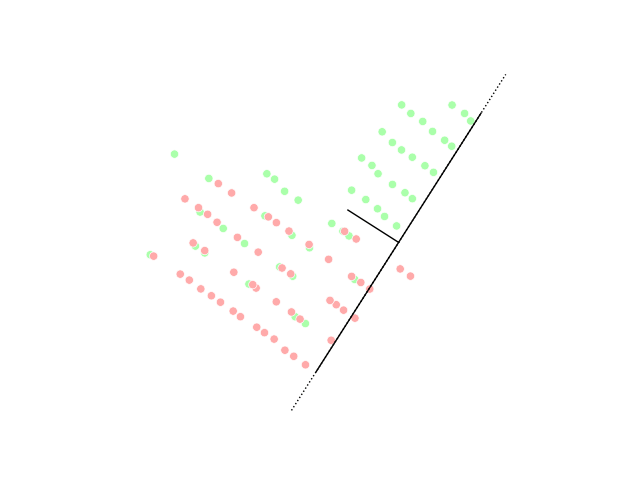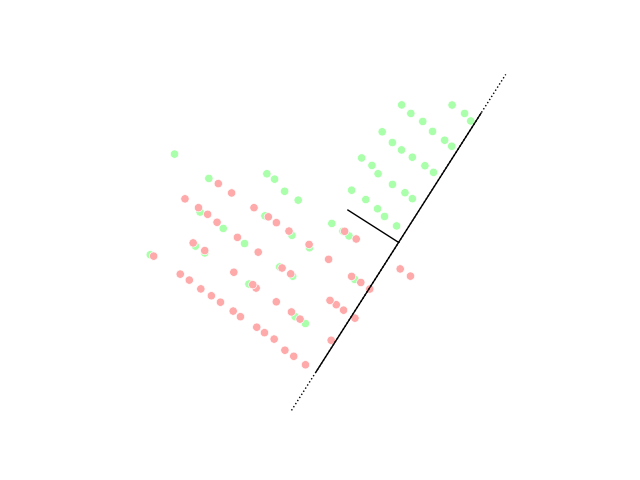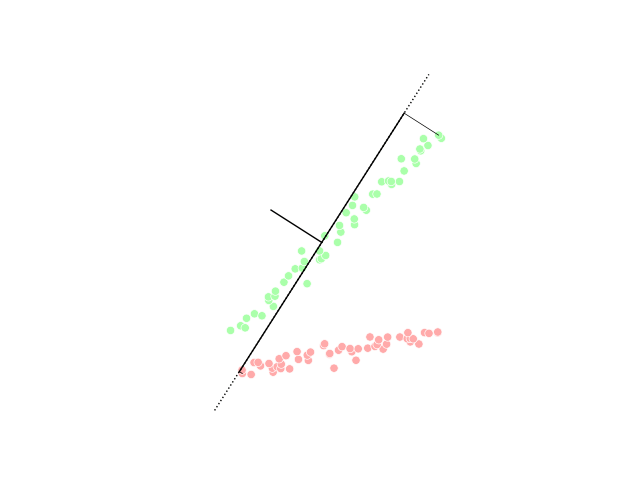
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the Spectrum of a matrix, spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard Cluster analysis, clustering method (there are many such methods, ''k''-means is discussed #Relationship with k-means, below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Facial Recognition System
A facial recognition system is a technology capable of matching a human face from a digital image or a video frame against a database of faces. Such a system is typically employed to authenticate users through ID verification services, and works by pinpointing and measuring facial features from a given image. Development began on similar systems in the 1960s, beginning as a form of computer application. Since their inception, facial recognition systems have seen wider uses in recent times on smartphones and in other forms of technology, such as robotics. Because computerized facial recognition involves the measurement of a human's physiological characteristics, facial recognition systems are categorized as biometrics. Although the accuracy of facial recognition systems as a biometric technology is lower than iris recognition and fingerprint recognition, it is widely adopted due to its contactless process. Facial recognition systems have been deployed in advanced human–compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace–Beltrami Operator
In differential geometry, the Laplace–Beltrami operator is a generalization of the Laplace operator to functions defined on submanifolds in Euclidean space and, even more generally, on Riemannian and pseudo-Riemannian manifolds. It is named after Pierre-Simon Laplace and Eugenio Beltrami. For any twice-differentiable real-valued function ''f'' defined on Euclidean space R''n'', the Laplace operator (also known as the ''Laplacian'') takes ''f'' to the divergence of its gradient vector field, which is the sum of the ''n'' pure second derivatives of ''f'' with respect to each vector of an orthonormal basis for R''n''. Like the Laplacian, the Laplace–Beltrami operator is defined as the divergence of the gradient, and is a linear operator taking functions into functions. The operator can be extended to operate on tensors as the divergence of the covariant derivative. Alternatively, the operator can be generalized to operate on differential forms using the divergence and exterio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single schem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplacian Matrix
In the mathematical field of graph theory, the Laplacian matrix, also called the graph Laplacian, admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. Named after Pierre-Simon Laplace, the graph Laplacian matrix can be viewed as a matrix form of the negative discrete Laplace operator on a graph approximating the negative continuous Laplacian obtained by the finite difference method. The Laplacian matrix relates to many useful properties of a graph. Together with Kirchhoff's theorem, it can be used to calculate the number of spanning trees for a given graph. The sparsest cut of a graph can be approximated through the Fiedler vector — the eigenvector corresponding to the second smallest eigenvalue of the graph Laplacian — as established by Cheeger's inequality. The spectral decomposition of the Laplacian matrix allows constructing low dimensional embeddings that appear in many machine learning applications and determines a spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Kernel
In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in the original function space. The transformed function can generally be mapped back to the original function space using the ''inverse transform''. General form An integral transform is any transform ''T'' of the following form: :(Tf)(u) = \int_^ f(t)\, K(t, u)\, dt The input of this transform is a function ''f'', and the output is another function ''Tf''. An integral transform is a particular kind of mathematical operator. There are numerous useful integral transforms. Each is specified by a choice of the function K of two variables, the kernel function, integral kernel or nucleus of the transform. Some kernels have an associated ''inverse kernel'' K^( u,t ) which (roughly speaking) yields an inverse transform: :f(t) = \int_^ (Tf)(u) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionality Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable (hard to control or deal with). Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Approaches can also be divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermediat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |