|
Desmos Pannosus
Desmos is an advanced graphing calculator implemented as a web application and a mobile application written in JavaScript. History It was founded by Eli Luberoff, a math and physics double major from Yale University, and was launched as a startup at TechCrunch's Disrupt New York conference in 2011. , it had received around 1 million US dollars of funding from Kapor Capital, Learn Capital, Kindler Capital, Elm Street Ventures and Google Ventures. In May 2022, Amplify acquired the Desmos curriculum and teacher.desmos.com. Some 50 employees joined Amplify. Desmos Studio was spun off as a separate public benefit corporation focused on building calculator products and other math tools. The name ''Desmos'' came from the Greek word which means a bond or a tie. Features In addition to graphing both equations and inequalities, it also features lists, plots, regressions, interactive variables, graph restriction, simultaneous graphing, piece wise function graphing, po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphing Calculator
A graphing calculator (also graphics calculator or graphic display calculator) is a handheld computer that is capable of plotting graphs, solving simultaneous equations, and performing other tasks with variables. Most popular graphing calculators are programmable calculators, allowing the user to create customized programs, typically for scientific, engineering or education applications. They have large screens that display several lines of text and calculations. History An early graphing calculator was designed in 1921 by electrical engineer Edith Clarke. The calculator was used to solve problems with electrical power line transmission. Casio produced the first commercially available graphing calculator in 1985. Sharp produced its first graphing calculator in 1986. Hewlett Packard followed in 1988. Texas Instruments in 1990. Features Computer algebra systems Some graphing calculators have a computer algebra system (CAS), which means that they are capable of p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Programmable Calculator
Programmable calculators are calculators that can automatically carry out a sequence of operations under control of a stored program. Most are Turing complete, and, as such, are theoretically general-purpose computers. However, their user interfaces and programming environments are specifically tailored to make performing small-scale numerical computations convenient, rather than general-purpose use. The first programmable calculators such as the IBM CPC used punched cards or other media for program storage. Hand-held electronic calculators store programs on magnetic strips, removable read-only memory cartridges, flash memory, or in battery-backed read/write memory. Since the early 1990s, most of these flexible handheld units belong to the class of graphing calculators. Before the mass-manufacture of inexpensive dot-matrix LCDs, however, programmable calculators usually featured a one-line numeric or alphanumeric display. The Big Four manufacturers of programmable calcula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetris
''Tetris'' (russian: link=no, Тетрис) is a puzzle video game created by Soviet Union, Soviet software engineer Alexey Pajitnov in 1984. It has been published by several companies for multiple platforms, most prominently during a dispute over the appropriation of the rights in the late 1980s. After a significant period of publication by Nintendo, the rights reverted to Pajitnov in 1996, who co-founded the Tetris Company with Henk Rogers to manage licensing. In ''Tetris'', players complete lines by moving differently shaped pieces (tetrominoes), which descend onto the playing field. The completed lines disappear and grant the player points, and the player can proceed to fill the vacated spaces. The game ends when the uncleared lines reach the top of the playing field. The longer the player can delay this outcome, the higher their score will be. In multiplayer games, players must last longer than their opponents; in certain versions, players can inflict penalties on opponents ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mandelbrot Set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value. This set was first defined and drawn by Robert W. Brooks and Peter Matelski in 1978, as part of a study of Kleinian groups. Afterwards, in 1980, Benoit Mandelbrot obtained high-quality visualizations of the set while working at IBM's Thomas J. Watson Research Center in Yorktown Heights, New York. Images of the Mandelbrot set exhibit an elaborate and infinitely complicated boundary that reveals progressively ever-finer recursive detail at increasing magnifications; mathematically, one would say that the boundary of the Mandelbrot set is a ''fractal curve''. The "style" of this recursive detail depends on the region of the set boundary being examined. Mandelbrot set images may be created by sampling the complex numbers and testing, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Functions
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions). History Complex analysis is one of the classical branches in mathematics, with roots in the 18th century and just prior. Important mathematicians associated with complex numbers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
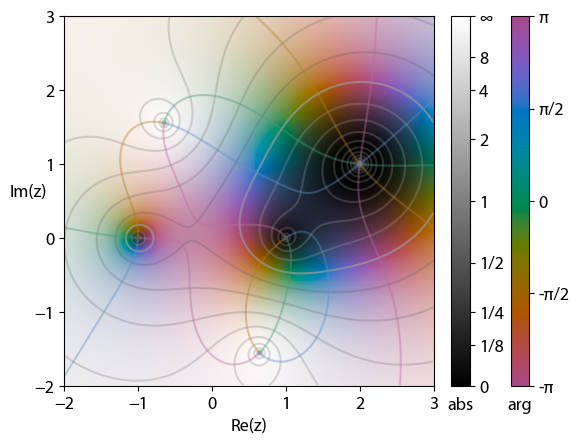
Domain Coloring
In complex analysis, domain coloring or a color wheel graph is a technique for visualizing complex functions by assigning a color to each point of the complex plane. By assigning points on the complex plane to different colors and brightness, domain coloring allows for a function from the complex plane to itself — whose graph would normally require four space dimensions — to be easily represented and understood. This provides insight to the fluidity of complex functions and shows natural geometric extensions of real functions. Motivation A graph of a real function can be drawn in two dimensions because there are two represented variables, x and y. However, complex numbers are represented by two variables and therefore two dimensions; this means that representing a complex function (more precisely, a complex-valued function of one complex variable f: \mathbb \to \mathbb) requires the visualization of four dimensions. One way to achieve that is with a Riemann surface, but anoth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-dimensional Space
In mathematics, a plane is a Euclidean ( flat), two-dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional Euclidean geometry. Sometimes the word ''plane'' is used more generally to describe a two-dimensional surface, for example the hyperbolic plane and elliptic plane. When working exclusively in two-dimensional Euclidean space, the definite article is used, so ''the'' plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Euclidean geometry Euclid set forth the first great landmark of mathematical thought, an axio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequality (mathematics)
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities: * The notation ''a'' ''b'' means that ''a'' is greater than ''b''. In either case, ''a'' is not equal to ''b''. These relations are known as strict inequalities, meaning that ''a'' is strictly less than or strictly greater than ''b''. Equivalence is excluded. In contrast to strict inequalities, there are two types of inequality relations that are not strict: * The notation ''a'' ≤ ''b'' or ''a'' ⩽ ''b'' means that ''a'' is less than or equal to ''b'' (or, equivalently, at most ''b'', or not greater than ''b''). * The notation ''a'' ≥ ''b'' or ''a'' ⩾ ''b'' means that ''a'' is greater than or equal to ''b'' (or, equivalently, at least ''b'', or not less than ''b''). The r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permalink
A permalink or permanent link is a URL that is intended to remain unchanged for many years into the future, yielding a hyperlink that is less susceptible to link rot. Permalinks are often rendered simply, that is, as clean URLs, to be easier to type and remember. Most modern blogging and content-syndication software systems support such links. Sometimes URL shortening is used to create them. A permalink is a type of persistent identifier and the word ''permalink'' is sometimes used as a synonym of ''persistent identifier.'' More often, though, ''permalink'' is applied to persistent identifiers which are generated by a content management system for pages served by that system. This usage is especially common in the blogosphere. Such links are not maintained by an outside authority, and their persistence is dependent on the durability of the content management system itself. History In the early years of the web, all content was static, and thus all hyperlinks pointed at a filen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book '' Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a complex function of a complex variable defined as: :\operatorname z = \frac\int_0^z e^\,\mathrm dt. This integral is a special (non- elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real. In statistics, for non-negative values of , the error function has the following interpretation: for a random variable that is normally distributed with mean 0 and standard deviation , is the probability that falls in the range . Two closely related functions are the complementary error function () defined as :\operatorname z = 1 - \operatorname z, and the imaginary error function () defined as :\operatorname z = -i\operatorname iz, where is the imaginary unit Name The name "error functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |