|
Cosine Similarity
In data analysis, cosine similarity is a measure of similarity between two sequences of numbers. For defining it, the sequences are viewed as vectors in an inner product space, and the cosine similarity is defined as the cosine of the angle between them, that is, the dot product of the vectors divided by the product of their lengths. It follows that the cosine similarity does not depend on the magnitudes of the vectors, but only on their angle. The cosine similarity always belongs to the interval 1, 1 For example, two proportional vectors have a cosine similarity of 1, two orthogonal vectors have a similarity of 0, and two opposite vectors have a similarity of -1. The cosine similarity is particularly used in positive space, where the outcome is neatly bounded in ,1/math>. For example, in information retrieval and text mining, each word is assigned a different coordinate and a document is represented by the vector of the numbers of occurrences of each word in the document. C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Analysis
Data analysis is a process of inspecting, cleansing, transforming, and modeling data with the goal of discovering useful information, informing conclusions, and supporting decision-making. Data analysis has multiple facets and approaches, encompassing diverse techniques under a variety of names, and is used in different business, science, and social science domains. In today's business world, data analysis plays a role in making decisions more scientific and helping businesses operate more effectively. Data mining is a particular data analysis technique that focuses on statistical modeling and knowledge discovery for predictive rather than purely descriptive purposes, while business intelligence covers data analysis that relies heavily on aggregation, focusing mainly on business information. In statistical applications, data analysis can be divided into descriptive statistics, exploratory data analysis (EDA), and confirmatory data analysis (CDA). EDA focuses on discovering ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnitude (mathematics)
In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an ordering (or ranking)—of the class of objects to which it belongs. In physics, magnitude can be defined as quantity or distance. History The Greeks distinguished between several types of magnitude, including: *Positive fractions *Line segments (ordered by length) * Plane figures (ordered by area) * Solids (ordered by volume) * Angles (ordered by angular magnitude) They proved that the first two could not be the same, or even isomorphic systems of magnitude. They did not consider negative magnitudes to be meaningful, and ''magnitude'' is still primarily used in contexts in which zero is either the smallest size or less than all possible sizes. Numbers The magnitude of any number x is usually called its ''absolute value'' or ''modulus'', de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
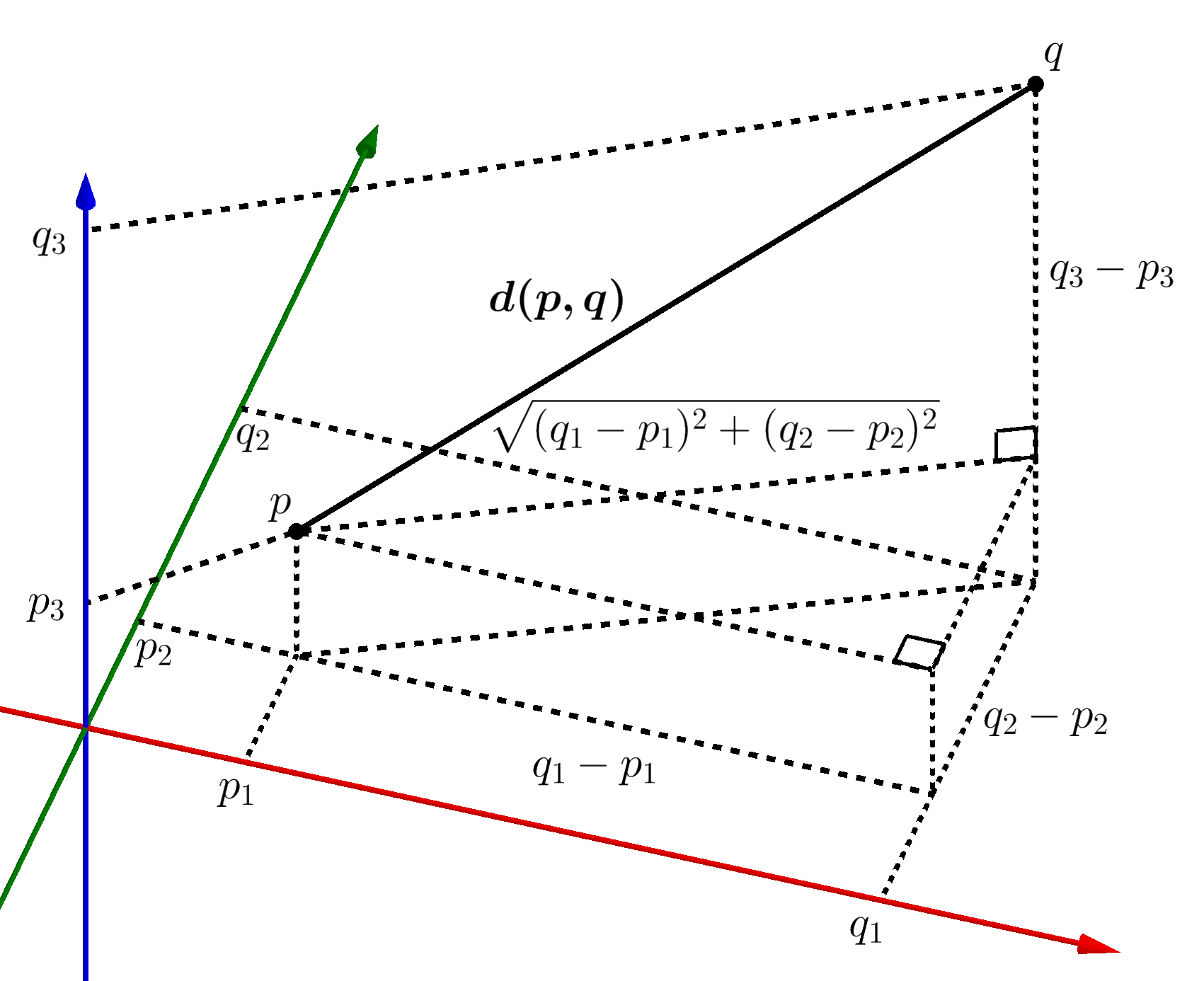
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications in statistic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norm (mathematics)
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance of a vector from the origin is a norm, called the Euclidean norm, or 2-norm, which may also be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm, but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meanings. It may be a synonym of "seminorm". A pseudonorm may satisfy the same axioms as a norm, with the equality replaced by an inequality "\,\leq\," in the homogeneity axiom. It can als ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squared Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two Point (geometry), points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine Similarity
In data analysis, cosine similarity is a measure of similarity between two sequences of numbers. For defining it, the sequences are viewed as vectors in an inner product space, and the cosine similarity is defined as the cosine of the angle between them, that is, the dot product of the vectors divided by the product of their lengths. It follows that the cosine similarity does not depend on the magnitudes of the vectors, but only on their angle. The cosine similarity always belongs to the interval 1, 1 For example, two proportional vectors have a cosine similarity of 1, two orthogonal vectors have a similarity of 0, and two opposite vectors have a similarity of -1. The cosine similarity is particularly used in positive space, where the outcome is neatly bounded in ,1/math>. For example, in information retrieval and text mining, each word is assigned a different coordinate and a document is represented by the vector of the numbers of occurrences of each word in the document. C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarz Inequality
Schwarz may refer to: * Schwarz, Germany, a municipality in Mecklenburg-Vorpommern, Germany * Schwarz (surname), a surname (and list of people with the surname) * Schwarz (musician), American DJ and producer * ''Schwarz'' (Böhse Onkelz album), released simultaneously with ''Weiß'', 1993 * ''Schwarz'' (Conrad Schnitzler album), a reissue of the 1971 Kluster album ''Eruption'' * Schwarz (cards), in some card games, a Schneider (low point score) in which no tricks are taken * Schwarz Gruppe, a multinational retail group * Schwarz Pharma, a German drug company See also * * * Schwartz (other) Schwartz may refer to: * Schwartz (surname), a surname (and list of people with the name) * Schwartz (brand), a spice brand *Schwartz's, a delicatessen in Montreal, Quebec, Canada * Schwartz Publishing, an Australian publishing house *"Danny Schwar ... * Schwarzhorn (other) * Swartz (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If , , and are the lengths of the sides of the triangle, with no side being greater than , then the triangle inequality states that :z \leq x + y , with equality only in the degenerate case of a triangle with zero area. In Euclidean geometry and some other geometries, the triangle inequality is a theorem about distances, and it is written using vectors and vector lengths ( norms): :\, \mathbf x + \mathbf y\, \leq \, \mathbf x\, + \, \mathbf y\, , where the length of the third side has been replaced by the vector sum . When and are real numbers, they can be viewed as vectors in , and the trian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distance Metric
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson's ''r'', the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation, or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normalization (statistics)
In statistics and applications of statistics, normalization can have a range of meanings. In the simplest cases, normalization of ratings means adjusting values measured on different scales to a notionally common scale, often prior to averaging. In more complicated cases, normalization may refer to more sophisticated adjustments where the intention is to bring the entire probability distributions of adjusted values into alignment. In the case of normalization of scores in educational assessment, there may be an intention to align distributions to a normal distribution. A different approach to normalization of probability distributions is quantile normalization, where the quantiles of the different measures are brought into alignment. In another usage in statistics, normalization refers to the creation of shifted and scaled versions of statistics, where the intention is that these normalized values allow the comparison of corresponding normalized values for different datasets in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
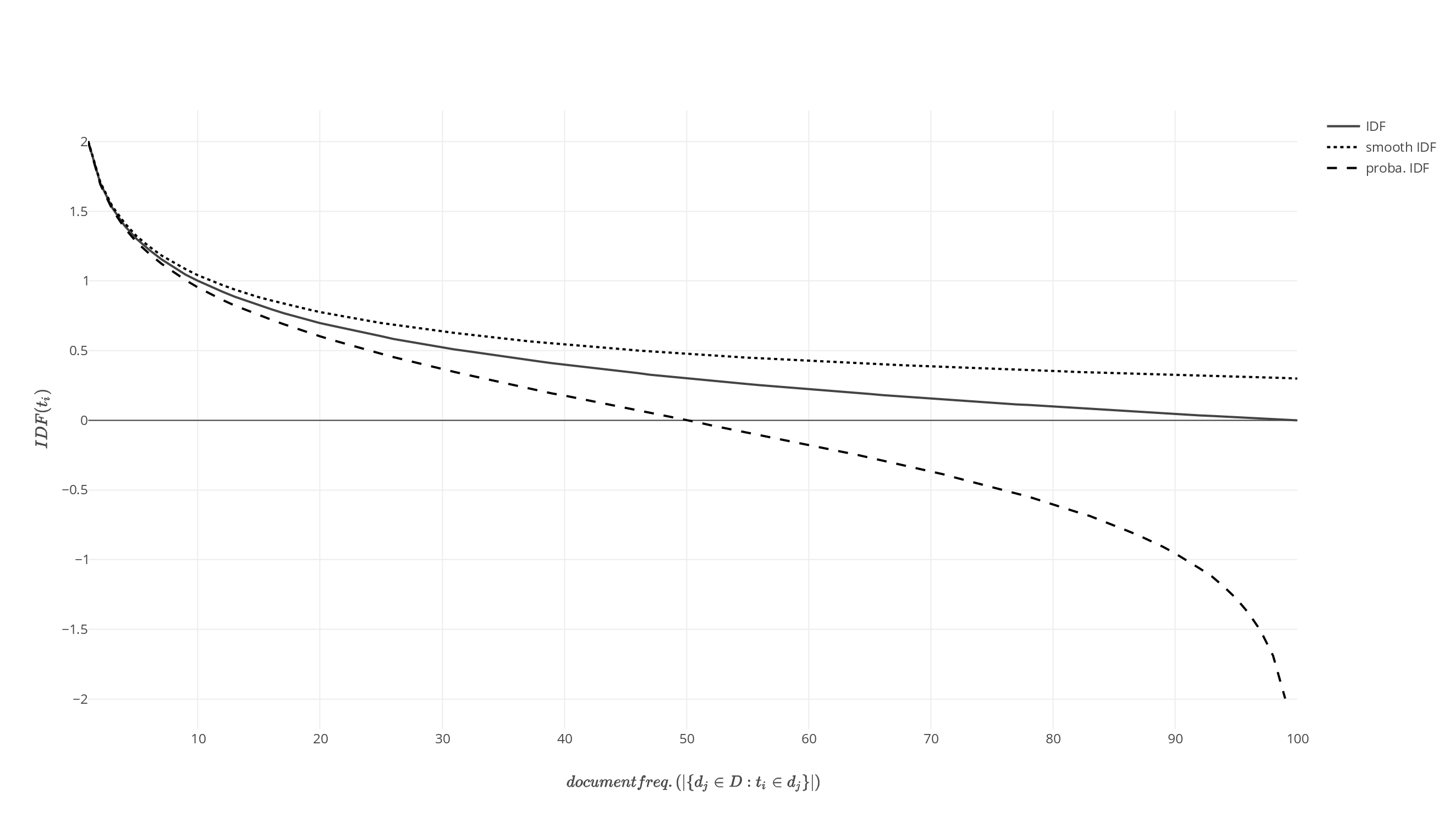
Tf–idf
In information retrieval, tf–idf (also TF*IDF, TFIDF, TF–IDF, or Tf–idf), short for term frequency–inverse document frequency, is a numerical statistic that is intended to reflect how important a word is to a document in a collection or corpus. It is often used as a weighting factor in searches of information retrieval, text mining, and user modeling. The tf–idf value increases proportionally to the number of times a word appears in the document and is offset by the number of documents in the corpus that contain the word, which helps to adjust for the fact that some words appear more frequently in general. tf–idf is one of the most popular term-weighting schemes today. A survey conducted in 2015 showed that 83% of text-based recommender systems in digital libraries use tf–idf. Variations of the tf–idf weighting scheme are often used by search engines as a central tool in scoring and ranking a document's relevance given a user query. tf–idf can be successfully ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
