squared Euclidean distance on:
[Wikipedia]
[Google]
[Amazon]
 In
In
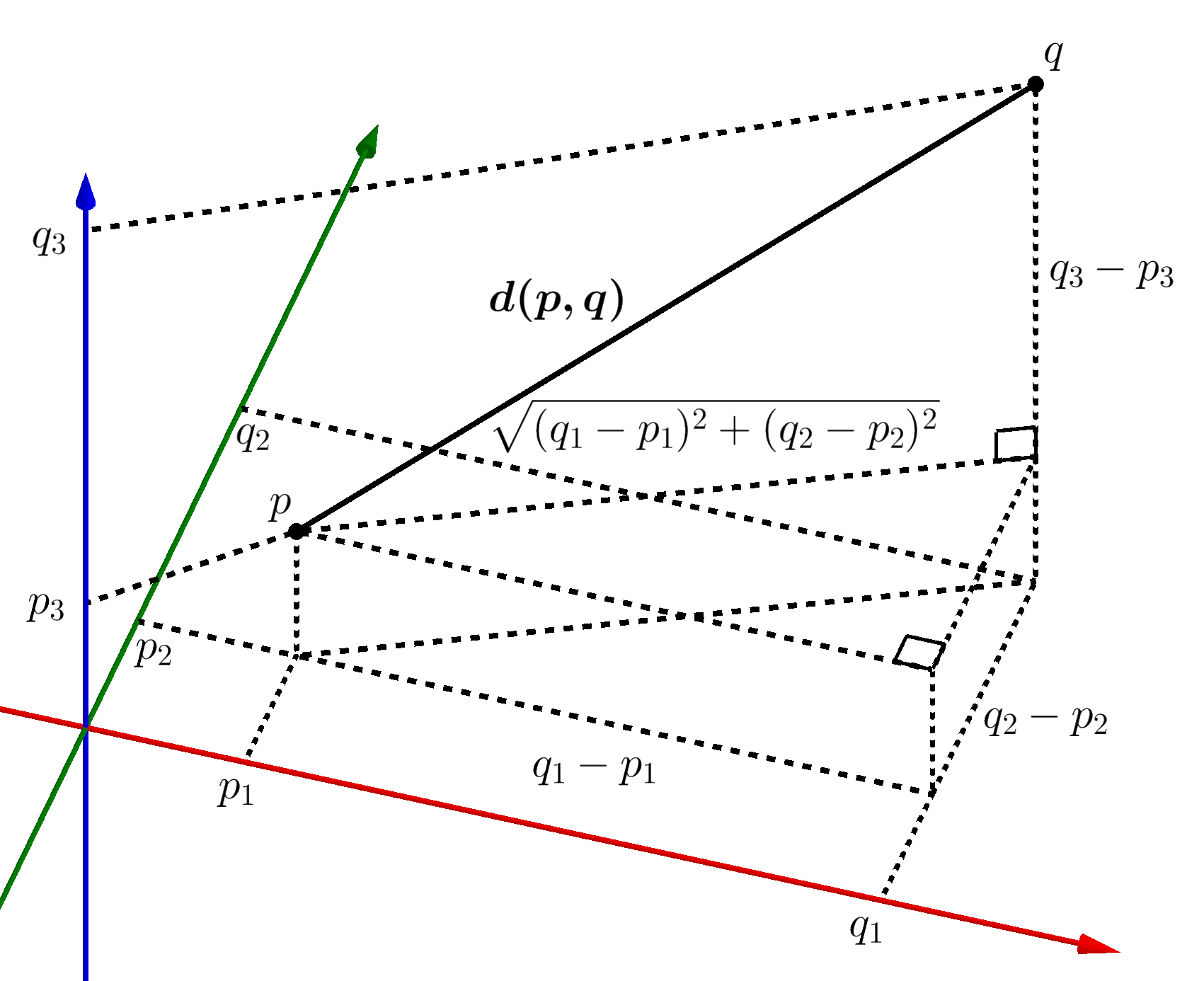 In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the Euclidean distance between two points in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics ther ...
is the length
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the Interna ...
of a line segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between ...
between the two points.
It can be calculated from the Cartesian coordinate
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in ...
s of the points using the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
and Pythagoras
Pythagoras of Samos ( grc, Πυθαγόρας ὁ Σάμιος, Pythagóras ho Sámios, Pythagoras the Samos, Samian, or simply ; in Ionian Greek; ) was an ancient Ionians, Ionian Ancient Greek philosophy, Greek philosopher and the eponymou ...
, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century.
The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line In Euclidean geometry, the distance from a point to a line'' is the shortest distance from a given point to any point on an infinite straight line. It is the perpendicular distance of the point to the line, the length of the line segment which join ...
. In advanced mathematics, the concept of distance has been generalized to abstract metric space
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general settin ...
s, and other distances than Euclidean have been studied. In some applications in statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of ...
and optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
, the square of the Euclidean distance is used instead of the distance itself.
Distance formulas
One dimension
The distance between any two points on thereal line
In elementary mathematics, a number line is a picture of a graduated straight line (geometry), line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real ...
is the absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), an ...
of the numerical difference of their coordinates, their absolute difference
The absolute difference of two real numbers x and y is given by , x-y, , the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y. It is a special case of the Lp distance for a ...
. Thus if and are two points on the real line, then the distance between them is given by:
A more complicated formula, giving the same value, but generalizing more readily to higher dimensions, is:
In this formula, squaring and then taking the square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
E ...
leaves any positive number unchanged, but replaces any negative number by its absolute value.
Two dimensions
In theEuclidean plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions of ...
, let point have Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
and let point have coordinates . Then the distance between and is given by:
This can be seen by applying the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
to a right triangle
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right an ...
with horizontal and vertical sides, having the line segment from to as its hypotenuse. The two squared formulas inside the square root give the areas of squares on the horizontal and vertical sides, and the outer square root converts the area of the square on the hypotenuse into the length of the hypotenuse.
It is also possible to compute the distance for points given by polar coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the or ...
. If the polar coordinates of are and the polar coordinates of are , then their distance is given by the law of cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states ...
:
When and are expressed as complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
s in the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the ...
, the same formula for one-dimensional points expressed as real numbers can be used, although here the absolute value sign indicates the complex norm
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is ze ...
:
Higher dimensions
 In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is
Objects other than points
For pairs of objects that are not both points, the distance can most simply be defined as the smallest distance between any two points from the two objects, although more complicated generalizations from points to sets such asHausdorff distance In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric ...
are also commonly used. Formulas for computing distances between different types of objects include:
*The distance from a point to a line In Euclidean geometry, the distance from a point to a line'' is the shortest distance from a given point to any point on an infinite straight line. It is the perpendicular distance of the point to the line, the length of the line segment which join ...
, in the Euclidean plane
*The distance from a point to a plane In Euclidean space, the distance from a point to a plane is the distance between a given point and its orthogonal projection on the plane, the perpendicular distance to the nearest point on the plane.
It can be found starting with a change of varia ...
in three-dimensional Euclidean space
*The distance between two lines
The distance between two parallel lines in the plane is the minimum distance between any two points.
Formula and proof
Because the lines are parallel, the perpendicular distance between them is a constant, so it does not matter which point is ...
in three-dimensional Euclidean space
Properties
The Euclidean distance is the prototypical example of the distance in ametric space
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general settin ...
, and obeys all the defining properties of a metric space:
*It is ''symmetric'', meaning that for all points and , . That is (unlike road distance with one-way streets) the distance between two points does not depend on which of the two points is the start and which is the destination.
*It is ''positive'', meaning that the distance between every two distinct points is a positive number
In mathematics, the sign of a real number is its property of being either positive, negative, or zero. Depending on local conventions, zero may be considered as being neither positive nor negative (having no sign or a unique third sign), or it ...
, while the distance from any point to itself is zero.
*It obeys the triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.
This statement permits the inclusion of degenerate triangles, but ...
: for every three points , , and , . Intuitively, traveling from to via cannot be any shorter than traveling directly from to .
Another property, Ptolemy's inequality
In Euclidean geometry, Ptolemy's inequality relates the six distances determined by four points in the plane or in a higher-dimensional space. It states that, for any four points , , , and , the following inequality holds:
:\overline\cdot \overline ...
, concerns the Euclidean distances among four points , , , and . It states that
For points in the plane, this can be rephrased as stating that for every quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
, the products of opposite sides of the quadrilateral sum to at least as large a number as the product of its diagonals. However, Ptolemy's inequality applies more generally to points in Euclidean spaces of any dimension, no matter how they are arranged. For points in metric spaces that are not Euclidean spaces, this inequality may not be true. Euclidean distance geometry Distance geometry is the branch of mathematics concerned with characterizing and studying sets of points based ''only'' on given values of the distances between pairs of points. More abstractly, it is the study of semimetric spaces and the isome ...
studies properties of Euclidean distance such as Ptolemy's inequality, and their application in testing whether given sets of distances come from points in a Euclidean space.
According to the Beckman–Quarles theorem
In geometry, the Beckman–Quarles theorem, named after Frank S. Beckman and Donald A. Quarles Jr., states that if a transformation of the Euclidean plane or a higher-dimensional Euclidean space preserves unit distances, then it preserves all ...
, any transformation of the Euclidean plane or of a higher-dimensional Euclidean space that preserves unit distances must be an isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' mea ...
, preserving all distances.
Squared Euclidean distance
In many applications, and in particular when comparing distances, it may be more convenient to omit the final square root in the calculation of Euclidean distances. The value resulting from this omission is thesquare
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
of the Euclidean distance, and is called the squared Euclidean distance. As an equation, it can be expressed as a sum of squares:
Beyond its application to distance comparison, squared Euclidean distance is of central importance in statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of ...
, where it is used in the method of least squares
The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems (sets of equations in which there are more equations than unknowns) by minimizing the sum of the squares of the res ...
, a standard method of fitting statistical estimates to data by minimizing the average of the squared distances between observed and estimated values, and as the simplest form of divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the ...
to compare probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon i ...
s. The addition of squared distances to each other, as is done in least squares fitting, corresponds to an operation on (unsquared) distances called Pythagorean addition
In mathematics, Pythagorean addition is a binary operation on the real numbers that computes the length of the hypotenuse of a right triangle, given its two sides. According to the Pythagorean theorem, for a triangle with sides a and b, this le ...
. In cluster analysis
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of ...
, squared distances can be used to strengthen the effect of longer distances.
Squared Euclidean distance does not form a metric space, as it does not satisfy the triangle inequality. However it is a smooth, strictly convex function
In mathematics, a real-valued function is called convex if the line segment between any two points on the graph of a function, graph of the function lies above the graph between the two points. Equivalently, a function is convex if its epigra ...
of the two points, unlike the distance, which is non-smooth (near pairs of equal points) and convex but not strictly convex. The squared distance is thus preferred in optimization theory
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
, since it allows convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory.
Convex sets
A subset C \subseteq X of s ...
to be used. Since squaring is a monotonic function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
of non-negative values, minimizing squared distance is equivalent to minimizing the Euclidean distance, so the optimization problem is equivalent in terms of either, but easier to solve using squared distance.
The collection of all squared distances between pairs of points from a finite set may be stored in a Euclidean distance matrix In mathematics, a Euclidean distance matrix is an matrix representing the spacing of a set of points in Euclidean space.
For points x_1,x_2,\ldots,x_n in -dimensional space , the elements of their Euclidean distance matrix are given by squares ...
, and is used in this form in distance geometry.
Generalizations
In more advanced areas of mathematics, when viewing Euclidean space as avector space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called ''vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but can ...
, its distance is associated with a norm
Naturally occurring radioactive materials (NORM) and technologically enhanced naturally occurring radioactive materials (TENORM) consist of materials, usually industrial wastes or by-products enriched with radioactive elements found in the envir ...
called the Euclidean norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean s ...
, defined as the distance of each vector from the origin
Origin(s) or The Origin may refer to:
Arts, entertainment, and media
Comics and manga
* Origin (comics), ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002
* The Origin (Buffy comic), ''The Origin'' (Bu ...
. One of the important properties of this norm, relative to other norms, is that it remains unchanged under arbitrary rotations of space around the origin. By Dvoretzky's theorem In mathematics, Dvoretzky's theorem is an important structural theorem about normed vector spaces proved by Aryeh Dvoretzky in the early 1960s, answering a question of Alexander Grothendieck. In essence, it says that every sufficiently high-dimens ...
, every finite-dimensional normed vector space
In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers, on which a norm is defined. A norm is the formalization and the generalization to real vector spaces of the intuitive notion of "length" i ...
has a high-dimensional subspace on which the norm is approximately Euclidean; the Euclidean norm is the
only norm with this property. It can be extended to infinite-dimensional vector spaces as the L2 norm or L2 distance. The Euclidean distance gives Euclidean space the structure of a topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points ...
, the Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is the natural topology induced on n-dimensional Euclidean space \R^n by the Euclidean distance, Euclidean metric.
Definition
The Euclidean norm on \R^n is the non-negative f ...
, with the open ball
In mathematics, a ball is the solid figure bounded by a ''sphere''; it is also called a solid sphere. It may be a closed ball (including the boundary points that constitute the sphere) or an open ball (excluding them).
These concepts are defin ...
s (subsets of points at less than a given distance from a given point) as its neighborhoods
A neighbourhood (British English, Irish English, Australian English and Canadian English) or neighborhood (American English; American and British English spelling differences, see spelling differences) is a geographically localised community ...
.
Other common distances on Euclidean spaces and low-dimensional vector spaces include:
*Chebyshev distance
In mathematics, Chebyshev distance (or Tchebychev distance), maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension. It is na ...
, which measures distance assuming only the most significant dimension is relevant.
*Manhattan distance
A taxicab geometry or a Manhattan geometry is a geometry whose usual distance function or Metric (mathematics), metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences ...
, which measures distance following only axis-aligned directions.
*Minkowski distance
The Minkowski distance or Minkowski metric is a metric in a normed vector space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance. It is named after the German mathematician Hermann Minkowski.
...
, a generalization that unifies Euclidean distance, Manhattan distance, and Chebyshev distance.
For points on surfaces in three dimensions, the Euclidean distance should be distinguished from the geodesic
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. ...
distance, the length of a shortest curve that belongs to the surface. In particular, for measuring great-circle distances on the earth or other spherical or near-spherical surfaces, distances that have been used include the haversine distance The haversine formula determines the great-circle distance between two points on a sphere given their longitudes and latitudes. Important in navigation, it is a special case of a more general formula in spherical trigonometry, the law of haversines, ...
giving great-circle distances between two points on a sphere from their longitudes and latitudes, and Vincenty's formulae
Vincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty (1975a). They are based on the assumption that the figure of the Earth ...
also known as "Vincent distance" for distance on a spheroid.
History
Euclidean distance is the distance inEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics ther ...
; both concepts are named after ancient Greek mathematician Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
, whose ''Elements'' became a standard textbook in geometry for many centuries. Concepts of length
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the Interna ...
and distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). ...
are widespread across cultures, can be dated to the earliest surviving "protoliterate" bureaucratic documents from Sumer
Sumer () is the earliest known civilization in the historical region of southern Mesopotamia (south-central Iraq), emerging during the Chalcolithic and early Bronze Ages between the sixth and fifth millennium BC. It is one of the cradles of c ...
in the fourth millennium BC (far before Euclid), and have been hypothesized to develop in children earlier than the related concepts of speed and time. But the notion of a distance, as a number defined from two points, does not actually appear in Euclid's ''Elements''. Instead, Euclid approaches this concept implicitly, through the congruence of line segments, through the comparison of lengths of line segments, and through the concept of proportionality.
The Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
is also ancient, but it could only take its central role in the measurement of distances after the invention of Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
by René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathem ...
in 1637. The distance formula itself was first published in 1731 by Alexis Clairaut
Alexis Claude Clairaut (; 13 May 1713 – 17 May 1765) was a French mathematician, astronomer, and geophysicist. He was a prominent Newtonian whose work helped to establish the validity of the principles and results that Sir Isaac Newton had out ...
. Because of this formula, Euclidean distance is also sometimes called Pythagorean distance. Although accurate measurements of long distances on the earth's surface, which are not Euclidean, had again been studied in many cultures since ancient times (see history of geodesy
The history of geodesy deals with the historical development of measurements and representations of the Earth. The corresponding scientific discipline, '' geodesy'' ( /dʒiːˈɒdɪsi/), began in pre-scientific antiquity and blossomed during th ...
), the idea that Euclidean distance might not be the only way of measuring distances between points in mathematical spaces came even later, with the 19th-century formulation of non-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geo ...
. The definition of the Euclidean norm and Euclidean distance for geometries of more than three dimensions also first appeared in the 19th century, in the work of Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He ...
.
References
{{DEFAULTSORT:Euclidean Distance Distance Length Metric geometry Pythagorean theorem