|
Complex Conjugate Representation
In mathematics, if is a group and is a representation of it over the complex vector space , then the complex conjugate representation is defined over the complex conjugate vector space as follows: : is the conjugate of for all in . is also a representation, as one may check explicitly. If is a real Lie algebra and is a representation of it over the vector space , then the conjugate representation is defined over the conjugate vector space as follows: : is the conjugate of for all in .This is the mathematicians' convention. Physicists use a different convention where the Lie bracket of two real vectors is an imaginary vector. In the physicist's convention, insert a minus in the definition. is also a representation, as one may check explicitly. If two real Lie algebras have the same complexification, and we have a complex representation of the complexified Lie algebra, their conjugate representations are still going to be different. See spinor for some examples ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set and an Binary operation, operation that combines any two Element (mathematics), elements of the set to produce a third element of the set, in such a way that the operation is Associative property, associative, an identity element exists and every element has an Inverse element, inverse. These three axioms hold for Number#Main classification, number systems and many other mathematical structures. For example, the integers together with the addition operation form a group. The concept of a group and the axioms that define it were elaborated for handling, in a unified way, essential structural properties of very different mathematical entities such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry groups arise naturally in the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and their algebraic operations (for example, matrix addition, matrix multiplication). The theory of matrices and linear operators is well-understood, so representations of more abstract objects in terms of familiar linear algebra objects helps glean properties and sometimes simplify calculations on more abstract theories. The algebraic objects amenable to such a description include groups, associative algebras and Lie algebras. The most prominent of these (and historically the first) is the representation theory of groups, in which elements of a group are represented by invertible matrices in such a way that the group operation i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called ''vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. The terms real vector space and complex vector space are often used to specify the nature of the scalars: real coordinate space or complex coordinate space. Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugate Vector Space
In mathematics, the complex conjugate of a complex vector space V\, is a complex vector space \overline V, which has the same elements and additive group structure as V, but whose scalar multiplication involves conjugation of the scalars. In other words, the scalar multiplication of \overline V satisfies \alpha\,*\, v = where * is the scalar multiplication of \overline and \cdot is the scalar multiplication of V. The letter v stands for a vector in V, \alpha is a complex number, and \overline denotes the complex conjugate of \alpha. More concretely, the complex conjugate vector space is the same underlying vector space (same set of points, same vector addition and real scalar multiplication) with the conjugate linear complex structure J (different multiplication by i). Motivation If V and W are complex vector spaces, a function f : V \to W is antilinear if f(v + w) = f(v) + f(w) \quad \text \quad f(\alpha v) = \overline \, f(v) With the use of the conjugate vector space \overline ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Linear Map
In mathematics, the complex conjugate of a complex vector space V\, is a complex vector space \overline V, which has the same elements and additive group structure as V, but whose scalar multiplication involves conjugation of the scalars. In other words, the scalar multiplication of \overline V satisfies \alpha\,*\, v = where * is the scalar multiplication of \overline and \cdot is the scalar multiplication of V. The letter v stands for a vector in V, \alpha is a complex number, and \overline denotes the complex conjugate of \alpha. More concretely, the complex conjugate vector space is the same underlying vector space (same set of points, same vector addition and real scalar multiplication) with the conjugate linear complex structure J (different multiplication by i). Motivation If V and W are complex vector spaces, a function f : V \to W is antilinear if f(v + w) = f(v) + f(w) \quad \text \quad f(\alpha v) = \overline \, f(v) With the use of the conjugate vector space \overline ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an Binary operation, operation called the Lie bracket, an Alternating multilinear map, alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identity. The Lie bracket of two vectors x and y is denoted [x,y]. The vector space \mathfrak g together with this operation is a non-associative algebra, meaning that the Lie bracket is not necessarily associative property, associative. Lie algebras are closely related to Lie groups, which are group (mathematics), groups that are also smooth manifolds: any Lie group gives rise to a Lie algebra, which is its tangent space at the identity. Conversely, to any finite-dimensional Lie algebra over real or complex numbers, there is a corresponding connected space, connected Lie group unique up to finite coverings (Lie's third theorem). This Lie group–Lie algebra correspondence, correspondence allows one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Bracket Of Vector Fields
In the mathematical field of differential topology, the Lie bracket of vector fields, also known as the Jacobi–Lie bracket or the commutator of vector fields, is an operator that assigns to any two vector fields ''X'' and ''Y'' on a smooth manifold ''M'' a third vector field denoted . Conceptually, the Lie bracket is the derivative of ''Y'' along the flow generated by ''X'', and is sometimes denoted ''\mathcal_X Y'' ("Lie derivative of Y along X"). This generalizes to the Lie derivative of any tensor field along the flow generated by ''X''. The Lie bracket is an R- bilinear operation and turns the set of all smooth vector fields on the manifold ''M'' into an (infinite-dimensional) Lie algebra. The Lie bracket plays an important role in differential geometry and differential topology, for instance in the Frobenius integrability theorem, and is also fundamental in the geometric theory of nonlinear control systems., nonholonomic systems; , feedback linearization. Definitio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complexification
In mathematics, the complexification of a vector space over the field of real numbers (a "real vector space") yields a vector space over the complex number field, obtained by formally extending the scaling of vectors by real numbers to include their scaling ("multiplication") by complex numbers. Any basis for (a space over the real numbers) may also serve as a basis for over the complex numbers. Formal definition Let V be a real vector space. The of is defined by taking the tensor product of V with the complex numbers (thought of as a 2-dimensional vector space over the reals): :V^ = V\otimes_ \Complex\,. The subscript, \R, on the tensor product indicates that the tensor product is taken over the real numbers (since V is a real vector space this is the only sensible option anyway, so the subscript can safely be omitted). As it stands, V^ is only a real vector space. However, we can make V^ into a complex vector space by defining complex multiplication as follows: :\alpha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
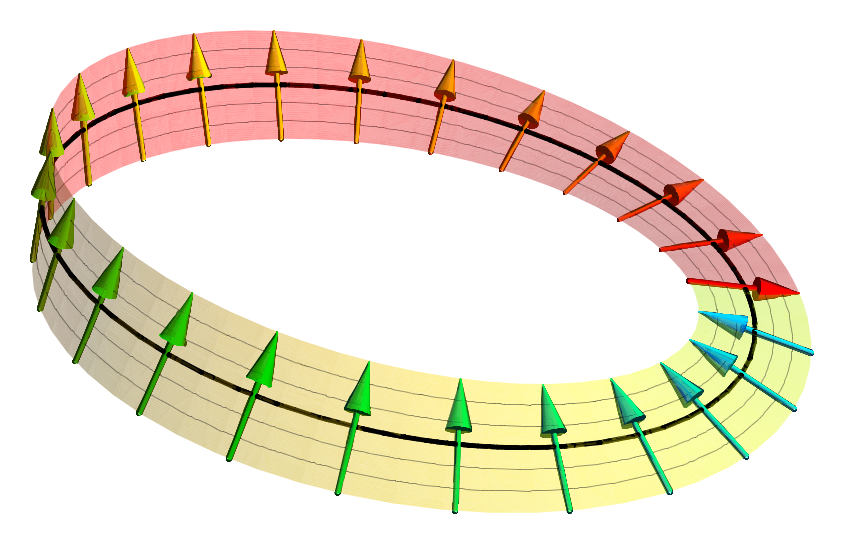
Spinor
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
