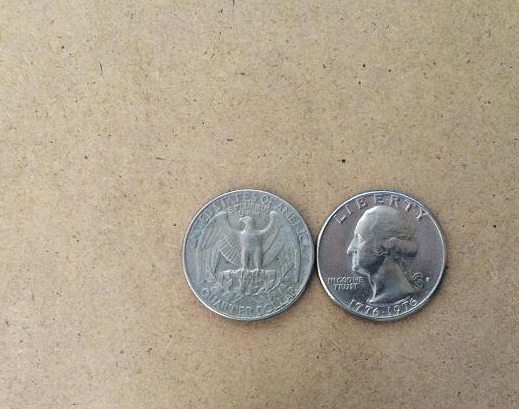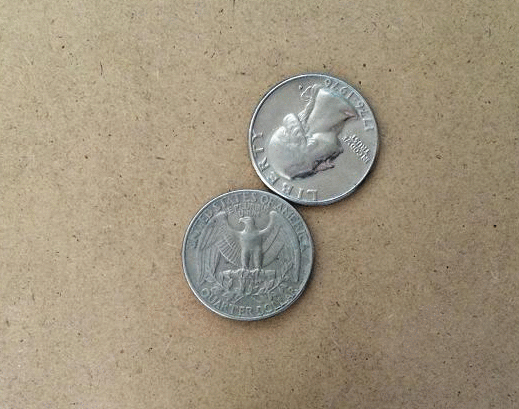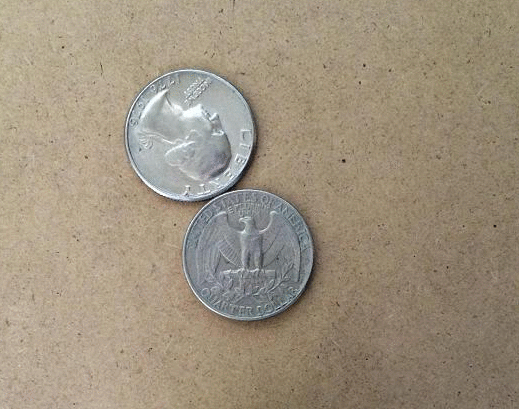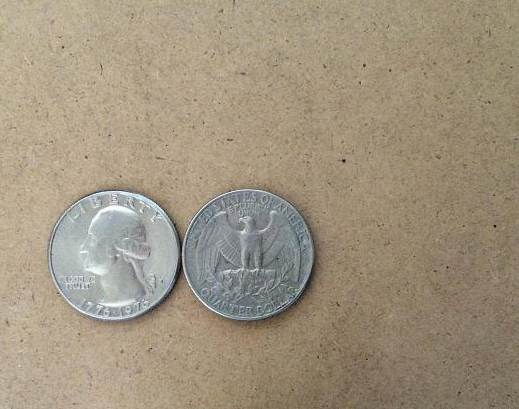|
Coin Rotation Paradox
The coin rotation paradox is the counter-intuitive observation that, when one coin is rolled around the rim of another coin of equal size, the moving coin completes two full rotations after going all the way around the stationary coin. Description Start with two identical coins touching each other on a table, with their "head" sides displayed and parallel. Keeping coin A stationary, rotate coin B around A, keeping a point of contact with no slippage. As coin B reaches the opposite side, the two heads will again be parallel; B has made one revolution. Continuing to move B brings it back to the starting position and completes a second revolution. Paradoxically, coin B appears to have rolled a distance equal to twice its circumference. In reality, as the circumferences of both coins are equal, by definition coin B has only rolled a distance equal to its own circumference. The second rotation arises from the fact that the path along which it has rolled is a circle. This is analogous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coin Rotation Paradox
The coin rotation paradox is the counter-intuitive observation that, when one coin is rolled around the rim of another coin of equal size, the moving coin completes two full rotations after going all the way around the stationary coin. Description Start with two identical coins touching each other on a table, with their "head" sides displayed and parallel. Keeping coin A stationary, rotate coin B around A, keeping a point of contact with no slippage. As coin B reaches the opposite side, the two heads will again be parallel; B has made one revolution. Continuing to move B brings it back to the starting position and completes a second revolution. Paradoxically, coin B appears to have rolled a distance equal to twice its circumference. In reality, as the circumferences of both coins are equal, by definition coin B has only rolled a distance equal to its own circumference. The second rotation arises from the fact that the path along which it has rolled is a circle. This is analogous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coin Rotation Paradox Animation
A coin is a small, flat (usually depending on the country or value), round piece of metal or plastic used primarily as a medium of exchange or legal tender. They are standardized in weight, and produced in large quantities at a mint in order to facilitate trade. They are most often issued by a government. Coins often have images, numerals, or text on them. ''Obverse'' and its opposite, ''reverse'', refer to the two flat faces of coins and medals. In this usage, ''obverse'' means the front face of the object and ''reverse'' means the back face. The obverse of a coin is commonly called ''heads'', because it often depicts the head of a prominent person, and the reverse ''tails''. Coins are usually made of metal or an alloy, or sometimes of man-made materials. They are usually disc shaped. Coins, made of valuable metal, are stored in large quantities as bullion coins. Other coins are used as money in everyday transactions, circulating alongside banknotes. Usually the highest value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sidereal Time
Sidereal time (as a unit also sidereal day or sidereal rotation period) (sidereal ) is a timekeeping system that astronomers use to locate celestial objects. Using sidereal time, it is possible to easily point a telescope to the proper coordinates in the night sky. In short, sidereal time is a "time scale that is based on Earth's rate of rotation measured relative to the fixed stars", or more correctly, relative to the March equinox. Viewed from the same location, a star seen at one position in the sky will be seen at the same position on another night at the same sidereal time. This is similar to how the time kept by a sundial (Solar time) can be used to find the location of the Sun. Just as the Sun and Moon appear to rise in the east and set in the west due to the rotation of Earth, so do the stars. Both Solar time and sidereal time make use of the regularity of Earth's rotation about its polar axis: solar time following the Sun while, roughly speaking, sidereal time follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quora
Quora () is a social question-and-answer website based in Mountain View, California. It was founded on June 25, 2009, and made available to the public on June 21, 2010. Users can collaborate by editing questions and commenting on answers that have been submitted by other users. As of 2020, the website was visited by 300million users a month. History Founding and naming Quora was co-founded by former Facebook employees Adam D'Angelo and Charlie Cheever in June 2009. In an answer to the question "How did Adam D'Angelo and Charlie Cheever come up with the name Quora?" written on Quora in 2011, Charlie Cheever stated, "We spent a few hours brainstorming and writing down all the ideas that we could think of. After consulting with friends and eliminating ones we didn't love, we narrowed it down to 5 or 6 finalists, and eventually settled on Quora." Cheever went on to state, "The closest competition that he nameQuora had was Quiver." 2010–2013: Early growth In March 2010, Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristotle's Wheel Paradox
Aristotle's wheel paradox is a paradox or problem appearing in the Greek work ''Mechanica'', traditionally attributed to Aristotle. It states as follows: A wheel is depicted in two-dimensional space as two circles. Its larger, outer circle is tangential to a horizontal surface (e.g. a road that it rolls on), while the smaller, inner one has the same center and is rigidly affixed to the larger. (The smaller circle could be the bead of a tire, the rim it is mounted upon, or the axle.) Assuming the larger circle rolls without slipping (or skidding) for one full revolution, the distances moved by both circles' circumferences are the same. The distance travelled by the larger circle is equal to its circumference, but for the smaller it is greater than its circumference, thereby creating a paradox. The paradox is not limited to wheels: other things depicted in two dimensions display the same behavior such as a roll of tape, or a typical round bottle or jar rolled on its side (the smalle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by de Castillon in 1741 but the cardioid had been the subject of study decades beforehand.Yates Named for its heart-like form, it is shaped more like the outline of the cross section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone which is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solar Day
A synodic day (or synodic rotation period or solar day) is the period for a celestial object to rotate once in relation to the star it is orbiting, and is the basis of solar time. The synodic day is distinguished from the sidereal day, which is one complete rotation in relation to distant stars, which is the basis of sidereal time. This is different from the duration of a synodic day because the revolution of the body around its parent star would cause a single "day" to pass relative to a star, even if the body did not rotate itself. Earth's synodic day Earth's synodic day is the time it takes for the Sun to pass over the same meridian (a line of longitude) on consecutive days, whereas a sidereal day is the time it takes for a given distant star to pass over a meridian on consecutive days. For example, in the Northern Hemisphere, a synodic day could be measured as the time taken for the Sun to move from exactly true south (i.e. its highest declination) on one day to exactly s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sidereal Day
Sidereal time (as a unit also sidereal day or sidereal rotation period) (sidereal ) is a timekeeping system that astronomers use to locate celestial objects. Using sidereal time, it is possible to easily point a telescope to the proper coordinates in the night sky. In short, sidereal time is a "time scale that is based on Earth's rate of rotation measured relative to the fixed stars", or more correctly, relative to the March equinox. Viewed from the same location, a star seen at one position in the sky will be seen at the same position on another night at the same sidereal time. This is similar to how the time kept by a sundial (Solar time) can be used to find the location of the Sun. Just as the Sun and Moon appear to rise in the east and set in the west due to the rotation of Earth, so do the stars. Both Solar time and sidereal time make use of the regularity of Earth's rotation about its polar axis: solar time following the Sun while, roughly speaking, sidereal time follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Polygon
The term ''complex polygon'' can mean two different things: * In geometry, a polygon in the unitary plane, which has two complex dimensions. * In computer graphics, a polygon whose boundary is not simple. Geometry In geometry, a complex polygon is a polygon in the complex Hilbert plane, which has two complex dimensions. A complex number may be represented in the form (a + ib), where a and b are real numbers, and i is the square root of -1. Multiples of i such as ib are called ''imaginary numbers''. A complex number lies in a complex plane having one real and one imaginary dimension, which may be represented as an Argand diagram. So a single complex dimension comprises two spatial dimensions, but of different kinds - one real and the other imaginary. The unitary plane comprises two such complex planes, which are orthogonal to each other. Thus it has two real dimensions and two imaginary dimensions. A complex polygon is a (complex) two-dimensional (i.e. four spatial dimensions) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Winding Number
In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise. Winding numbers are fundamental objects of study in algebraic topology, and they play an important role in vector calculus, complex analysis, geometric topology, differential geometry, and physics (such as in string theory). Intuitive description Suppose we are given a closed, oriented curve in the ''xy'' plane. We can imagine the curve as the path of motion of some object, with the orientation indicating the direction in which the object moves. Then the winding number of the curve is equal to the total number of counterclockwise turns that the object makes around the origin. When counting the total nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Polygon
In geometry, a simple polygon is a polygon that does not Intersection (Euclidean geometry), intersect itself and has no holes. That is, it is a flat shape consisting of straight, non-intersecting line segments or "sides" that are joined pairwise to form a single closed curve, closed path. If the sides intersect then the polygon is not simple. The qualifier "simple" is frequently omitted, with the above definition then being understood to define a polygon in general. The definition given above ensures the following properties: * A polygon encloses a region (mathematics), region (called its interior) which always has a measurable area. * The line segments that make up a polygon (called sides or edges) meet only at their endpoints, called vertices (singular: vertex) or less formally "corners". * Exactly two edges meet at each vertex. * The number of edges always equals the number of vertices. Two edges meeting at a corner are usually required to form an angle that is not straight ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
