|
Bregman Divergence
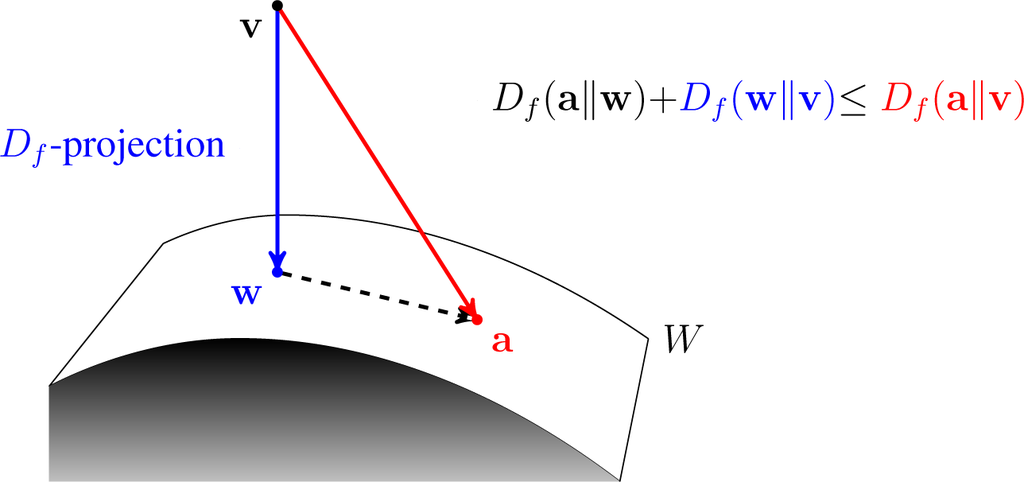
In mathematics, specifically statistics and information geometry, a Bregman divergence or Bregman distance is a measure of difference between two points, defined in terms of a strictly convex function; they form an important class of divergences. When the points are interpreted as probability distributions – notably as either values of the parameter of a parametric model or as a data set of observed values – the resulting distance is a statistical distance. The most basic Bregman divergence is the squared Euclidean distance. Bregman divergences are similar to metrics, but satisfy neither the triangle inequality (ever) nor symmetry (in general). However, they satisfy a generalization of the Pythagorean theorem, and in information geometry the corresponding statistical manifold is interpreted as a (dually) flat manifold. This allows many techniques of optimization theory to be generalized to Bregman divergences, geometrically as generalizations of least squares. Bregman divergenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty). For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary of a convex set is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to , 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper "A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Processing Inequality
The data processing inequality is an information theoretic concept which states that the information content of a signal cannot be increased via a local physical operation. This can be expressed concisely as 'post-processing cannot increase information'. Definition Let three random variables form the Markov chain X \rightarrow Y \rightarrow Z, implying that the conditional distribution of Z depends only on Y and is conditionally independent of X. Specifically, we have such a Markov chain if the joint probability mass function can be written as :p(x,y,z) = p(x)p(y, x)p(z, y)=p(y)p(x, y)p(z, y) In this setting, no processing of Y, deterministic or random, can increase the information that Y contains about X. Using the mutual information, this can be written as : : I(X;Y) \geqslant I(X;Z) With the equality I(X;Y) = I(X;Z) if and only if I(X;Y\mid Z)=0 , i.e. Z and Y contain the same information about X, and X \rightarrow Z \rightarrow Y also forms a Markov chain. Proof One can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how one probability distribution ''P'' is different from a second, reference probability distribution ''Q''. A simple interpretation of the KL divergence of ''P'' from ''Q'' is the expected excess surprise from using ''Q'' as a model when the actual distribution is ''P''. While it is a distance, it is not a metric, the most familiar type of distance: it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for certain classes of distributions (notably an exponential family), it satisfies a generalized Pythagorean theorem (which applies to squared distances). In the simple case, a relative entropy of 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-divergence
In probability theory, an f-divergence is a function D_f(P\, Q) that measures the difference between two probability distributions P and Q. Many common divergences, such as KL-divergence, Hellinger distance, and total variation distance, are special cases of f-divergence. History These divergences were introduced by Alfréd Rényi in the same paper where he introduced the well-known Rényi entropy. He proved that these divergences decrease in Markov processes. ''f''-divergences were studied further independently by , and and are sometimes known as Csiszár f-divergences, Csiszár-Morimoto divergences, or Ali-Silvey distances. Definition Non-singular case Let P and Q be two probability distributions over a space \Omega, such that P\ll Q, that is, P is absolutely continuous with respect to Q. Then, for a convex function f: , \infty)\to(-\infty, \infty/math> such that f(x) is finite for all x > 0, f(1)=0, and f(0)=\lim_ f(t) (which could be infinite), the f-divergence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bregman Divergence Diagram Used In Proof Of Squared Generalized Euclidean Distances
Bregman is a surname. Notable people with the surname include: *Ahron Bregman (born 1958), British-Israeli political scientist, writer and journalist, specialising on the Arab-Israeli conflict *Albert Bregman (born 1936), Canadian psychologist, professor emeritus at McGill University * Alex Bregman (born 1994), American baseball player *Buddy Bregman (1930–2017), American musical arranger, record producer and composer * James Bregman (born 1941), member of the first American team to compete in judo in the Summer Olympics *Lev M. Bregman (born 1941), Russian mathematician, most known for the Bregman divergence named after him. *Martin Bregman (1926–2018), American film producer and former personal manager *Myriam Bregman (born 1972), Argentine politician *Rutger Bregman (born 1988), Dutch historian * Solomon Bregman (1895–1953), prominent member of the Jewish Anti-Fascist Committee formed in the Soviet Union in 1942 *Tracey E. Bregman (born 1963), German-American soap opera actr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Definiteness
In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite function * Positive-definite function on a group * Positive-definite functional * Positive-definite kernel * Positive-definite matrix * Positive-definite quadratic form In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite fu ... References *. *. {{Set index article, mathematics Quadratic forms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mahalanobis Distance
The Mahalanobis distance is a measure of the distance between a point ''P'' and a distribution ''D'', introduced by P. C. Mahalanobis in 1936. Mahalanobis's definition was prompted by the problem of identifying the similarities of skulls based on measurements in 1927. It is a multi-dimensional generalization of the idea of measuring how many standard deviations away ''P'' is from the mean of ''D''. This distance is zero for ''P'' at the mean of ''D'' and grows as ''P'' moves away from the mean along each principal component axis. If each of these axes is re-scaled to have unit variance, then the Mahalanobis distance corresponds to standard Euclidean distance in the transformed space. The Mahalanobis distance is thus unitless, scale-invariant, and takes into account the correlations of the data set. Definition Given a probability distribution Q on \R^N, with mean \vec = (\mu_1, \mu_2, \mu_3, \dots , \mu_N)^\mathsf and positive-definite covariance matrix S, the Mahalanobis dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jensen's Inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations. Jensen's inequality generalizes the statement that the secant line of a convex function lies ''above'' the graph of the function, which is Jensen's inequality for two points: the secant line consists of weighted means of the convex function (for ''t'' ∈ ,1, :t f(x_1) + (1-t) f(x_2), while t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Interior
In mathematics, the relative interior of a set is a refinement of the concept of the interior, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces. Formally, the relative interior of a set S (denoted \operatorname(S)) is defined as its interior within the affine hull of S. In other words, \operatorname(S) := \, where \operatorname(S) is the affine hull of S, and N_\epsilon(x) is a ball of radius \epsilon centered on x. Any metric can be used for the construction of the ball; all metrics define the same set as the relative interior. For any nonempty convex set In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex ... C \subseteq \mathbb^n the relative interior can be defined as \operatorname(C) := \. Comparison to interior * The int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bregman Divergence Pythagorean
Bregman is a surname. Notable people with the surname include: *Ahron Bregman (born 1958), British-Israeli political scientist, writer and journalist, specialising on the Arab-Israeli conflict *Albert Bregman (born 1936), Canadian psychologist, professor emeritus at McGill University * Alex Bregman (born 1994), American baseball player *Buddy Bregman (1930–2017), American musical arranger, record producer and composer * James Bregman (born 1941), member of the first American team to compete in judo in the Summer Olympics *Lev M. Bregman (born 1941), Russian mathematician, most known for the Bregman divergence named after him. *Martin Bregman (1926–2018), American film producer and former personal manager *Myriam Bregman (born 1972), Argentine politician *Rutger Bregman (born 1988), Dutch historian * Solomon Bregman (1895–1953), prominent member of the Jewish Anti-Fascist Committee formed in the Soviet Union in 1942 *Tracey E. Bregman (born 1963), German-American soap opera actr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |