|
Bellman Pseudospectral Method
The Bellman pseudospectral method is a pseudospectral method for optimal control based on Bellman's principle of optimality. It is part of the larger theory of pseudospectral optimal control, a term coined by Ross. The method is named after Richard E. Bellman. It was introduced by Ross et al.I. M. Ross, Q. Gong and P. Sekhavat, The Bellman pseudospectral method, AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, Hawaii, AIAA-2008-6448, August 18–21, 2008. first as a means to solve multiscale optimal control problems, and later expanded to obtain suboptimal solutions for general optimal control problems. Theoretical foundations The multiscale version of the Bellman pseudospectral method is based on the spectral convergence property of the Ross–Fahroo pseudospectral methods. That is, because the Ross–Fahroo pseudospectral method converges at an exponentially fast rate, pointwise convergence to a solution is obtained at very low number of nodes even when the so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudospectral Method
Pseudo-spectral methods, also known as discrete variable representation (DVR) methods, are a class of numerical methods used in applied mathematics and scientific computing for the solution of partial differential equations. They are closely related to spectral methods, but complement the basis by an additional pseudo-spectral basis, which allows representation of functions on a quadrature grid. This simplifies the evaluation of certain operators, and can considerably speed up the calculation when using fast algorithms such as the fast Fourier transform. Motivation with a concrete example Take the initial-value problem :i \frac \psi(x, t) = \Bigl \frac + V(x) \Bigr\psi(x,t), \qquad\qquad \psi(t_0) = \psi_0 with periodic conditions \psi(x+1, t) = \psi(x, t). This specific example is the Schrödinger equation for a particle in a potential V(x), but the structure is more general. In many practical partial differential equations, one has a term that involves derivatives (such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Control
Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory. Optimal control is an extension of the calculus of variations, and is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and Richard Bellman in the 1950s, after contributions to calc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
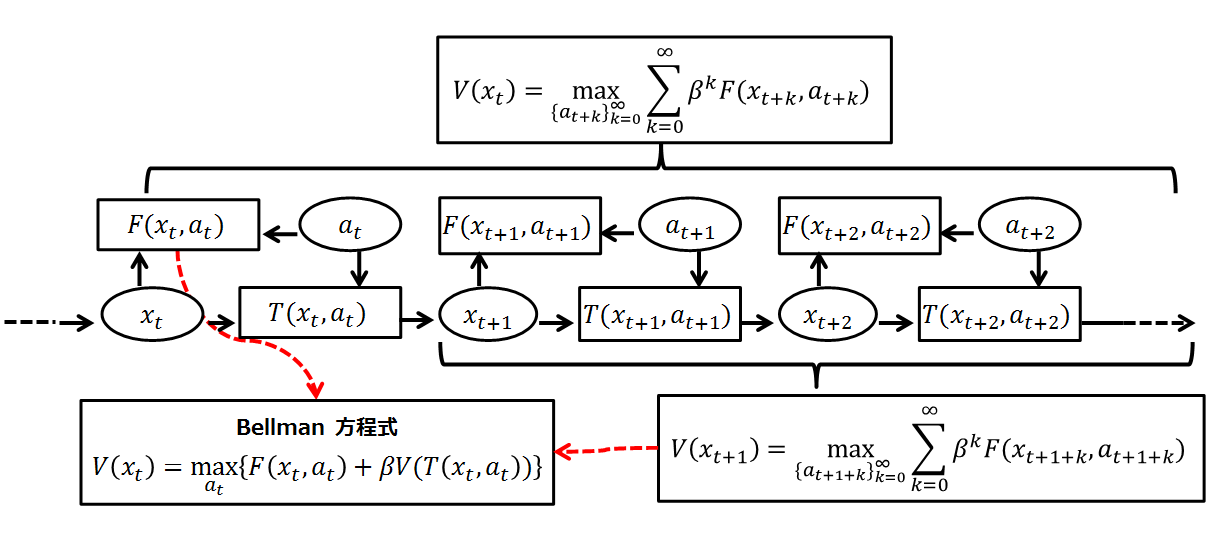
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's '' Theory of Games and Econ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudospectral Optimal Control
Pseudospectral optimal control is a joint theoretical-computational method for solving optimal control problems. It combines pseudospectral (PS) theory with optimal control theory to produce PS optimal control theory. PS optimal control theory has been used in ground and flight systems in military and industrial applications. The techniques have been extensively used to solve a wide range of problems such as those arising in UAV trajectory generation, missile guidance, control of robotic arms, vibration damping, lunar guidance, magnetic control, swing-up and stabilization of an inverted pendulum, orbit transfers, tether libration control, ascent guidance and quantum control. Overview There are a very large number of ideas that fall under the general banner of pseudospectral optimal control. Examples of these are the Legendre pseudospectral method, the Chebyshev pseudospectral method, the Gauss pseudospectral method, the Ross-Fahroo pseudospectral method, the Bellman pseudos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard E
Richard is a male given name. It originates, via Old French, from Frankish language, Old Frankish and is a Compound (linguistics), compound of the words descending from Proto-Germanic language, Proto-Germanic ''*rīk-'' 'ruler, leader, king' and ''*hardu-'' 'strong, brave, hardy', and it therefore means 'strong in rule'. Nicknames include "Richie", "Dick (nickname), Dick", "Dickon", "Dickie (name), Dickie", "Rich (given name), Rich", "Rick (given name), Rick", "Rico (name), Rico", "Ricky (given name), Ricky", and more. Richard is a common English, German and French male name. It's also used in many more languages, particularly Germanic, such as Norwegian, Danish, Swedish, Icelandic, and Dutch, as well as other languages including Irish, Scottish, Welsh and Finnish. Richard is cognate with variants of the name in other European languages, such as the Swedish "Rickard", the Catalan "Ricard" and the Italian "Riccardo", among others (see comprehensive variant list below). People ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ross–Fahroo Pseudospectral Method
Introduced by I. Michael Ross and F. Fahroo, the Ross–Fahroo pseudospectral methods are a broad collection of pseudospectral methods for optimal control.N. Bedrossian, M. Karpenko, and S. Bhatt, "Overclock My Satellite: Sophisticated Algorithms Boost Satellite Performance on the Cheap", ''IEEE Spectrum'', November 2012. I. M. Ross and F. Fahroo, A Pseudospectral Transformation of the Covectors of Optimal Control Systems, Proceedings of the First IFAC Symposium on System Structure and Control, Prague, Czech Republic, 29–31 August 2001. I. M. Ross and F. Fahroo, Legendre Pseudospectral Approximations of Optimal Control Problems, ''Lecture Notes in Control and Information Sciences'', Vol. 295, Springer-Verlag, 2003. I. M. Ross and F. Fahroo, Discrete Verification of Necessary Conditions for Switched Nonlinear Optimal Control Systems, Proceedings of the American Control Conference, Invited Paper, June 2004, Boston, MA. Examples of the Ross–Fahroo pseudospectral methods are th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aliasing
In signal processing and related disciplines, aliasing is an effect that causes different signals to become indistinguishable (or ''aliases'' of one another) when sampled. It also often refers to the distortion or artifact that results when a signal reconstructed from samples is different from the original continuous signal. Aliasing can occur in signals sampled in time, for instance digital audio, or the stroboscopic effect, and is referred to as temporal aliasing. It can also occur in spatially sampled signals (e.g. moiré patterns in digital images); this type of aliasing is called spatial aliasing. Aliasing is generally avoided by applying low-pass filters or anti-aliasing filters (AAF) to the input signal before sampling and when converting a signal from a higher to a lower sampling rate. Suitable reconstruction filtering should then be used when restoring the sampled signal to the continuous domain or converting a signal from a lower to a higher sampling rate. For spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist–Shannon Sampling Theorem
The Nyquist–Shannon sampling theorem is a theorem in the field of signal processing which serves as a fundamental bridge between continuous-time signals and discrete-time signals. It establishes a sufficient condition for a sample rate that permits a discrete sequence of ''samples'' to capture all the information from a continuous-time signal of finite bandwidth. Strictly speaking, the theorem only applies to a class of mathematical functions having a Fourier transform that is zero outside of a finite region of frequencies. Intuitively we expect that when one reduces a continuous function to a discrete sequence and interpolates back to a continuous function, the fidelity of the result depends on the density (or sample rate) of the original samples. The sampling theorem introduces the concept of a sample rate that is sufficient for perfect fidelity for the class of functions that are band-limited to a given bandwidth, such that no actual information is lost in the sampling proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pontryagin's Minimum Principle
Pontryagin's maximum principle is used in optimal control theory to find the best possible control for taking a dynamical system from one state to another, especially in the presence of constraints for the state or input controls. It states that it is necessary for any optimal control along with the optimal state trajectory to solve the so-called Hamiltonian system, which is a two-point boundary value problem, plus a maximum condition of the control Hamiltonian. These necessary conditions become sufficient under certain convexity conditions on the objective and constraint functions. The maximum principle was formulated in 1956 by the Russian mathematician Lev Pontryagin and his students, and its initial application was to the maximization of the terminal speed of a rocket. The result was derived using ideas from the classical calculus of variations. After a slight perturbation of the optimal control, one considers the first-order term of a Taylor expansion with respect to the pert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Pseudospectral Method
The Legendre pseudospectral method for optimal control problems is based on Legendre polynomials. It is part of the larger theory of pseudospectral optimal control, a term coined by Ross. A basic version of the Legendre pseudospectral was originally proposed by Elnagar and his coworkers in 1995.G. Elnagar, M. A. Kazemi, and M. Razzaghi, "The Pseudospectral Legendre Method for Discretizing Optimal Control Problems," ''IEEE Transactions on Automatic Control,'' 40:1793–1796, 1995. Since then, Ross, Fahroo and their coworkers have extended, generalized and applied the method for a large range of problems.Q. Gong, W. Kang, N. Bedrossian, F. Fahroo, P. Sekhavat and K. Bollino, "Pseudospectral Optimal Control for Military and Industrial Applications," ''46th IEEE Conference on Decision and Control,'' New Orleans, LA, pp. 4128–4142, Dec. 2007. An application that has received wide publicity is the use of their method for generating real time trajectories for the International Space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Pseudospectral Method
The Chebyshev pseudospectral method for optimal control problems is based on Chebyshev polynomials of the first kind. It is part of the larger theory of pseudospectral optimal control, a term coined by Ross. Unlike the Legendre pseudospectral method, the Chebyshev pseudospectral (PS) method does not immediately offer high-accuracy quadrature solutions. Consequently, two different versions of the method have been proposed: one by Elnagar et al., and another by Fahroo and Ross. The two versions differ in their quadrature techniques. The Fahroo–Ross method is more commonly used today due to the ease in implementation of the Clenshaw–Curtis quadrature technique (in contrast to Elnagar–Kazemi's cell-averaging method). In 2008, Trefethen showed that the Clenshaw–Curtis method was nearly as accurate as Gauss quadrature. This breakthrough result opened the door for a covector mapping theorem for Chebyshev PS methods. A complete mathematical theory for Chebyshev PS methods was fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudospectral Knotting Method
In applied mathematics, the pseudospectral knotting method is a generalization and enhancement of a standard pseudospectral method for optimal control. The concept was introduced by I. Michael Ross and F. Fahroo in 2004, and forms part of the collection of the Ross–Fahroo pseudospectral methods.Ross, I. M. and Fahroo, F., Pseudospectral Knotting Methods for Solving Optimal Control Problems, ''Journal of Guidance, Control and Dynamics,'' Vol. 27, No. 3, pp. 397–405, 2004. Definition According to Ross and Fahroo a pseudospectral (PS) knot is a double Lobatto point; i.e. two boundary points on top of one another. At this point, information (such as discontinuities, jumps, dimension changes etc.) is exchanged between two standard PS methods. This information exchange is used to solve some of the most difficult problems in optimal control known as hybrid optimal control problems.Ross, I. M. and D’Souza, C. N., A Hybrid Optimal Control Framework for Mission Planning, ''Journal o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |