Bellman equation

A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.

The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's '' Theory of Games and Economic Behavior'' and Abraham Wald's ''sequential analysis''. The term "Bellman equation" usually refers to the dynamic programming equation (DPE) associated with discrete-time optimization problems. In continuous-time optimization problems, the analogous equation is a partial differential equation that is called the Hamilton–Jacobi–Bellman equation.

In discrete time any multi-stage optimization problem can be solved by analyzing the appropriate Bellman equation. The appropriate Bellman equation can be found by introducing new state variables (state augmentation). However, the resulting augmented-state multi-stage optimization problem has a higher dimensional state space than the original multi-stage optimization problem - an issue that can potentially render the augmented problem intractable due to the “ curse of dimensionality”. Alternatively, it has been shown that if the cost function of the multi-stage optimization problem satisfies a "backward separable" structure, then the appropriate Bellman equation can be found without state augmentation.

Analytical concepts in dynamic programming

To understand the Bellman equation, several underlying concepts must be understood. First, any optimization problem has some objective: minimizing travel time, minimizing cost, maximizing profits, maximizing utility, etc. The mathematical function that describes this objective is called the ''objective function''.

Dynamic programming breaks a multi-period planning problem into simpler steps at different points in time. Therefore, it requires keeping track of how the decision situation is evolving over time. The information about the current situation that is needed to make a correct decision is called the "state". For example, to decide how much to consume and spend at each point in time, people would need to know (among other things) their initial wealth. Therefore, wealth $(W)$ would be one of their ''state variables'', but there would probably be others.

The variables chosen at any given point in time are often called the '' control variables''. For instance, given their current wealth, people might decide how much to consume now. Choosing the control variables now may be equivalent to choosing the next state; more generally, the next state is affected by other factors in addition to the current control. For example, in the simplest case, today's wealth (the state) and consumption (the control) might exactly determine tomorrow's wealth (the new state), though typically other factors will affect tomorrow's wealth too.

The dynamic programming approach describes the optimal plan by finding a rule that tells what the controls should be, given any possible value of the state. For example, if consumption (''c'') depends ''only'' on wealth (''W''), we would seek a rule $c(W)$ that gives consumption as a function of wealth. Such a rule, determining the controls as a function of the states, is called a ''policy function''.

Finally, by definition, the optimal decision rule is the one that achieves the best possible value of the objective. For example, if someone chooses consumption, given wealth, in order to maximize happiness (assuming happiness ''H'' can be represented by a mathematical function, such as a utility function and is something defined by wealth), then each level of wealth will be associated with some highest possible level of happiness, $H(W)$. The best possible value of the objective, written as a function of the state, is called the ''value function''.

Bellman showed that a dynamic optimization problem in discrete time can be stated in a recursive, step-by-step form known as backward induction by writing down the relationship between the value function in one period and the value function in the next period. The relationship between these two value functions is called the "Bellman equation". In this approach, the optimal policy in the last time period is specified in advance as a function of the state variable's value at that time, and the resulting optimal value of the objective function is thus expressed in terms of that value of the state variable. Next, the next-to-last period's optimization involves maximizing the sum of that period's period-specific objective function and the optimal value of the future objective function, giving that period's optimal policy contingent upon the value of the state variable as of the next-to-last period decision. This logic continues recursively back in time, until the first period decision rule is derived, as a function of the initial state variable value, by optimizing the sum of the first-period-specific objective function and the value of the second period's value function, which gives the value for all the future periods. Thus, each period's decision is made by explicitly acknowledging that all future decisions will be optimally made.

Derivation

A dynamic decision problem

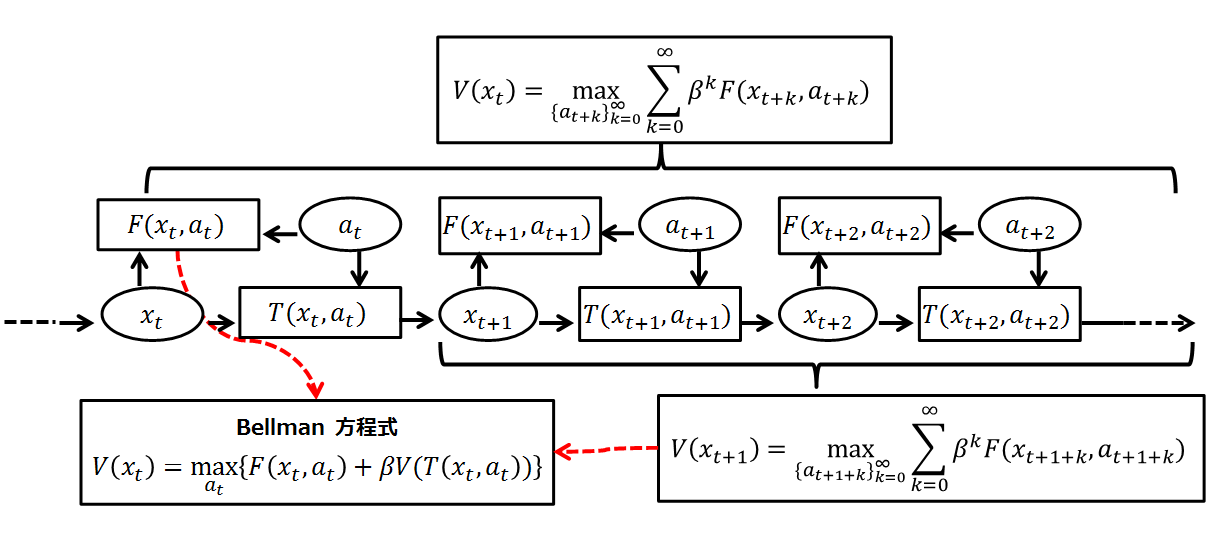
Let $x_t$ be the state at time $t$. For a decision that begins at time 0, we take as given the initial state $x_0$. At any time, the set of possible actions depends on the current state; we express this as $a_ \in \Gamma (x_t)$, where a particular action $a_t$ represents particular values for one or more control variables, and $\Gamma (x_t)$ is the set of actions available to be taken at state $x_t$. It is also assumed that the state changes from $x$ to a new state $T(x,a)$ when action $a$ is taken, and that the current payoff from taking action $a$ in state $x$ is $F(x,a)$. Finally, we assume impatience, represented by a discount factor $0<\beta<1$.

Under these assumptions, an infinite-horizon decision problem takes the following form:

:$V(x_0) \; = \; \max_ \sum_^ \beta^t F(x_t,a_),$

subject to the constraints

:$a_ \in \Gamma (x_t), \; x_=T(x_t,a_t), \; \forall t = 0, 1, 2, \dots$

Notice that we have defined notation $V(x_0)$ to denote the optimal value that can be obtained by maximizing this objective function subject to the assumed constraints. This function is the ''value function''. It is a function of the initial state variable $x_0$, since the best value obtainable depends on the initial situation.

Bellman's principle of optimality

The dynamic programming method breaks this decision problem into smaller subproblems. Bellman's ''principle of optimality'' describes how to do this:

Principle of Optimality: An optimal policy has the property that whatever the initial state and initial decision are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision. (See Bellman, 1957, Chap. III.3.)

In computer science, a problem that can be broken apart like this is said to have optimal substructure. In the context of dynamic game theory, this principle is analogous to the concept of subgame perfect equilibrium, although what constitutes an optimal policy in this case is conditioned on the decision-maker's opponents choosing similarly optimal policies from their points of view.

As suggested by the ''principle of optimality'', we will consider the first decision separately, setting aside all future decisions (we will start afresh from time 1 with the new state $x_1$). Collecting the future decisions in brackets on the right, the above infinite-horizon decision problem is equivalent to:

:$\max_ \left \$

subject to the constraints

:$a_0 \in \Gamma (x_0), \; x_1=T(x_0,a_0).$

Here we are choosing $a_0$, knowing that our choice will cause the time 1 state to be $x_1=T(x_0,a_0)$. That new state will then affect the decision problem from time 1 on. The whole future decision problem appears inside the square brackets on the right.

The Bellman equation

So far it seems we have only made the problem uglier by separating today's decision from future decisions. But we can simplify by noticing that what is inside the square brackets on the right is ''the value'' of the time 1 decision problem, starting from state $x_1=T(x_0,a_0)$.

Therefore, the problem can be rewritten as a recursive definition of the value function:

:$V(x_0) = \max_ \$, subject to the constraints: $a_0 \in \Gamma (x_0), \; x_1=T(x_0,a_0).$

This is the Bellman equation. It may be simplified even further if the time subscripts are dropped and the value of the next state is plugged in:

:$V(x) = \max_ \.$

The Bellman equation is classified as a functional equation, because solving it means finding the unknown function $V$, which is the ''value function''. Recall that the value function describes the best possible value of the objective, as a function of the state $x$. By calculating the value function, we will also find the function $a(x)$ that describes the optimal action as a function of the state; this is called the ''policy function''.

In a stochastic problem

In the deterministic setting, other techniques besides dynamic programming can be used to tackle the above optimal control problem. However, the Bellman Equation is often the most convenient method of solving ''stochastic'' optimal control problems.

For a specific example from economics, consider an infinitely-lived consumer with initial wealth endowment $$ at period $0$. They have an instantaneous utility function $u(c)$ where $c$ denotes consumption and discounts the next period utility at a rate of $0< \beta<1$. Assume that what is not consumed in period $t$ carries over to the next period with interest rate $r$. Then the consumer's utility maximization problem is to choose a consumption plan $\$ that solves

:$\max \sum_ ^ \beta^t u ()$

subject to

:$= (1 + r) ( - ), \; \geq 0,$

and

:$\lim_ \geq 0.$

The first constraint is the capital accumulation/law of motion specified by the problem, while the second constraint is a transversality condition that the consumer does not carry debt at the end of their life. The Bellman equation is

:$V(a) = \max_ \,$

Alternatively, one can treat the sequence problem directly using, for example, the Hamiltonian equations.

Now, if the interest rate varies from period to period, the consumer is faced with a stochastic optimization problem. Let the interest ''r'' follow a Markov process with probability transition function $Q(r, d\mu_r)$ where $d\mu_r$ denotes the probability measure governing the distribution of interest rate next period if current interest rate is $r$. In this model the consumer decides their current period consumption after the current period interest rate is announced.

Rather than simply choosing a single sequence $\$, the consumer now must choose a sequence $\$ for each possible realization of a $\$ in such a way that their lifetime expected utility is maximized:

:$\max_ \mathbb\bigg( \sum_ ^ \beta^t u () \bigg).$

The expectation $\mathbb$ is taken with respect to the appropriate probability measure given by ''Q'' on the sequences of ''r''s. Because ''r'' is governed by a Markov process, dynamic programming simplifies the problem significantly. Then the Bellman equation is simply:

:$V(a, r) = \max_ \ .$

Under some reasonable assumption, the resulting optimal policy function ''g''(''a'',''r'') is measurable.

For a general stochastic sequential optimization problem with Markovian shocks and where the agent is faced with their decision '' ex-post'', the Bellman equation takes a very similar form

:$V(x, z) = \max_ \.$

Solution methods

* The method of undetermined coefficients, also known as 'guess and verify', can be used to solve some infinite-horizon, autonomous Bellman equations.
* The Bellman equation can be solved by backwards induction, either analytically in a few special cases, or numerically on a computer. Numerical backwards induction is applicable to a wide variety of problems, but may be infeasible when there are many state variables, due to the curse of dimensionality. Approximate dynamic programming has been introduced by D. P. Bertsekas and J. N. Tsitsiklis with the use of artificial neural networks ( multilayer perceptrons) for approximating the Bellman function. This is an effective mitigation strategy for reducing the impact of dimensionality by replacing the memorization of the complete function mapping for the whole space domain with the memorization of the sole neural network parameters. In particular, for continuous-time systems, an approximate dynamic programming approach that combines both policy iterations with neural networks was introduced. In discrete-time, an approach to solve the HJB equation combining value iterations and neural networks was introduced.
* By calculating the first-order conditions associated with the Bellman equation, and then using the envelope theorem to eliminate the derivatives of the value function, it is possible to obtain a system of difference equations or differential equations called the ' Euler equations'. Standard techniques for the solution of difference or differential equations can then be used to calculate the dynamics of the state variables and the control variables of the optimization problem.

Applications in economics

The first known application of a Bellman equation in economics is due to Martin Beckmann and Richard Muth. Martin Beckmann also wrote extensively on consumption theory using the Bellman equation in 1959. His work influenced Edmund S. Phelps, among others.

A celebrated economic application of a Bellman equation is Robert C. Merton's seminal 1973 article on the intertemporal capital asset pricing model. (See also Merton's portfolio problem). The solution to Merton's theoretical model, one in which investors chose between income today and future income or capital gains, is a form of Bellman's equation. Because economic applications of dynamic programming usually result in a Bellman equation that is a difference equation, economists refer to dynamic programming as a "recursive method" and a subfield of recursive economics is now recognized within economics.

Nancy Stokey, Robert E. Lucas, and Edward Prescott describe stochastic and nonstochastic dynamic programming in considerable detail, and develop theorems for the existence of solutions to problems meeting certain conditions. They also describe many examples of modeling theoretical problems in economics using recursive methods. This book led to dynamic programming being employed to solve a wide range of theoretical problems in economics, including optimal economic growth, resource extraction, principal–agent problems, public finance, business investment, asset pricing, factor supply, and industrial organization. Lars Ljungqvist and Thomas Sargent apply dynamic programming to study a variety of theoretical questions in monetary policy, fiscal policy, taxation, economic growth, search theory, and labor economics. Avinash Dixit and Robert Pindyck showed the value of the method for thinking about capital budgeting. Anderson adapted the technique to business valuation, including privately held businesses.

Using dynamic programming to solve concrete problems is complicated by informational difficulties, such as choosing the unobservable discount rate. There are also computational issues, the main one being the curse of dimensionality arising from the vast number of possible actions and potential state variables that must be considered before an optimal strategy can be selected. For an extensive discussion of computational issues, see Miranda and Fackler, and Meyn 2007. Appendix contains abridge
Meyn & Tweedie
.

Example

In Markov decision processes, a Bellman equation is a recursion for expected rewards. For example, the expected reward for being in a particular state ''s'' and following some fixed policy $\pi$ has the Bellman equation:

:$V^\pi(s)= R(s,\pi(s)) + \gamma \sum_ P(s', s,\pi(s)) V^\pi(s').\$

This equation describes the expected reward for taking the action prescribed by some policy $\pi$.

The equation for the optimal policy is referred to as the ''Bellman optimality equation'':

:$V^(s)= \max_a \left\.\$

where $$ is the optimal policy and $V^$ refers to the value function of the optimal policy. The equation above describes the reward for taking the action giving the highest expected return.

See also

*
*
*
*
*
*
*
*

References

{{DEFAULTSORT:Bellman Equation
Equations
Dynamic programming
Control theory