|
Hamiltonian (control Theory)
The Hamiltonian is a function used to solve a problem of optimal control for a dynamical system. It can be understood as an instantaneous increment of the Lagrangian expression of the problem that is to be optimized over a certain time period. Inspired by, but distinct from, the Hamiltonian of classical mechanics, the Hamiltonian of optimal control theory was developed by Lev Pontryagin as part of his maximum principle. Pontryagin proved that a necessary condition for solving the optimal control problem is that the control should be chosen so as to optimize the Hamiltonian. Problem statement and definition of the Hamiltonian Consider a dynamical system of n first-order differential equations :\dot(t) = \mathbf(\mathbf(t),\mathbf(t),t) where \mathbf(t) = \left x_(t), x_(t), \ldots, x_(t) \right denotes a vector of state variables, and \mathbf(t) = \left u_(t), u_(t), \ldots, u_(t) \right a vector of control variables. Once initial conditions \mathbf(t_) = \mathbf_ and controls \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Derivative
In mathematics, the total derivative of a function at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when is a function of several variables, because when is a function of a single variable, the total derivative is the same as the ordinary derivative of the function. The total derivative as a linear map Let U \subseteq \R^n be an open subset. Then a function f:U \to \R^m is said to be (totally) differentiable at a point a\in U if there exists a linear transformation df_a:\R^n \to \R^m such that :\lim_ \frac=0. The linear map df_a is called the (total) derivative or (total) differential of f at a. Other notations for the total derivative inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felicity Function
Felicity may refer to: Places * Felicity, California, United States, an unincorporated community * Felicity, Ohio, United States, a village * Felicity, Trinidad and Tobago, a community in Chaguanas Entertainment * ''Felicity'' (TV series), an American drama * ''Felicity'' (film), a 1978 Australian sexploitation film * '' Felicity: An American Girl Adventure'', a 2005 TV movie Other uses * Felicity (given name), a list of people and fictional characters * Felicity (pragmatics), a term used in formal semantics and pragmatics * Felicity Party, an Islamist Turkish political party founded in 2001 * Felicity Plantation, a historic sugar plantation in Louisiana, United States * , a Royal Navy Second World War minesweeper * ''Felicity'', an 18th-century British privateer which captured See also * Felicitas (other) * Santa Felicita di Firenze, the second-oldest church in Florence * The 1982 single "Felicità "Felicità" (; Italian for "Happiness") is a song by Ita ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utility Function
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosophers such as Jeremy Bentham and John Stuart Mill. The term has been adapted and reapplied within neoclassical economics, which dominates modern economic theory, as a utility function that represents a single consumer's preference ordering over a choice set but is not comparable across consumers. This concept of utility is personal and based on choice rather than on pleasure received, and so is specified more rigorously than the original concept but makes it less useful (and controversial) for ethical decisions. Utility function Consider a set of alternatives among which a person can make a preference ordering. The utility obtained from these alternatives is an unknown function of the utilities obtained from each alternative, not the sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Discounting
In economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time (with or without uncertainty). Formally, exponential discounting occurs when total utility is given by :U(\_^)=\sum_^\delta^(u(c_t)), where ''c''''t'' is consumption at time ''t'', \delta is the exponential discount factor, and ''u'' is the instantaneous utility function. In continuous time, exponential discounting is given by :U(\_^)=\int_^ e^u(c(t))\,dt, Exponential discounting implies that the marginal rate of substitution between consumption at any pair of points in time depends only on how far apart those two points are. Exponential discounting is not dynamically inconsistent. A key aspect of the exponential discounting assumption is the property of dynamic consistency— preferences are constant over time. In other words, preferences do not change with the passage of time unless new information is presented. For example, consider an investment op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economics
Economics () is the social science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interactions of Agent (economics), economic agents and how economy, economies work. Microeconomics analyzes what's viewed as basic elements in the economy, including individual agents and market (economics), markets, their interactions, and the outcomes of interactions. Individual agents may include, for example, households, firms, buyers, and sellers. Macroeconomics analyzes the economy as a system where production, consumption, saving, and investment interact, and factors affecting it: employment of the resources of labour, capital, and land, currency inflation, economic growth, and public policies that have impact on glossary of economics, these elements. Other broad distinctions within economics include those between positive economics, desc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Optimization Theory And Applications
A journal, from the Old French ''journal'' (meaning "daily"), may refer to: *Bullet journal, a method of personal organization *Diary, a record of what happened over the course of a day or other period *Daybook, also known as a general journal, a daily record of financial transactions *Logbook, a record of events important to the operation of a vehicle, facility, or otherwise *Record (other) *Transaction log, a chronological record of data processing *Travel journal In publishing, ''journal'' can refer to various periodicals or serials: *Academic journal, an academic or scholarly periodical **Scientific journal, an academic journal focusing on science **Medical journal, an academic journal focusing on medicine **Law review, a professional journal focusing on legal interpretation *Magazine, non-academic or scholarly periodicals in general **Trade magazine, a magazine of interest to those of a particular profession or trade **Literary magazine, a magazine devoted to literat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
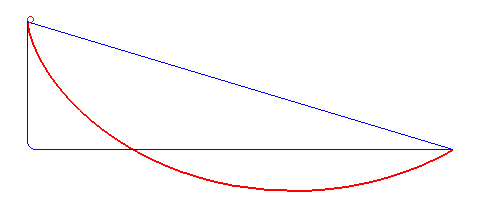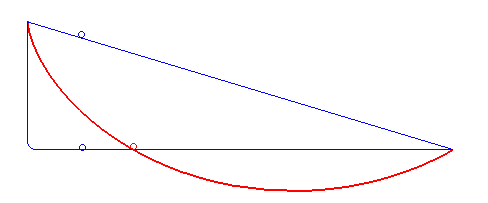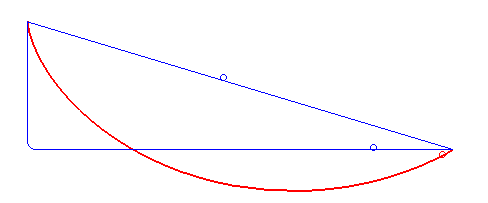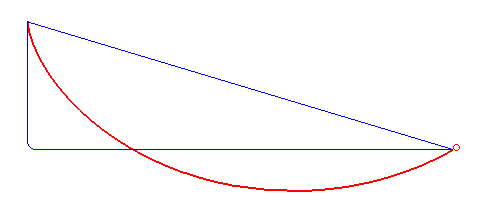
Brachistochrone Problem
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: Thomson Brooks/Cole, 2012. 640. Pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Momentum
In mathematics and classical mechanics, canonical coordinates are sets of coordinates on phase space which can be used to describe a physical system at any given point in time. Canonical coordinates are used in the Hamiltonian formulation of classical mechanics. A closely related concept also appears in quantum mechanics; see the Stone–von Neumann theorem and canonical commutation relations for details. As Hamiltonian mechanics are generalized by symplectic geometry and canonical transformations are generalized by contact transformations, so the 19th century definition of canonical coordinates in classical mechanics may be generalized to a more abstract 20th century definition of coordinates on the cotangent bundle of a manifold (the mathematical notion of phase space). Definition in classical mechanics In classical mechanics, canonical coordinates are coordinates q^i and p_i in phase space that are used in the Hamiltonian formalism. The canonical coordinates satisfy the fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least action). It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his 1788 work, '' Mécanique analytique''. Lagrangian mechanics describes a mechanical system as a pair (M,L) consisting of a configuration space M and a smooth function L within that space called a ''Lagrangian''. By convention, L = T - V, where T and V are the kinetic and potential energy of the system, respectively. The stationary action principle requires that the action functional of the system derived from L must remain at a stationary point (a maximum, minimum, or saddle) throughout the time evolution of the system. This constraint allows the calculation of the equations of motion of the system using Lagrange's equations. Introduction Suppose there exists a bead sliding around on a wire, or a swinging simple p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Rowan Hamilton
Sir William Rowan Hamilton Doctor of Law, LL.D, Doctor of Civil Law, DCL, Royal Irish Academy, MRIA, Royal Astronomical Society#Fellow, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the Andrews Professor of Astronomy at Trinity College Dublin, and Royal Astronomer of Ireland, living at Dunsink Observatory. Hamilton's scientific career included the study of geometrical optics, ideas from Fourier analysis, and his work on quaternions which made him one of the founders of modern linear algebra. He made major contributions in optics, classical mechanics and abstract algebra. His work was fundamental to modern theoretical physics, particularly his reformulation of Newtonian mechanics, now called Hamiltonian mechanics. It is now central both to electromagnetism and to quantum mechanics. Early life Hamilton was the fourth of nine children born to Sarah Hutton (1780–1817) and Archibald Hamilton (1778–1819),Bruno (2003) who ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
