|
Bochner–Kodaira–Nakano Identity
In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ..., the Bochner–Kodaira–Nakano identity is an analogue of the Weitzenböck identity for hermitian manifolds, giving an expression for the antiholomorphic Laplacian of a vector bundle over a hermitian manifold in terms of its complex conjugate and the curvature of the bundle and the torsion of the metric of the manifold. It is named after Salomon Bochner, Kunihiko Kodaira, and Shigeo Nakano. References * * * Theorems in differential geometry Vector bundles Mathematical identities {{differential-geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weitzenböck Identity
In mathematics, in particular in differential geometry, mathematical physics, and representation theory a Weitzenböck identity, named after Roland Weitzenböck, expresses a relationship between two second-order elliptic operators on a manifold with the same principal symbol. Usually Weitzenböck formulae are implemented for ''G''-invariant self-adjoint operators between vector bundles associated to some principal ''G''-bundle, although the precise conditions under which such a formula exists are difficult to formulate. This article focuses on three examples of Weitzenböck identities: from Riemannian geometry, spin geometry, and complex analysis. Riemannian geometry In Riemannian geometry there are two notions of the Laplacian on differential forms over an oriented compact Riemannian manifold ''M''. The first definition uses the divergence operator ''δ'' defined as the formal adjoint of the de Rham operator ''d'': \int_M \langle \alpha,\delta\beta\rangle := \int_M\langle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Manifold
In mathematics, and more specifically in differential geometry, a Hermitian manifold is the complex analogue of a Riemannian manifold. More precisely, a Hermitian manifold is a complex manifold with a smoothly varying Hermitian inner product on each (holomorphic) tangent space. One can also define a Hermitian manifold as a real manifold with a Riemannian metric that preserves a complex structure. A complex structure is essentially an almost complex structure with an integrability condition, and this condition yields a unitary structure ( U(n) structure) on the manifold. By dropping this condition, we get an almost Hermitian manifold. On any almost Hermitian manifold, we can introduce a fundamental 2-form (or cosymplectic structure) that depends only on the chosen metric and the almost complex structure. This form is always non-degenerate. With the extra integrability condition that it is closed (i.e., it is a symplectic form), we get an almost Kähler structure. If both the al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiholomorphic Function
In mathematics, antiholomorphic functions (also called antianalytic functionsEncyclopedia of Mathematics, Springer and The European Mathematical Society, https://encyclopediaofmath.org/wiki/Anti-holomorphic_function, As of 11 September 2020, This article was adapted from an original article by E. D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics, .) are a family of functions closely related to but distinct from holomorphic functions. A function of the complex variable z defined on an open set in the complex plane is said to be antiholomorphic if its derivative with respect to exists in the neighbourhood of each and every point in that set, where is the complex conjugate. A definition of antiholomorphic function follows: " function f (z) = u + i v of one or more complex variables z = \left(z_1, \dots, z_n\right) \in \Complex^n s said to be anti-holomorphic if (and only if) itis the complex conjugate of a holomorphic function \overline = u - i v." One ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
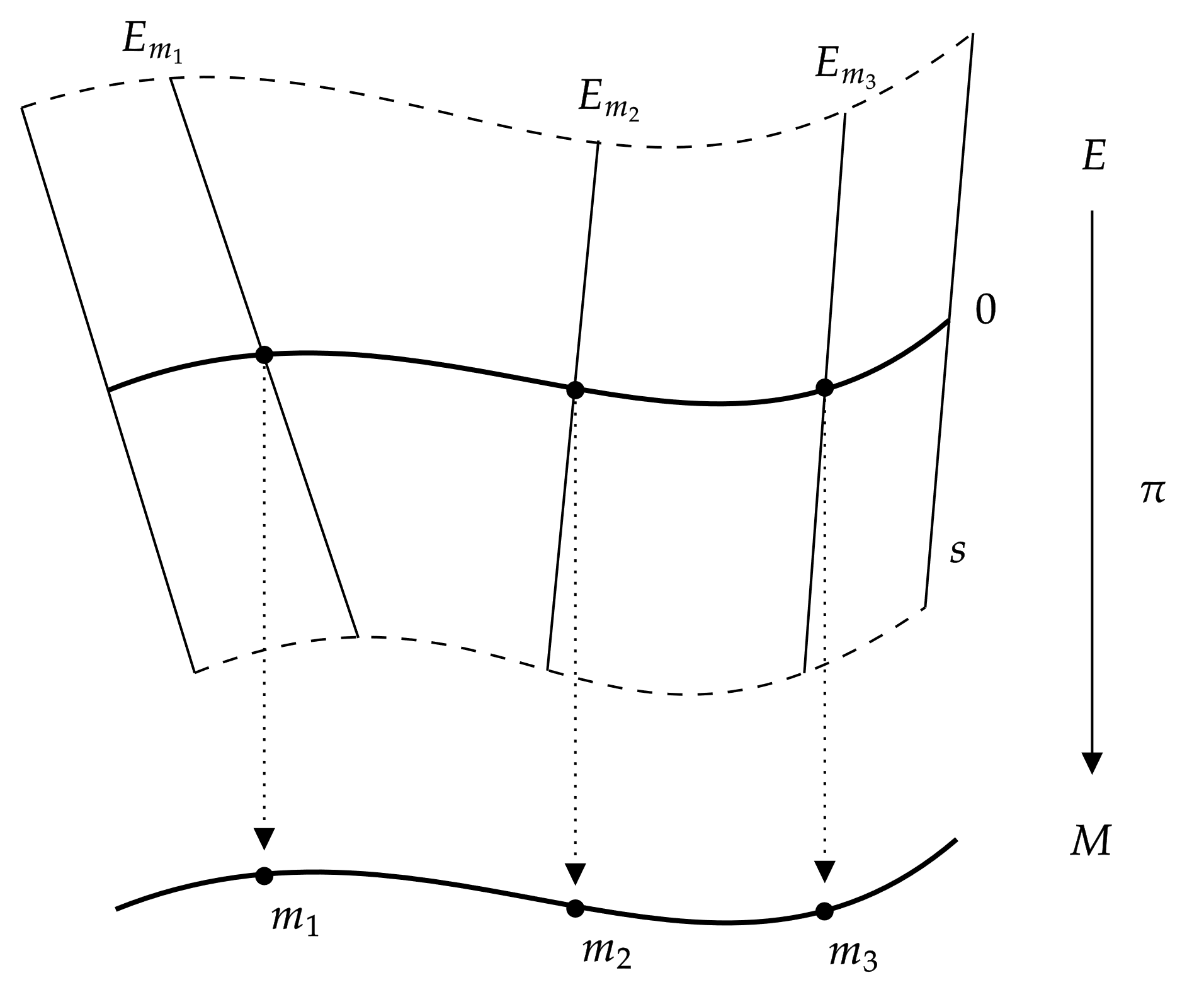
Vector Bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X. The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x)=V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X\times V over X. Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Salomon Bochner
Salomon Bochner (20 August 1899 – 2 May 1982) was an Austrian mathematician, known for work in mathematical analysis, probability theory and differential geometry. Life He was born into a Jewish family in Podgórze (near Kraków), then Austria-Hungary, now Poland. Fearful of a Russian invasion in Galicia at the beginning of World War I in 1914, his family moved to Germany, seeking greater security. Bochner was educated at a Berlin gymnasium (secondary school), and then at the University of Berlin. There, he was a student of Erhard Schmidt, writing a dissertation involving what would later be called the Bergman kernel. Shortly after this, he left the academy to help his family during the escalating inflation. After returning to mathematical research, he lectured at the University of Munich from 1924 to 1933. His academic career in Germany ended after the Nazis came to power in 1933, and he left for a position at Princeton University. He was a visiting scholar at the Inst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kunihiko Kodaira
was a Japanese mathematician known for distinguished work in algebraic geometry and the theory of complex manifolds, and as the founder of the Japanese school of algebraic geometers. He was awarded a Fields Medal in 1954, being the first Japanese national to receive this honour. Early years Kodaira was born in Tokyo. He graduated from the University of Tokyo in 1938 with a degree in mathematics and also graduated from the physics department at the University of Tokyo in 1941. During the war years he worked in isolation, but was able to master Hodge theory as it then stood. He obtained his PhD from the University of Tokyo in 1949, with a thesis entitled ''Harmonic fields in Riemannian manifolds''. He was involved in cryptographic work from about 1944, while holding an academic post in Tokyo. Institute for Advanced Study and Princeton University In 1949 he travelled to the Institute for Advanced Study in Princeton, New Jersey at the invitation of Hermann Weyl. He was subseq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shigeo Nakano
Shigeo (written: 茂雄, 茂生, 茂男, 茂夫, 成雄, 成男, 重雄, 重男, 重夫, 繁雄, 繁男, 晟郎, 殖生 or 滋雄) is a masculine Japanese given name. Notable people with the name include: *, Japanese photographer *, Japanese swimmer *, Japanese sculptor and graphic designer *, Japanese swimmer *, Japanese photographer *, Japanese photographer *, Japanese inventor and academic *, Japanese table tennis player *, Japanese musicologist *, Japanese politician *, Japanese actor *, Japanese botanist *, Japanese businessman *, Japanese engineer *, Japanese sumo wrestler *, Japanese baseball player and manager *, Japanese swimmer *, Japanese boxer *, Japanese sport wrestler *, Japanese footballer *, Japanese professional wrestler *, Japanese politician *, Japanese footballer *, Japanese mathematician *, Japanese physicist *, Japanese footballer and manager *, Japanese engineer *, Japanese footballer *, Japanese swimmer *, Japanese mayor *, Japanese judge *, Japanese AV actor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proceedings Of The National Academy Of Sciences
''Proceedings of the National Academy of Sciences of the United States of America'' (often abbreviated ''PNAS'' or ''PNAS USA'') is a peer-reviewed multidisciplinary scientific journal. It is the official journal of the National Academy of Sciences, published since 1915, and publishes original research, scientific reviews, commentaries, and letters. According to ''Journal Citation Reports'', the journal has a 2021 impact factor of 12.779. ''PNAS'' is the second most cited scientific journal, with more than 1.9 million cumulative citations from 2008 to 2018. In the mass media, ''PNAS'' has been described variously as "prestigious", "sedate", "renowned" and "high impact". ''PNAS'' is a delayed open access journal, with an embargo period of six months that can be bypassed for an author fee ( hybrid open access). Since September 2017, open access articles are published under a Creative Commons license. Since January 2019, ''PNAS'' has been online-only, although print issues are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theorems In Differential Geometry
In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems. In the mainstream of mathematics, the axioms and the inference rules are commonly left implicit, and, in this case, they are almost always those of Zermelo–Fraenkel set theory with the axiom of choice, or of a less powerful theory, such as Peano arithmetic. A notable exception is Wiles's proof of Fermat's Last Theorem, which involves the Grothendieck universes whose existence requires the addition of a new axiom to the set theory. Generally, an assertion that is explicitly called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as ''theorems'' only the most important results, and use the terms ''lemma'', ''proposition'' and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Bundles
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X. The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x)=V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X\times V over X. Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a manifold ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |