Vector bundles on:
[Wikipedia]
[Google]
[Amazon]
 In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of
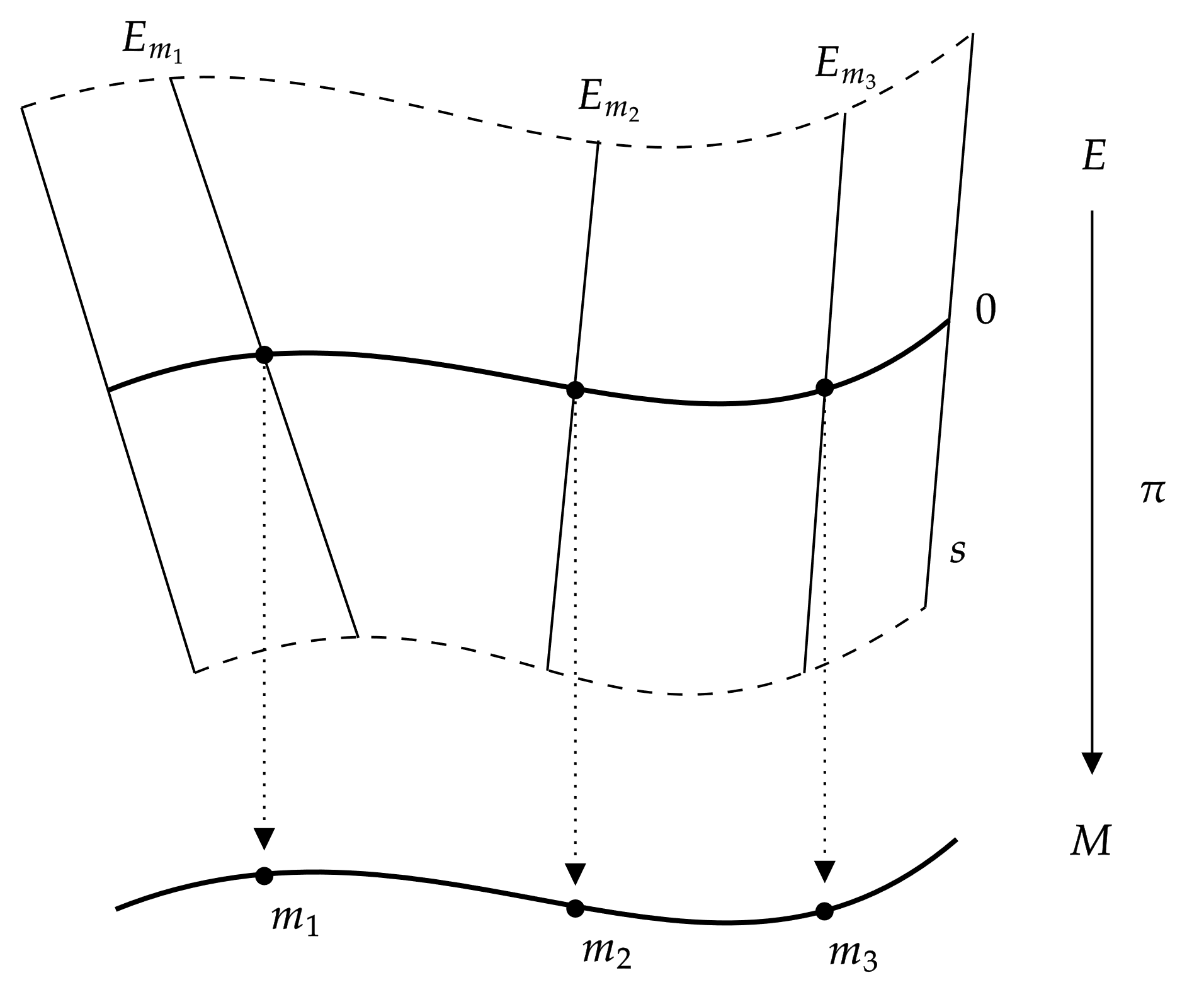 A real vector bundle consists of:
# topological spaces (''base space'') and (''total space'')
# a continuous
A real vector bundle consists of:
# topological spaces (''base space'') and (''total space'')
# a continuous
 Given a vector bundle of rank , and a pair of neighborhoods and over which the bundle trivializes via
:
the composite function
:
is well-defined on the overlap, and satisfies
:
for some -valued function
:
These are called the transition functions (or the coordinate transformations) of the vector bundle.
The set of transition functions forms a Δech cocycle in the sense that
:
for all over which the bundle trivializes satisfying . Thus the data defines a
Given a vector bundle of rank , and a pair of neighborhoods and over which the bundle trivializes via
:
the composite function
:
is well-defined on the overlap, and satisfies
:
for some -valued function
:
These are called the transition functions (or the coordinate transformations) of the vector bundle.
The set of transition functions forms a Δech cocycle in the sense that
:
for all over which the bundle trivializes satisfying . Thus the data defines a
 One simple method of constructing vector bundles is by taking subbundles of other vector bundles. Given a vector bundle over a topological space, a subbundle is simply a subspace for which the restriction of to gives the structure of a vector bundle also. In this case the fibre is a vector subspace for every .
A subbundle of a trivial bundle need not be trivial, and indeed every real vector bundle can be viewed as a subbundle of a trivial bundle of sufficiently high rank. For example the MΓΆbius band, a non-trivial line bundle over the circle, can be seen as a subbundle of the trivial rank 2 bundle over the circle.
One simple method of constructing vector bundles is by taking subbundles of other vector bundles. Given a vector bundle over a topological space, a subbundle is simply a subspace for which the restriction of to gives the structure of a vector bundle also. In this case the fibre is a vector subspace for every .
A subbundle of a trivial bundle need not be trivial, and indeed every real vector bundle can be viewed as a subbundle of a trivial bundle of sufficiently high rank. For example the MΓΆbius band, a non-trivial line bundle over the circle, can be seen as a subbundle of the trivial rank 2 bundle over the circle.
Why is it useful to study vector bundles ?
on MathOverflow
Why is it useful to classify the vector bundles of a space ?
{{Manifolds
vector space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called '' vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but ...
s parameterized by another space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. In classical physics, physical space is often conceived in three linear dimensions, although modern physicists usually con ...
(for example could be a topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called po ...
, a manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a ...
, or an algebraic variety
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers ...
): to every point of the space we associate (or "attach") a vector space in such a way that these vector spaces fit together to form another space of the same kind as (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over .
The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space such that for all in : in this case there is a copy of for each in and these copies fit together to form the vector bundle over . Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is a manifold TM which assembles all the tangent vectors in M . As a set, it is given by the disjoint unionThe disjoint union ensures that for any two points and ...
s of smooth (or differentiable) manifolds: to every point of such a manifold we attach the tangent space to the manifold at that point. Tangent bundles are not, in general, trivial bundles. For example, the tangent bundle of the sphere is non-trivial by the hairy ball theorem
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous tangent vector field on even-dimensional ''n''-spheres. For the ordinary sphere, or 2βsphere, ...
. In general, a manifold is said to be parallelizable if, and only if, its tangent bundle is trivial.
Vector bundles are almost always required to be ''locally trivial'', however, which means they are examples of fiber bundle
In mathematics, and particularly topology, a fiber bundle (or, in Commonwealth English: fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a ...
s. Also, the vector spaces are usually required to be over the real or complex numbers, in which case the vector bundle is said to be a real or complex vector bundle (respectively). Complex vector bundles can be viewed as real vector bundles with additional structure. In the following, we focus on real vector bundles in the category of topological spaces In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again con ...
.
Definition and first consequences
 A real vector bundle consists of:
# topological spaces (''base space'') and (''total space'')
# a continuous
A real vector bundle consists of:
# topological spaces (''base space'') and (''total space'')
# a continuous surjection
In mathematics, a surjective function (also known as surjection, or onto function) is a function that every element can be mapped from element so that . In other words, every element of the function's codomain is the image of one element of ...
(''bundle projection'')
# for every in , the structure of a finite-dimensional real vector space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called '' vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but ...
on the fiber
Fiber or fibre (from la, fibra, links=no) is a natural or artificial substance that is significantly longer than it is wide. Fibers are often used in the manufacture of other materials. The strongest engineering materials often incorpora ...
where the following compatibility condition is satisfied: for every point in , there is an open neighborhood of , a natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called '' cardinal ...
, and a homeomorphism
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomor ...
:
such that for all in ,
* for all vectors in , and
* the map is a linear isomorphism between the vector spaces and .
The open neighborhood together with the homeomorphism is called a local trivialization of the vector bundle. The local trivialization shows that ''locally'' the map "looks like" the projection of on .
Every fiber is a finite-dimensional real vector space and hence has a dimension . The local trivializations show that the function is locally constant, and is therefore constant on each connected component of . If is equal to a constant on all of , then is called the rank of the vector bundle, and is said to be a vector bundle of rank . Often the definition of a vector bundle includes that the rank is well defined, so that is constant. Vector bundles of rank 1 are called line bundles, while those of rank 2 are less commonly called plane bundles.
The Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''Γ''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is
: A\ ...
, equipped with the projection , is called the trivial bundle of rank over .
Transition functions
 Given a vector bundle of rank , and a pair of neighborhoods and over which the bundle trivializes via
:
the composite function
:
is well-defined on the overlap, and satisfies
:
for some -valued function
:
These are called the transition functions (or the coordinate transformations) of the vector bundle.
The set of transition functions forms a Δech cocycle in the sense that
:
for all over which the bundle trivializes satisfying . Thus the data defines a
Given a vector bundle of rank , and a pair of neighborhoods and over which the bundle trivializes via
:
the composite function
:
is well-defined on the overlap, and satisfies
:
for some -valued function
:
These are called the transition functions (or the coordinate transformations) of the vector bundle.
The set of transition functions forms a Δech cocycle in the sense that
:
for all over which the bundle trivializes satisfying . Thus the data defines a fiber bundle
In mathematics, and particularly topology, a fiber bundle (or, in Commonwealth English: fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a ...
; the additional data of the specifies a structure group in which the action on the fiber is the standard action of .
Conversely, given a fiber bundle with a cocycle acting in the standard way on the fiber , there is associated a vector bundle. This is an example of the fibre bundle construction theorem for vector bundles, and can be taken as an alternative definition of a vector bundle.
Subbundles
 One simple method of constructing vector bundles is by taking subbundles of other vector bundles. Given a vector bundle over a topological space, a subbundle is simply a subspace for which the restriction of to gives the structure of a vector bundle also. In this case the fibre is a vector subspace for every .
A subbundle of a trivial bundle need not be trivial, and indeed every real vector bundle can be viewed as a subbundle of a trivial bundle of sufficiently high rank. For example the MΓΆbius band, a non-trivial line bundle over the circle, can be seen as a subbundle of the trivial rank 2 bundle over the circle.
One simple method of constructing vector bundles is by taking subbundles of other vector bundles. Given a vector bundle over a topological space, a subbundle is simply a subspace for which the restriction of to gives the structure of a vector bundle also. In this case the fibre is a vector subspace for every .
A subbundle of a trivial bundle need not be trivial, and indeed every real vector bundle can be viewed as a subbundle of a trivial bundle of sufficiently high rank. For example the MΓΆbius band, a non-trivial line bundle over the circle, can be seen as a subbundle of the trivial rank 2 bundle over the circle.
Vector bundle morphisms
A morphism from the vector bundle 1: ''E''1 β ''X''1 to the vector bundle 2: ''E''2 β ''X''2 is given by a pair of continuous maps ''f'': ''E''1 β ''E''2 and ''g'': ''X''1 β ''X''2 such that : ''g'' β 1 = 2 β ''f'' :: : for every ''x'' in ''X''1, the map 1β1() β 2β1() induced by ''f'' is a linear map between vector spaces. Note that ''g'' is determined by ''f'' (because 1 is surjective), and ''f'' is then said to cover ''g''. The class of all vector bundles together with bundle morphisms forms acategory
Category, plural categories, may refer to:
Philosophy and general uses
*Categorization, categories in cognitive science, information science and generally
* Category of being
* ''Categories'' (Aristotle)
* Category (Kant)
* Categories (Peirce) ...
. Restricting to vector bundles for which the spaces are manifolds (and the bundle projections are smooth maps) and smooth bundle morphisms we obtain the category of smooth vector bundles. Vector bundle morphisms are a special case of the notion of a bundle map between fiber bundle
In mathematics, and particularly topology, a fiber bundle (or, in Commonwealth English: fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a ...
s, and are sometimes called (vector) bundle homomorphisms.
A bundle homomorphism from ''E''1 to ''E''2 with an inverse which is also a bundle homomorphism (from ''E''2 to ''E''1) is called a (vector) bundle isomorphism, and then ''E''1 and ''E''2 are said to be isomorphic vector bundles. An isomorphism of a (rank ''k'') vector bundle ''E'' over ''X'' with the trivial bundle (of rank ''k'' over ''X'') is called a trivialization of ''E'', and ''E'' is then said to be trivial (or trivializable). The definition of a vector bundle shows that any vector bundle is locally trivial.
We can also consider the category of all vector bundles over a fixed base space ''X''. As morphisms in this category we take those morphisms of vector bundles whose map on the base space is the identity map on ''X''. That is, bundle morphisms for which the following diagram commutes:
:
(Note that this category is ''not'' abelian
Abelian may refer to:
Mathematics Group theory
* Abelian group, a group in which the binary operation is commutative
** Category of abelian groups (Ab), has abelian groups as objects and group homomorphisms as morphisms
* Metabelian group, a grou ...
; the kernel
Kernel may refer to:
Computing
* Kernel (operating system), the central component of most operating systems
* Kernel (image processing), a matrix used for image convolution
* Compute kernel, in GPGPU programming
* Kernel method, in machine lea ...
of a morphism of vector bundles is in general not a vector bundle in any natural way.)
A vector bundle morphism between vector bundles 1: ''E''1 β ''X''1 and 2: ''E''2 β ''X''2 covering a map ''g'' from ''X''1 to ''X''2 can also be viewed as a vector bundle morphism over ''X''1 from ''E''1 to the pullback bundle ''g''*''E''2.
Sections and locally free sheaves
Given a vector bundle : ''E'' β ''X'' and an open subset ''U'' of ''X'', we can consider sections of on ''U'', i.e. continuous functions ''s'': ''U'' β ''E'' where the composite β ''s'' is such that for all ''u'' in ''U''. Essentially, a section assigns to every point of ''U'' a vector from the attached vector space, in a continuous manner. As an example, sections of the tangent bundle of a differential manifold are nothing but vector fields on that manifold. Let ''F''(''U'') be the set of all sections on ''U''. ''F''(''U'') always contains at least one element, namely the zero section: the function ''s'' that maps every element ''x'' of ''U'' to the zero element of the vector space β1(). With the pointwise addition and scalar multiplication of sections, ''F''(''U'') becomes itself a real vector space. The collection of these vector spaces is a sheaf of vector spaces on ''X''. If ''s'' is an element of ''F''(''U'') and Ξ±: ''U'' β R is a continuous map, then Ξ±''s'' (pointwise scalar multiplication) is in ''F''(''U''). We see that ''F''(''U'') is a module over the ring of continuous real-valued functions on ''U''. Furthermore, if O''X'' denotes the structure sheaf of continuous real-valued functions on ''X'', then ''F'' becomes a sheaf of O''X''-modules. Not every sheaf of O''X''-modules arises in this fashion from a vector bundle: only the locally free ones do. (The reason: locally we are looking for sections of a projection ''U'' Γ R''k'' β ''U''; these are precisely the continuous functions ''U'' β R''k'', and such a function is a ''k''-tuple of continuous functions ''U'' β R.) Even more: the category of real vector bundles on ''X'' is equivalent to the category of locally free and finitely generated sheaves of O''X''-modules. So we can think of the category of real vector bundles on ''X'' as sitting inside the category of sheaves of O''X''-modules; this latter category is abelian, so this is where we can compute kernels and cokernels of morphisms of vector bundles. A rank ''n'' vector bundle is trivial if and only if it has ''n'' linearly independent global sections.Operations on vector bundles
Most operations on vector spaces can be extended to vector bundles by performing the vector space operation ''fiberwise''. For example, if ''E'' is a vector bundle over ''X'', then there is a bundle ''E*'' over ''X'', called the dual bundle, whose fiber at ''x'' β ''X'' is thedual vector space
In mathematics, any vector space ''V'' has a corresponding dual vector space (or just dual space for short) consisting of all linear forms on ''V'', together with the vector space structure of pointwise addition and scalar multiplication by con ...
(''Ex'')*. Formally ''E*'' can be defined as the set of pairs (''x'', Ο), where ''x'' β ''X'' and Ο β (''E''''x'')*. The dual bundle is locally trivial because the dual space
In mathematics, any vector space ''V'' has a corresponding dual vector space (or just dual space for short) consisting of all linear forms on ''V'', together with the vector space structure of pointwise addition and scalar multiplication by con ...
of the inverse of a local trivialization of ''E'' is a local trivialization of ''E*'': the key point here is that the operation of taking the dual vector space is functorial.
There are many functorial operations which can be performed on pairs of vector spaces (over the same field), and these extend straightforwardly to pairs of vector bundles ''E'', ''F'' on ''X'' (over the given field). A few examples follow.
* The Whitney sum (named for Hassler Whitney
Hassler Whitney (March 23, 1907 β May 10, 1989) was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, characteristic classes, and geometric integrati ...
) or direct sum bundle of ''E'' and ''F'' is a vector bundle ''E'' β ''F'' over ''X'' whose fiber over ''x'' is the direct sum
The direct sum is an operation between structures in abstract algebra, a branch of mathematics. It is defined differently, but analogously, for different kinds of structures. To see how the direct sum is used in abstract algebra, consider a mo ...
''Ex'' β ''Fx'' of the vector spaces ''Ex'' and ''Fx''.
* The tensor product bundle ''E'' β ''F'' is defined in a similar way, using fiberwise tensor product
In mathematics, the tensor product V \otimes W of two vector spaces and (over the same Field (mathematics), field) is a vector space to which is associated a bilinear map V\times W \to V\otimes W that maps a pair (v,w),\ v\in V, w\in W to an e ...
of vector spaces.
* The Hom-bundle Hom(''E'', ''F'') is a vector bundle whose fiber at ''x'' is the space of linear maps from ''Ex'' to ''Fx'' (which is often denoted Hom(''E''''x'', ''Fx'') or ''L''(''E''''x'', ''F''''x'')). The Hom-bundle is so-called (and useful) because there is a bijection between vector bundle homomorphisms from ''E'' to ''F'' over ''X'' and sections of Hom(''E'', ''F'') over ''X''.
* Building on the previous example, given a section ''s'' of an endomorphism bundle Hom(''E'', ''E'') and a function ''f'': ''X'' β R, one can construct an eigenbundle by taking the fiber over a point ''x'' β ''X'' to be the ''f''(''x'')- eigenspace of the linear map ''s''(''x''): ''E''''x'' β ''E''''x''. Though this construction is natural, unless care is taken, the resulting object will not have local trivializations. Consider the case of ''s'' being the zero section and ''f'' having isolated zeroes. The fiber over these zeroes in the resulting "eigenbundle" will be isomorphic to the fiber over them in ''E'', while everywhere else the fiber is the trivial 0-dimensional vector space.
* The dual vector bundle In mathematics, the dual bundle is an operation on vector bundles extending the operation of duality for vector spaces.
Definition
The dual bundle of a vector bundle \pi: E \to X is the vector bundle \pi^*: E^* \to X whose fibers are the dual sp ...
''E*'' is the Hom bundle Hom(''E'', R Γ ''X'') of bundle homomorphisms of ''E'' and the trivial bundle R Γ ''X''. There is a canonical vector bundle isomorphism Hom(''E'', ''F'') = ''E*'' β ''F''.
Each of these operations is a particular example of a general feature of bundles: that many operations that can be performed on the category of vector spaces can also be performed on the category of vector bundles in a functor
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects (such as the fundamental group) are associated to topological spaces, an ...
ial manner. This is made precise in the language of smooth functors. An operation of a different nature is the pullback bundle construction. Given a vector bundle ''E'' β ''Y'' and a continuous map ''f'': ''X'' β ''Y'' one can "pull back" ''E'' to a vector bundle ''f*E'' over ''X''. The fiber over a point ''x'' β ''X'' is essentially just the fiber over ''f''(''x'') β ''Y''. Hence, Whitney summing ''E'' β ''F'' can be defined as the pullback bundle of the diagonal map from ''X'' to ''X'' Γ ''X'' where the bundle over ''X'' Γ ''X'' is ''E'' Γ ''F''.
Remark: Let ''X'' be a compact space. Any vector bundle ''E'' over ''X'' is a direct summand of a trivial bundle; i.e., there exists a bundle ''E'' such that ''E'' β ''E'' is trivial. This fails if ''X'' is not compact: for example, the tautological line bundle In mathematics, the tautological bundle is a vector bundle occurring over a Grassmannian in a natural tautological way: for a Grassmannian of k-dimensional subspaces of V, given a point in the Grassmannian corresponding to a k-dimensional vector ...
over the infinite real projective space does not have this property.
Additional structures and generalizations
Vector bundles are often given more structure. For instance, vector bundles may be equipped with a vector bundle metric. Usually this metric is required to be positive definite, in which case each fibre of ''E'' becomes a Euclidean space. A vector bundle with a complex structure corresponds to a complex vector bundle, which may also be obtained by replacing real vector spaces in the definition with complex ones and requiring that all mappings be complex-linear in the fibers. More generally, one can typically understand the additional structure imposed on a vector bundle in terms of the resulting reduction of the structure group of a bundle. Vector bundles over more general topological fields may also be used. If instead of a finite-dimensional vector space, if the fiber ''F'' is taken to be aBanach space
In mathematics, more specifically in functional analysis, a Banach space (pronounced ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between ve ...
then a Banach bundle is obtained. Specifically, one must require that the local trivializations are Banach space isomorphisms (rather than just linear isomorphisms) on each of the fibers and that, furthermore, the transitions
:
are continuous mappings of Banach manifolds. In the corresponding theory for C''p'' bundles, all mappings are required to be C''p''.
Vector bundles are special fiber bundle
In mathematics, and particularly topology, a fiber bundle (or, in Commonwealth English: fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a ...
s, those whose fibers are vector spaces and whose cocycle respects the vector space structure. More general fiber bundles can be constructed in which the fiber may have other structures; for example sphere bundle In the mathematical field of topology, a sphere bundle is a fiber bundle in which the fibers are spheres S^n of some dimension ''n''. Similarly, in a disk bundle, the fibers are disks D^n. From a topological perspective, there is no difference betw ...
s are fibered by spheres.
Smooth vector bundles
A vector bundle (''E'', ''p'', ''M'') is smooth, if ''E'' and ''M'' are smooth manifolds, p: ''E'' β ''M'' is a smooth map, and the local trivializations arediffeomorphism
In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are differentiable.
Definition
Given tw ...
s. Depending on the required degree of smoothness, there are different corresponding notions of ''Cp'' bundles, infinitely differentiable ''C''β-bundles and real analytic ''C''Ο-bundles. In this section we will concentrate on ''C''β-bundles. The most important example of a ''C''β-vector bundle is the tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is a manifold TM which assembles all the tangent vectors in M . As a set, it is given by the disjoint unionThe disjoint union ensures that for any two points and ...
(''TM'', ''TM'', ''M'') of a ''C''β-manifold ''M''.
A smooth vector bundle can be characterized by the fact that it admits transition functions as described above which are ''smooth'' functions on overlaps of trivializing charts ''U'' and ''V''. That is, a vector bundle ''E'' is smooth if it admits a covering by trivializing open sets such that for any two such sets ''U'' and ''V'', the transition function
:
is a smooth function into the matrix group GL(k,R), which is a Lie group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the addit ...
.
Similarly, if the transition functions are:
* ''Cr'' then the vector bundle is a ''Cr'' vector bundle,
* ''real analytic'' then the vector bundle is a real analytic vector bundle (this requires the matrix group to have a real analytic structure),
* ''holomorphic'' then the vector bundle is a holomorphic vector bundle (this requires the matrix group to be a complex Lie group
In geometry, a complex Lie group is a Lie group over the complex numbers; i.e., it is a complex-analytic manifold that is also a group in such a way G \times G \to G, (x, y) \mapsto x y^ is holomorphic. Basic examples are \operatorname_n(\ma ...
),
* ''algebraic functions'' then the vector bundle is an algebraic vector bundle (this requires the matrix group to be an algebraic group
In mathematics, an algebraic group is an algebraic variety endowed with a group structure which is compatible with its structure as an algebraic variety. Thus the study of algebraic groups belongs both to algebraic geometry and group theory.
...
).
The ''C''β-vector bundles (''E'', ''p'', ''M'') have a very important property not shared by more general ''C''β-fibre bundles. Namely, the tangent space ''Tv''(''E''''x'') at any ''v'' β ''E''''x'' can be naturally identified with the fibre ''E''''x'' itself. This identification is obtained through the ''vertical lift'' ''vl''''v'': ''Ex'' β ''T''''v''(''E''''x''), defined as
:
The vertical lift can also be seen as a natural ''C''β-vector bundle isomorphism ''p*E'' β ''VE'', where (''p*E'', ''p*p'', ''E'') is the pull-back bundle of (''E'', ''p'', ''M'') over ''E'' through ''p'': ''E'' β ''M'', and ''VE'' := Ker(''p''*) β ''TE'' is the ''vertical tangent bundle'', a natural vector subbundle of the tangent bundle (''TE'', ''TE'', ''E'') of the total space ''E''.
The total space ''E'' of any smooth vector bundle carries a natural vector field ''V''''v'' := vl''v''''v'', known as the ''canonical vector field''. More formally, ''V'' is a smooth section of (''TE'', ''TE'', ''E''), and it can also be defined as the infinitesimal generator of the Lie-group action given by the fibrewise scalar multiplication. The canonical vector field ''V'' characterizes completely the smooth vector bundle structure in the following manner. As a preparation, note that when ''X'' is a smooth vector field on a smooth manifold ''M'' and ''x'' β ''M'' such that ''X''''x'' = 0, the linear mapping
:
does not depend on the choice of the linear covariant derivative β on ''M''. The canonical vector field ''V'' on ''E'' satisfies the axioms
# The flow (''t'', ''v'') β Ξ¦''t''''V''(''v'') of ''V'' is globally defined.
# For each ''v'' β ''V'' there is a unique limtββ Ξ¦''t''''V''(''v'') β ''V''.
# ''C''v(''V'')β''C''v(''V'') = ''C''v(''V'') whenever ''V''''v'' = 0.
# The zero set of ''V'' is a smooth submanifold of ''E'' whose codimension is equal to the rank of ''C''v(''V'').
Conversely, if ''E'' is any smooth manifold and ''V'' is a smooth vector field on ''E'' satisfying 1β4, then there is a unique vector bundle structure on ''E'' whose canonical vector field is ''V''.
For any smooth vector bundle (''E'', ''p'', ''M'') the total space ''TE'' of its tangent bundle (''TE'', ''TE'', ''E'') has a natural secondary vector bundle structure (''TE'', ''p''*, ''TM''), where ''p''* is the push-forward of the canonical projection ''p'': ''E'' β ''M''. The vector bundle operations in this secondary vector bundle structure are the push-forwards +*: ''T''(''E'' Γ ''E'') β ''TE'' and Ξ»*: ''TE'' β ''TE'' of the original addition +: ''E'' Γ ''E'' β ''E'' and scalar multiplication Ξ»: ''E'' β ''E''.
K-theory
The K-theory group, , of a compact Hausdorff topological space is defined as the abelian group generated by isomorphism classes of complex vector bundles modulo the relation that whenever we have anexact sequence
An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next.
Definition
In the conte ...
:
then
:
in topological K-theory. KO-theory
In mathematics, topological -theory is a branch of algebraic topology. It was founded to study vector bundles on topological spaces, by means of ideas now recognised as (general) K-theory that were introduced by Alexander Grothendieck. The early ...
is a version of this construction which considers real vector bundles. K-theory with compact support
In mathematics, the support of a real-valued function f is the subset of the function domain containing the elements which are not mapped to zero. If the domain of f is a topological space, then the support of f is instead defined as the smal ...
s can also be defined, as well as higher K-theory groups.
The famous periodicity theorem of Raoul Bott asserts that the K-theory of any space is isomorphic to that of the , the double suspension of .
In algebraic geometry, one considers the K-theory groups consisting of coherent sheaves on a scheme , as well as the K-theory groups of vector bundles on the scheme with the above equivalence relation. The two constructs are the same provided that the underlying scheme is smooth.
See also
General notions
* Grassmannian:classifying space
In mathematics, specifically in homotopy theory, a classifying space ''BG'' of a topological group ''G'' is the quotient of a weakly contractible space ''EG'' (i.e. a topological space all of whose homotopy groups are trivial) by a proper free ac ...
s for vector bundle, among which projective spaces for line bundles
* Characteristic class
* Splitting principle
* Stable bundle In mathematics, a stable vector bundle is a (holomorphic or algebraic) vector bundle that is stable in the sense of geometric invariant theory. Any holomorphic vector bundle may be built from stable ones using HarderβNarasimhan filtration. Stable ...
Topology and differential geometry
*Gauge theory
In physics, a gauge theory is a type of field theory in which the Lagrangian (and hence the dynamics of the system itself) does not change (is invariant) under local transformations according to certain smooth families of operations (Lie groups ...
: the general study of connections on vector bundles and principal bundles and their relations to physics.
* Connection: the notion needed to differentiate sections of vector bundles.
Algebraic and analytic geometry
* Algebraic vector bundle * Picard group * Holomorphic vector bundleNotes
Sources
*. *. *, see section 1.5. *. *. * see Ch.5 *.External links
*Why is it useful to study vector bundles ?
on MathOverflow
Why is it useful to classify the vector bundles of a space ?
{{Manifolds