|
Bitruncation
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
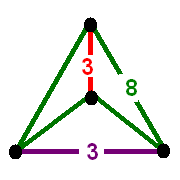
Bitruncated Icosahedral Honeycomb Verf
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that sel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
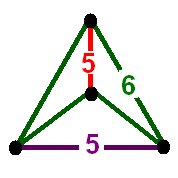
Bitruncated Cubic Honeycomb Verf
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There are two infinite sets of convex prismatic forms, along with 17 cases arising as prisms of the convex uniform polyhedra. There are also an unknown number of non-convex star forms. History of discovery * Convex Regular polytopes: ** 1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 6 regular polytopes in 4 dimensions and only 3 in 5 or more dimensions. * Regular star 4-polytopes (star polyhedron cells and/or vertex figures) ** 1852: Ludwig Schläfli also found 4 of the 10 regular star 4-polytopes, discounting 6 with cells or vertex figures and . ** 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) ''Einleitung in die Leh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncated 5-cell Verf
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncated 24-cell
In geometry, a truncated 24-cell is a uniform 4-polytope (4-dimensional uniform polytope) formed as the truncation of the regular 24-cell. There are two degrees of truncations, including a bitruncation. Truncated 24-cell The truncated 24-cell or truncated icositetrachoron is a uniform 4-dimensional polytope (or uniform 4-polytope), which is bounded by 48 cells: 24 cubes, and 24 truncated octahedra. Each vertex joins three truncated octahedra and one cube, in an equilateral triangular pyramid vertex figure. Construction The truncated 24-cell can be constructed from polytopes with three symmetry groups: *F4 ,4,3 A truncation of the 24-cell. *B4 ,3,4 A cantitruncation of the 16-cell, with two families of truncated octahedral cells. *D4 1,1,1 An omnitruncation of the demitesseract, with three families of truncated octahedral cells. Zonotope It is also a zonotope: it can be formed as the Minkowski sum of the six line segments connecting opposite pairs among the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncated 24-cell Verf
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectification (geometry)
In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope. A rectification operator is sometimes denoted by the letter with a Schläfli symbol. For example, is the rectified cube, also called a cuboctahedron, and also represented as \begin 4 \\ 3 \end. And a rectified cuboctahedron is a rhombicuboctahedron, and also represented as r\begin 4 \\ 3 \end. Conway polyhedron notation uses for ambo as this operator. In graph theory this operation creates a medial graph. The rectification of any regular self-dual polyhedron or tiling will result in another regular polyhedron or tiling with a tiling order of 4, for example the tetrahedron becoming an octahedron As a special case, a square tiling will ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids. Uniform truncation In general any polyhedron (or polytope) can also be truncated with a degree of freedom as to how deep the cut is, as shown in Conway polyhedron notation truncation operation. A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra. In general all single ringed uniform polytopes have a uniform truncation. For example, the icosidodecahedron, represented as Schläfli symbols r or \begin 5 \\ 3 \end, and Coxeter-Dynkin diagram or has a uniform truncation, the truncated icosidodecahedr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncated 5-cell
In geometry, a truncated 5-cell is a uniform 4-polytope (4-dimensional uniform polytope) formed as the truncation of the regular 5-cell. There are two degrees of truncations, including a bitruncation. Truncated 5-cell The truncated 5-cell, truncated pentachoron or truncated 4-simplex is bounded by 10 cells: 5 tetrahedra, and 5 truncated tetrahedra. Each vertex is surrounded by 3 truncated tetrahedra and one tetrahedron; the vertex figure is an elongated tetrahedron. Construction The truncated 5-cell may be constructed from the 5-cell by truncating its vertices at 1/3 of its edge length. This transforms the 5 tetrahedral cells into truncated tetrahedra, and introduces 5 new tetrahedral cells positioned near the original vertices. Structure The truncated tetrahedra are joined to each other at their hexagonal faces, and to the tetrahedra at their triangular faces. Seen in a configuration matrix, all incidence counts between elements are shown. The diagonal f-vector n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron. The truncated octahedron was called the "mecon" by Buckminster Fuller. Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths and . Construction A truncated octahedron is constructed from a regular octahedron with side length 3''a'' by the removal of six right square pyramids, one from each point. These pyramids have both base side length (''a'') and lateral s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Convex Honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells. Twenty-eight such honeycombs are known: * the familiar cubic honeycomb and 7 truncations thereof; * the alternated cubic honeycomb and 4 truncations thereof; * 10 prismatic forms based on the uniform plane tilings (11 if including the cubic honeycomb); * 5 modifications of some of the above by elongation and/or gyration. They can be considered the three-dimensional analogue to the uniform tilings of the plane. The Voronoi diagram of any lattice forms a convex uniform honeycomb in which the cells are zonohedra. History * 1900: Thorold Gosset enumerated the list of semiregular convex polytopes with regular cells (Platonic solids) in his publication ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', including one regular cubic honeycomb, and two semiregular forms with tetrahedra and octahedra. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings or, by extension, to space-filling tessellation with polytope cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. This i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |