|
BIT Predicate
In mathematics and computer science, the BIT predicate, sometimes is a predicate that tests whether the bit of the (starting from the least significant digit) when i is written as a binary number. Its mathematical applications include modeling the membership relation of hereditarily finite sets, and defining the adjacency relation of the Rado graph. In computer science, it is used for efficient representations of set data structures using bit vectors, in defining the private information retrieval problem from communication complexity, and in descriptive complexity theory to formulate logical descriptions of complexity classes. History The BIT predicate was first introduced in 1937 by Wilhelm Ackermann to define the Ackermann coding, which encodes hereditarily finite sets as The BIT predicate can be used to perform membership tests for the encoded sets: \text(i,j) is true if and only if the set encoded is a member of the set encoded Ackermann denoted the predicate \text( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ronald Fagin
Ronald Fagin (born 1945) is an American mathematician and computer scientist, and IBM Fellow at the IBM Almaden Research Center. He is known for his work in database theory, finite model theory, and reasoning about knowledge. Biography Ron Fagin was born and grew up in Oklahoma City, where he attended Northwest Classen High School. He was later elected to the Northwest Classen Hall of Fame. He completed his undergraduate degree at Dartmouth College. Fagin received his Ph.D. in Mathematics from the University of California, Berkeley in 1973, where he worked under the supervision of Robert Vaught. He joined the IBM Research Division in 1973, spending two years at the Thomas J. Watson Research Center, and then transferred in 1975 to what is now the IBM Almaden Research Center in San Jose, California. He has served as program committee chair for ACM Symposium on Principles of Database Systems 1984, Theoretical Aspects of Reasoning about Knowledge 1994, ACM Symposium on Theor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Python (programming Language)
Python is a high-level programming language, high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is type system#DYNAMIC, dynamically type-checked and garbage collection (computer science), garbage-collected. It supports multiple programming paradigms, including structured programming, structured (particularly procedural programming, procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC (programming language), ABC programming language, and he first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000. Python 3.0, released in 2008, was a major revision not completely backward-compatible with earlier versions. Python 2.7.18, released in 2020, was the last release of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Java (programming Language)
Java is a High-level programming language, high-level, General-purpose programming language, general-purpose, Memory safety, memory-safe, object-oriented programming, object-oriented programming language. It is intended to let programmers ''write once, run anywhere'' (Write once, run anywhere, WORA), meaning that compiler, compiled Java code can run on all platforms that support Java without the need to recompile. Java applications are typically compiled to Java bytecode, bytecode that can run on any Java virtual machine (JVM) regardless of the underlying computer architecture. The syntax (programming languages), syntax of Java is similar to C (programming language), C and C++, but has fewer low-level programming language, low-level facilities than either of them. The Java runtime provides dynamic capabilities (such as Reflective programming, reflection and runtime code modification) that are typically not available in traditional compiled languages. Java gained popularity sh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
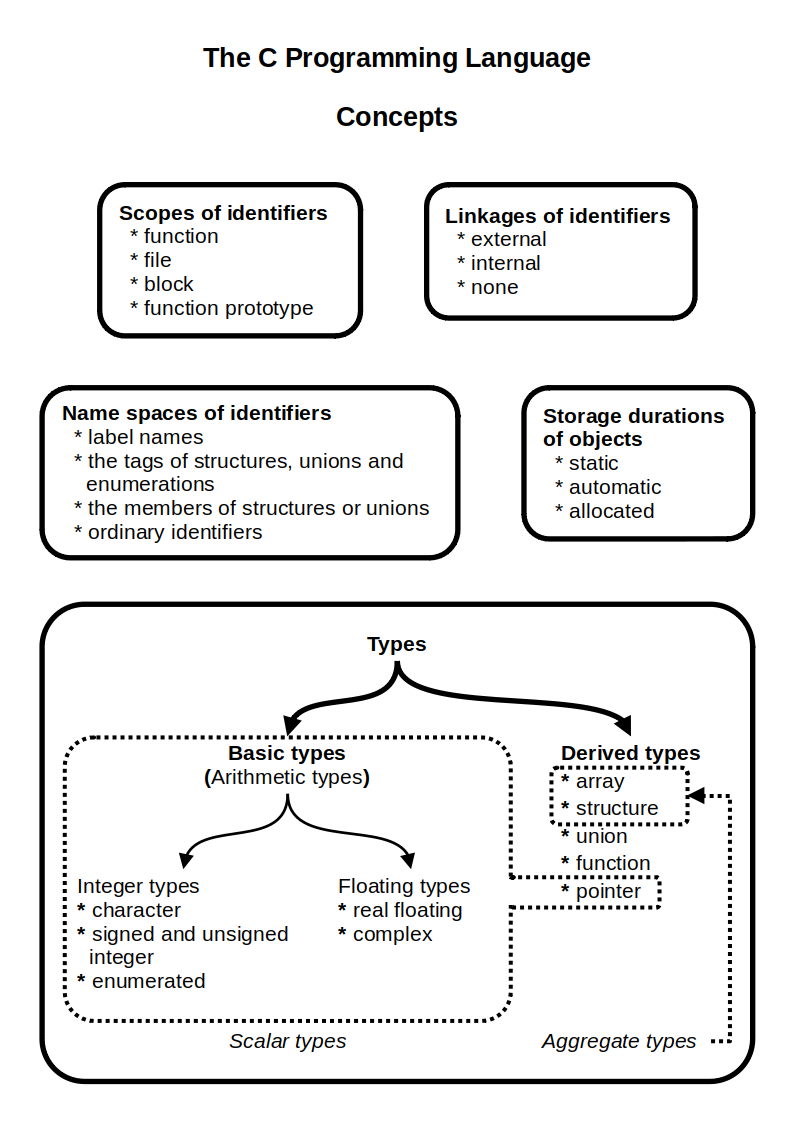
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Asymmetric Relation
In mathematics, an asymmetric relation is a binary relation R on a set X where for all a, b \in X, if a is related to b then b is ''not'' related to a. Formal definition Preliminaries A binary relation on X is any subset R of X \times X. Given a, b \in X, write a R b if and only if (a, b) \in R, which means that a R b is shorthand for (a, b) \in R. The expression a R b is read as "a is related to b by R." Definition The binary relation R is called if for all a, b \in X, if a R b is true then b R a is false; that is, if (a, b) \in R then (b, a) \not\in R. This can be written in the notation of first-order logic as \forall a, b \in X: a R b \implies \lnot(b R a). A logically equivalent definition is: :for all a, b \in X, at least one of a R b and b R a is , which in first-order logic can be written as: \forall a, b \in X: \lnot(a R b \wedge b R a). A relation is asymmetric if and only if it is both antisymmetric and irreflexive, so this may also be taken as a definit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binary Relation
In mathematics, a binary relation associates some elements of one Set (mathematics), set called the ''domain'' with some elements of another set called the ''codomain''. Precisely, a binary relation over sets X and Y is a set of ordered pairs (x, y), where x is an element of X and y is an element of Y. It encodes the common concept of relation: an element x is ''related'' to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. An example of a binary relation is the "divides" relation over the set of prime numbers \mathbb and the set of integers \mathbb, in which each prime p is related to each integer z that is a Divisibility, multiple of p, but not to an integer that is not a Multiple (mathematics), multiple of p. In this relation, for instance, the prime number 2 is related to numbers such as -4, 0, 6, 10, but not to 1 or 9, just as the prime number 3 is related to 0, 6, and 9, but not to 4 or 13. Binary relations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Primitive Recursive Function
In computability theory, a primitive recursive function is, roughly speaking, a function that can be computed by a computer program whose loops are all "for" loops (that is, an upper bound of the number of iterations of every loop is fixed before entering the loop). Primitive recursive functions form a strict subset of those general recursive functions that are also total functions. The importance of primitive recursive functions lies in the fact that most computable functions that are studied in number theory (and more generally in mathematics) are primitive recursive. For example, addition and division, the factorial and exponential function, and the function which returns the ''n''th prime are all primitive recursive. In fact, for showing that a computable function is primitive recursive, it suffices to show that its time complexity is bounded above by a primitive recursive function of the input size. It is hence not particularly easy to devise a computable function th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Modulo Function
In computing and mathematics, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another, the latter being called the '' modulus'' of the operation. Given two positive numbers and , modulo (often abbreviated as ) is the remainder of the Euclidean division of by , where is the dividend and is the divisor. For example, the expression "5 mod 2" evaluates to 1, because 5 divided by 2 has a quotient of 2 and a remainder of 1, while "9 mod 3" would evaluate to 0, because 9 divided by 3 has a quotient of 3 and a remainder of 0. Although typically performed with and both being integers, many computing systems now allow other types of numeric operands. The range of values for an integer modulo operation of is 0 to . mod 1 is always 0. When exactly one of or is negative, the basic definition breaks down, and programming languages differ in how these values are defined. Variants of the definition In mathematics, the re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Floor Function
In mathematics, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or . For example, for floor: , , and for ceiling: , and . The floor of is also called the integral part, integer part, greatest integer, or entier of , and was historically denoted (among other notations). However, the same term, ''integer part'', is also used for truncation towards zero, which differs from the floor function for negative numbers. For an integer , . Although and produce graphs that appear exactly alike, they are not the same when the value of is an exact integer. For example, when , . However, if , then , while . Notation The ''integral part'' or ''integer part'' of a number ( in the original) was first defined in 1798 by Adrien-Marie Legendre in his proof of the Legendre's formula. Ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Power Of Two
A power of two is a number of the form where is an integer, that is, the result of exponentiation with number 2, two as the Base (exponentiation), base and integer as the exponent. In the fast-growing hierarchy, is exactly equal to f_1^n(1). In the Hardy hierarchy, is exactly equal to H_(1). Powers of two with Sign (mathematics)#Terminology for signs, non-negative exponents are integers: , , and is two multiplication, multiplied by itself times. The first ten powers of 2 for non-negative values of are: :1, 2, 4, 8, 16 (number), 16, 32 (number), 32, 64 (number), 64, 128 (number), 128, 256 (number), 256, 512 (number), 512, ... By comparison, powers of two with negative exponents are fractions: for positive integer , is one half multiplied by itself times. Thus the first few negative powers of 2 are , , , , etc. Sometimes these are called ''inverse powers of two'' because each is the multiplicative inverse of a positive power of two. Base of the binary numeral sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binary Representation
A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A ''binary number'' may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two. The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |