|
Autonomous Convergence Theorem
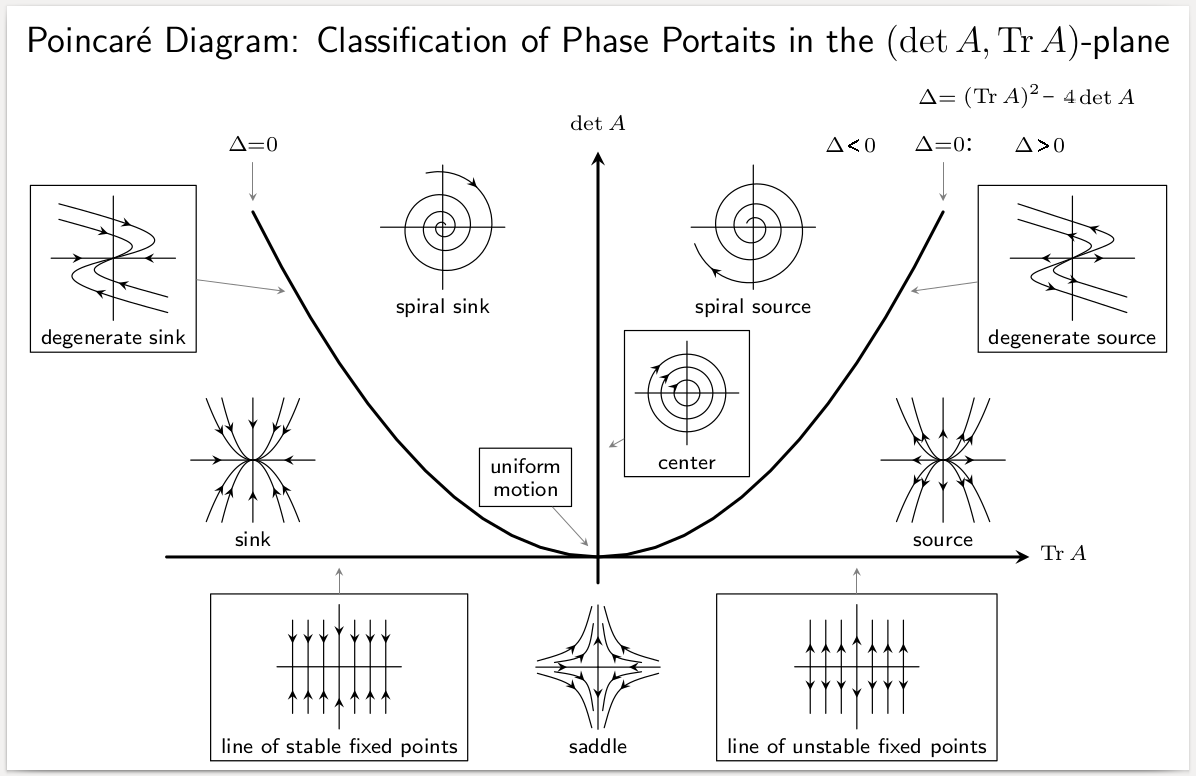
In mathematics, an autonomous convergence theorem is one of a family of related theorems which specify conditions guaranteeing global asymptotic stability of a continuous autonomous dynamical system. History The Markus–Yamabe conjecture was formulated as an attempt to give conditions for global stability of continuous dynamical systems in two dimensions. However, the Markus–Yamabe conjecture does not hold for dimensions higher than two, a problem which autonomous convergence theorems attempt to address. The first autonomous convergence theorem was constructed by Russell Smith. This theorem was later refined by Michael Li and James Muldowney. An example autonomous convergence theorem A comparatively simple autonomous convergence theorem is as follows: :Let x be a vector in some space X \subseteq \mathbb^n, evolving according to an autonomous differential equation \dot = f(x). Suppose that X is convex and forward invariant under f, and that there exists a fixed po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Matrix And Determinant
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian in literature. Suppose is a function such that each of its first-order partial derivatives exist on . This function takes a point as input and produces the vector as output. Then the Jacobian matrix of is defined to be an matrix, denoted by , whose th entry is \mathbf J_ = \frac, or explicitly :\mathbf J = \begin \dfrac & \cdots & \dfrac \end = \begin \nabla^ f_1 \\ \vdots \\ \nabla^ f_m \end = \begin \dfrac & \cdots & \dfrac\\ \vdots & \ddots & \vdots\\ \dfrac & \cdots ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff distance. In dynamical systems, an orbit is called ''Lyapunov stable'' if the forward orbit of any point is in a small enough neighborhood or it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable circumstances, the question may be reduced to a well-studied problem involvi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates (e.g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas. Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pugh's Closing Lemma
In mathematics, Pugh's closing lemma is a result that links periodic orbit solutions of differential equations to chaotic behaviour. It can be formally stated as follows: :Let f:M \to M be a C^1 diffeomorphism of a compact smooth manifold M . Given a nonwandering point x of f , there exists a diffeomorphism g arbitrarily close to f in the C^1 topology of \operatorname^1(M) such that x is a periodic point of g . Interpretation Pugh's closing lemma means, for example, that any chaotic set in a bounded continuous dynamical system corresponds to a periodic orbit in a different but closely related dynamical system. As such, an open set of conditions on a bounded continuous dynamical system that rules out periodic behaviour also implies that the system cannot behave chaotically; this is the basis of some autonomous convergence theorems. See also *Smale's problems Smale's problems are a list of eighteen unsolved problems in mathematics proposed by Steve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit (dynamics)
In mathematics, specifically in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. It can be understood as the subset of phase space covered by the trajectory of the dynamical system under a particular set of initial conditions, as the system evolves. As a phase space trajectory is uniquely determined for any given set of phase space coordinates, it is not possible for different orbits to intersect in phase space, therefore the set of all orbits of a dynamical system is a partition of the phase space. Understanding the properties of orbits by using topological methods is one of the objectives of the modern theory of dynamical systems. For discrete-time dynamical systems, the orbits are sequences; for real dynamical systems, the orbits are curves; and for holomorphic dynamical systems, the orbits are Riemann surfaces. Definition Given a dynamical system (''T'', ''M'', Φ) with ''T'' a group, ''M'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Set
In mathematical analysis and related areas of mathematics, a set is called ''bounded'' if all of its points are within a certain distance of each other. Conversely, a set which is not bounded is called ''unbounded''. The word "bounded" makes no sense in a general topological space without a corresponding metric. '' Boundary'' is a distinct concept: for example, a circle in isolation is a boundaryless bounded set, while the half plane is unbounded yet has a boundary. A bounded set is not necessarily a closed set and vice versa. For example, a subset ''S'' of a 2-dimensional real space R''2'' constrained by two parabolic curves ''x''2 + 1 and ''x''2 - 1 defined in a Cartesian coordinate system is closed by the curves but not bounded (so unbounded). Definition in the real numbers A set ''S'' of real numbers is called ''bounded from above'' if there exists some real number ''k'' (not necessarily in ''S'') such that ''k'' ≥ '' s'' for all ''s'' in ''S''. The number ''k'' is calle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
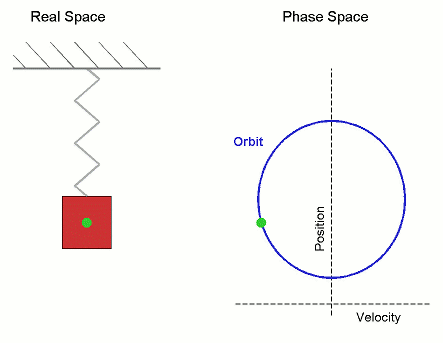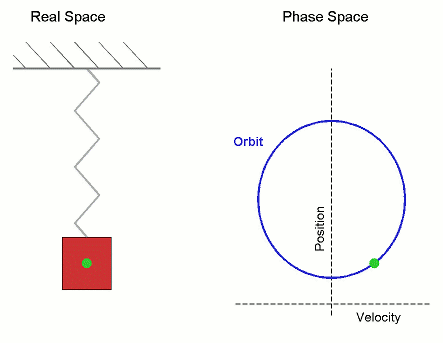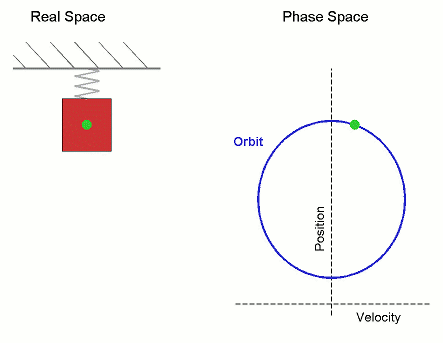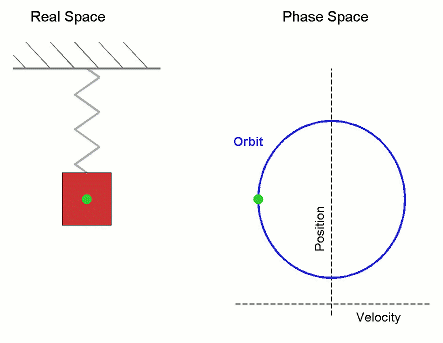
Phase Space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. It is the outer product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Introduction In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-space trajectory for the system) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete trajectory is defined by position and momentum, simultaneously. The mass might be a projectile or a satellite. For example, it can be an orbit — the path of a planet, asteroid, or comet as it travels around a central mass. In control theory, a trajectory is a time-ordered set of states of a dynamical system (see e.g. Poincaré map). In discrete mathematics, a trajectory is a sequence (f^k(x))_ of values calculated by the iterated application of a mapping f to an element x of its source. Physics of trajectories A familiar example of a trajectory is the path of a projectile, such as a thrown ball or rock. In a significantly simplified model, the object moves only under the influence of a uniform gravitational force field. This can be a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norm (mathematics)
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in an Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude of the vector. This norm can be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm, but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meanings. It may be a synonym of "seminorm". A pseudonorm may satisfy the same axioms as a norm, wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Fixed-point Theorem
In mathematics, the Banach fixed-point theorem (also known as the contraction mapping theorem or contractive mapping theorem) is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points. It can be understood as an abstract formulation of Picard's method of successive approximations. The theorem is named after Stefan Banach (1892–1945) who first stated it in 1922. Statement ''Definition.'' Let (X, d) be a complete metric space. Then a map T : X \to X is called a contraction mapping on ''X'' if there exists q \in non-empty complete metric space with a contraction mapping T : X \to X. Then ''T'' admits a unique Fixed point (mathematics)">fixed-point x^* in ''X'' (i.e. T(x^*) = x^*). Furthermore, x^* can be found as follows: start with an arbitrary element x_0 \in X and define a sequence (x_n)_ by x_n = T(x_) for n \geq 1. Then \li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |