Polarization (waves)

, or , is a property of transverse waves which specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. One example of a polarized transverse wave is vibrations traveling along a taut string, for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic waves such as light and radio waves, gravitational waves, and transverse sound waves ( shear waves) in solids.

An electromagnetic wave such as light consists of a coupled oscillating electric field and magnetic field which are always perpendicular to each other. Different states of polarization correspond to different relationships between polarization and the direction of propagation. In linear polarization, the fields oscillate in a single direction. In circular or elliptical polarization, the fields rotate at a constant rate in a plane as the wave travels, either in the right-hand or in the left-hand direction.

Light or other electromagnetic radiation from many sources, such as the sun, flames, and incandescent lamps, consists of short wave trains with an equal mixture of polarizations; this is called '' unpolarized light''. Polarized light can be produced by passing unpolarized light through a polarizer, which allows waves of only one polarization to pass through. The most common optical materials do not affect the polarization of light, but some materials—those that exhibit birefringence, dichroism, or optical activity—affect light differently depending on its polarization. Some of these are used to make polarizing filters. Light also becomes partially polarized when it reflects at an angle from a surface.

According to quantum mechanics, electromagnetic waves can also be viewed as streams of particles called photons. When viewed in this way, the polarization of an electromagnetic wave is determined by a quantum mechanical property of photons called their spin. A photon has one of two possible spins: it can either spin in a right hand sense or a left hand sense about its direction of travel. Circularly polarized electromagnetic waves are composed of photons with only one type of spin, either right- or left-hand. Linearly polarized waves consist of photons that are in a superposition of right and left circularly polarized states, with equal amplitude and phases synchronized to give oscillation in a plane.

Polarization is an important parameter in areas of science dealing with transverse waves, such as optics, seismology, radio, and microwaves. Especially impacted are technologies such as lasers, wireless and optical fiber telecommunications, and radar.

Introduction

Wave propagation and polarization

Most sources of light are classified as incoherent and unpolarized (or only "partially polarized") because they consist of a random mixture of waves having different spatial characteristics, frequencies (wavelengths), phases, and polarization states. However, for understanding electromagnetic waves and polarization in particular, it is easier to just consider coherent plane waves; these are sinusoidal waves of one particular direction (or wavevector), frequency, phase, and polarization state. Characterizing an optical system in relation to a plane wave with those given parameters can then be used to predict its response to a more general case, since a wave with any specified spatial structure can be decomposed into a combination of plane waves (its so-called angular spectrum). Incoherent states can be modeled stochastically as a weighted combination of such uncorrelated waves with some distribution of frequencies (its ''spectrum''), phases, and polarizations.

Transverse electromagnetic waves

Electromagnetic waves (such as light), traveling in free space or another homogeneous isotropic non-attenuating medium, are properly described as transverse waves, meaning that a plane wave's electric field vector and magnetic field are each in some direction perpendicular to (or "transverse" to) the direction of wave propagation; and are also perpendicular to each other. By convention, the "polarization" direction of an electromagnetic wave is given by its electric field vector. Considering a monochromatic plane wave of optical frequency (light of vacuum wavelength has a frequency of where is the speed of light), let us take the direction of propagation as the axis. Being a transverse wave the and fields must then contain components only in the and directions whereas . Using complex (or phasor) notation, the instantaneous physical electric and magnetic fields are given by the real parts of the complex quantities occurring in the following equations. As a function of time and spatial position (since for a plane wave in the direction the fields have no dependence on or ) these complex fields can be written as:
$\vec(z, t) = \begin e_x \\ e_y \\ 0 \end\; e^ = \begin e_x \\ e_y \\ 0 \end\; e^$
and
$\vec(z, t) = \begin h_x \\ h_y \\ 0 \end\; e^ = \begin h_x \\ h_y \\ 0 \end\; e^,$
where is the wavelength (whose refractive index is ) and is the period of the wave. Here , , , and are complex numbers. In the second more compact form, as these equations are customarily expressed, these factors are described using the wavenumber and angular frequency (or "radian frequency") . In a more general formulation with propagation restricted to the direction, then the spatial dependence is replaced by where is called the wave vector, the magnitude of which is the wavenumber.

Thus the leading vectors and each contain up to two nonzero (complex) components describing the amplitude and phase of the wave's and polarization components (again, there can be no polarization component for a transverse wave in the direction). For a given medium with a characteristic impedance , is related to by:
$\begin h_y &= \frac \\ h_x &= -\frac. \end$

In a dielectric, is real and has the value , where is the refractive index and is the impedance of free space. The impedance will be complex in a conducting medium. Note that given that relationship, the dot product of and must be zero:
$\begin \vec\left(\vec, t\right) \cdot \vec\left(\vec, t\right) &= e_x h_x + e_y h_y + e_z h_z \\ &= e_x \left(-\frac\right) + e_y \left(\frac\right) + 0 \cdot 0 \\ &= 0, \end$
indicating that these vectors are orthogonal (at right angles to each other), as expected.

Knowing the propagation direction ( in this case) and , one can just as well specify the wave in terms of just and describing the electric field. The vector containing and (but without the component which is necessarily zero for a transverse wave) is known as a Jones vector. In addition to specifying the polarization state of the wave, a general Jones vector also specifies the overall magnitude and phase of that wave. Specifically, the intensity of the light wave is proportional to the sum of the squared magnitudes of the two electric field components:
$I = \left(\left, e_x\^2 + \left, e_y\^2\right) \, \frac$

However, the wave's ''state of polarization'' is only dependent on the (complex) ratio of to . So let us just consider waves whose ; this happens to correspond to an intensity of about in free space (where ). And because the absolute phase of a wave is unimportant in discussing its polarization state, let us stipulate that the phase of is zero; in other words is a real number while may be complex. Under these restrictions, and can be represented as follows:
$\begin e_x &= \sqrt \\ e_y &= \sqrt\, e^, \end$
where the polarization state is now fully parameterized by the value of (such that ) and the relative phase .

Non-transverse waves

In addition to transverse waves, there are many wave motions where the oscillation is not limited to directions perpendicular to the direction of propagation. These cases are far beyond the scope of the current article, which concentrates on transverse waves (such as most electromagnetic waves in bulk media), but one should be aware of cases where the polarization of a coherent wave cannot be described simply using a Jones vector, as we have just done.

Just considering electromagnetic waves, we note that the preceding discussion strictly applies to plane waves in a homogeneous isotropic non-attenuating medium, whereas in an anisotropic medium (such as birefringent crystals as discussed below) the electric or magnetic field may have longitudinal as well as transverse components. In those cases the electric displacement and magnetic flux density still obey the above geometry but due to anisotropy in the electric susceptibility (or in the magnetic permeability), now given by a tensor, the direction of (or ) may differ from that of (or ). Even in isotropic media, so-called inhomogeneous waves can be launched into a medium whose refractive index has a significant imaginary part (or " extinction coefficient") such as metals; these fields are also not strictly transverse. Surface waves or waves propagating in a waveguide (such as an optical fiber) are generally transverse waves, but might be described as an electric or magnetic transverse mode, or a hybrid mode.

Even in free space, longitudinal field components can be generated in focal regions, where the plane wave approximation breaks down. An extreme example is radially or tangentially polarized light, at the focus of which the electric or magnetic field respectively is longitudinal (along the direction of propagation).

For longitudinal waves such as sound waves in fluids, the direction of oscillation is by definition along the direction of travel, so the issue of polarization is normally not even mentioned. On the other hand, sound waves in a bulk solid can be transverse as well as longitudinal, for a total of three polarization components. In this case, the transverse polarization is associated with the direction of the shear stress and displacement in directions perpendicular to the propagation direction, while the longitudinal polarization describes compression of the solid and vibration along the direction of propagation. The differential propagation of transverse and longitudinal polarizations is important in seismology.

Polarization state

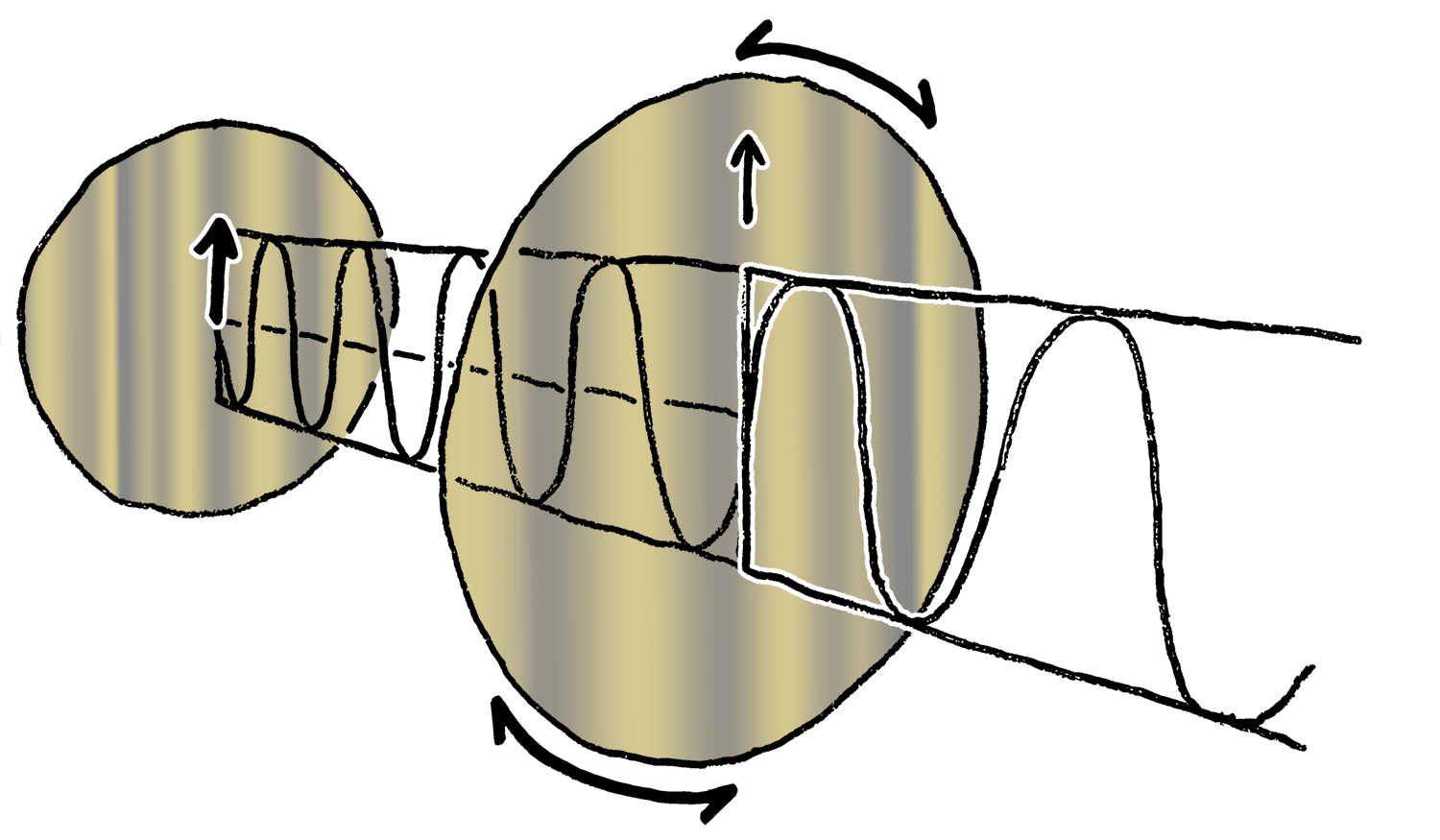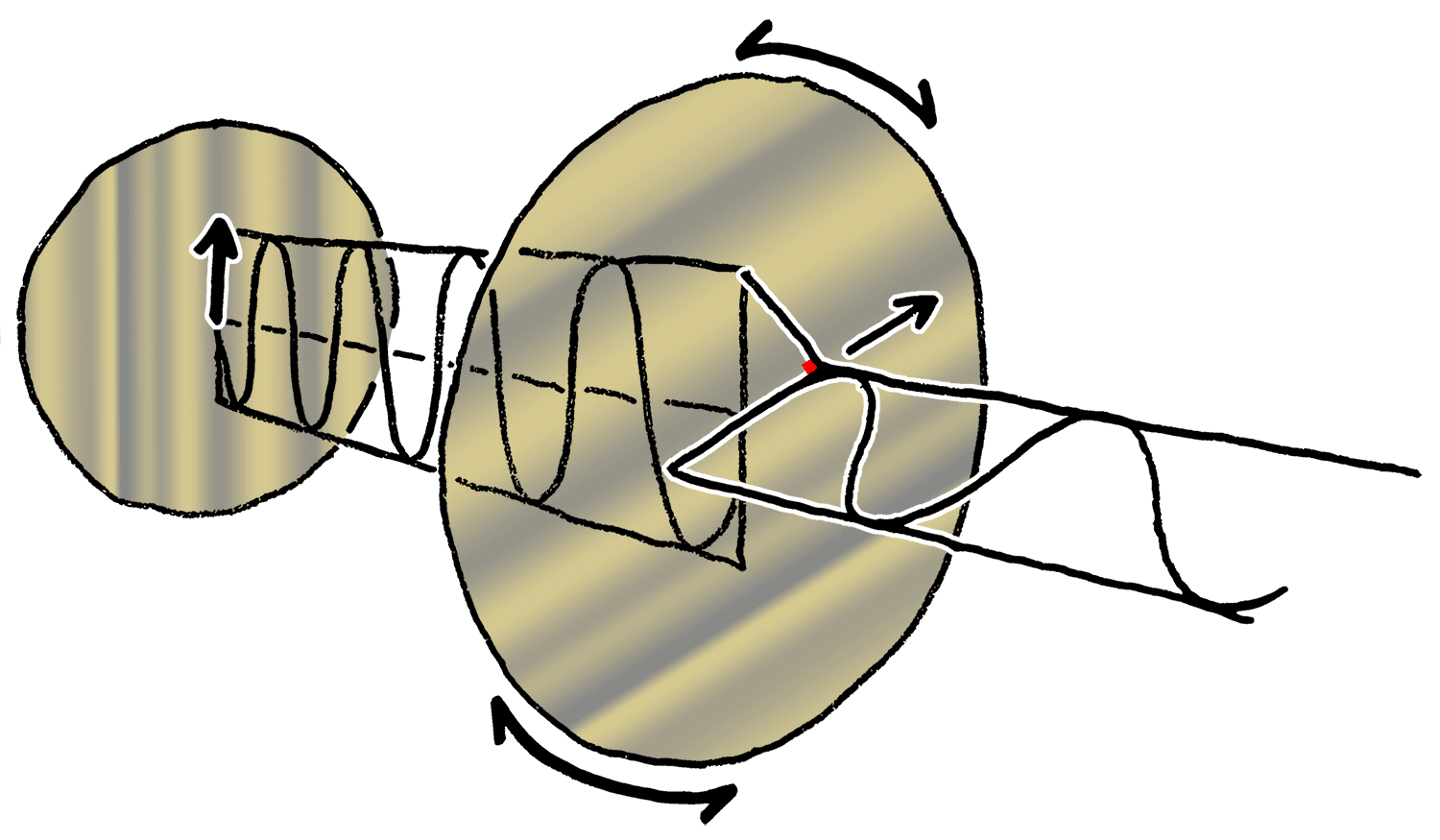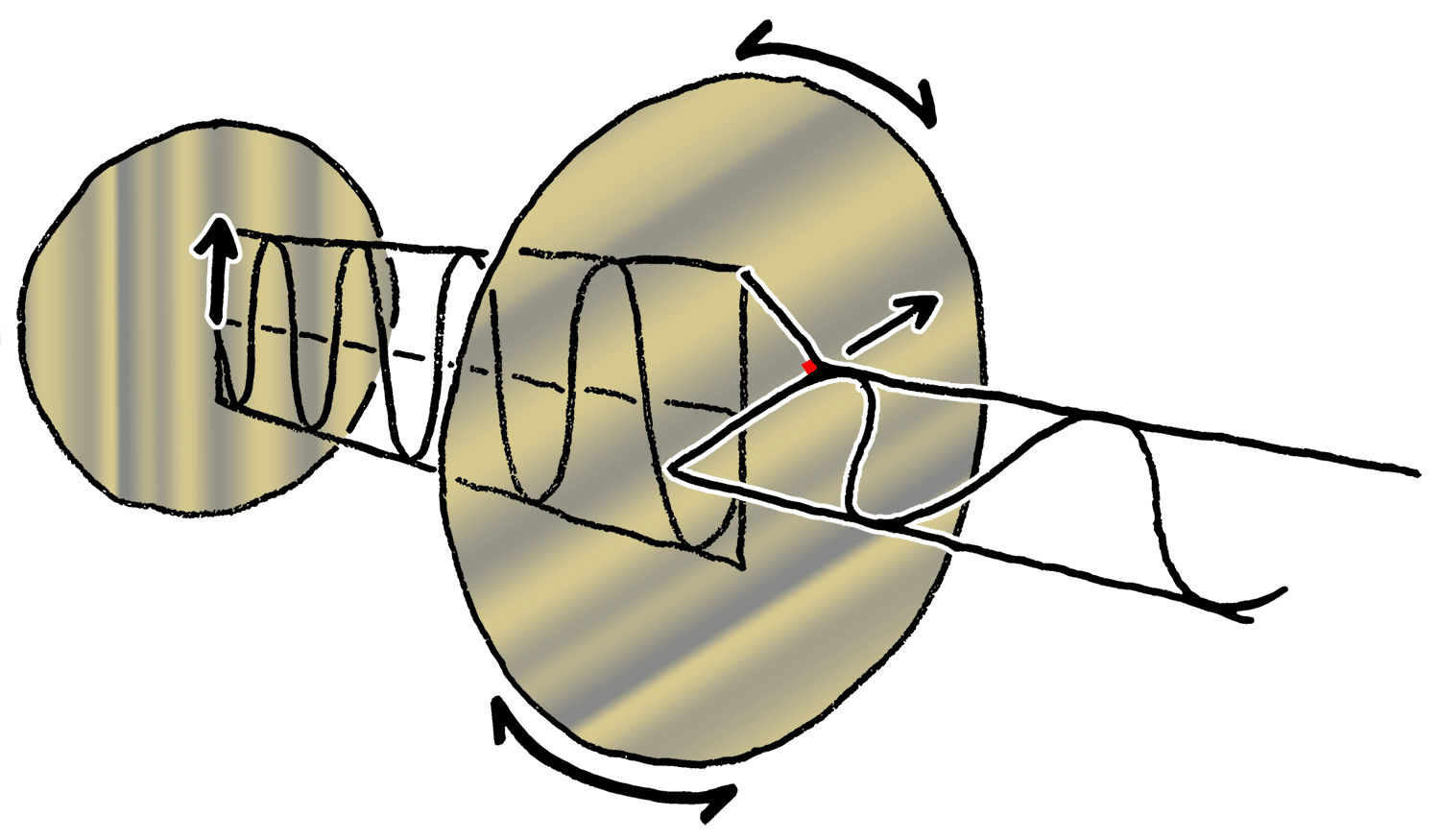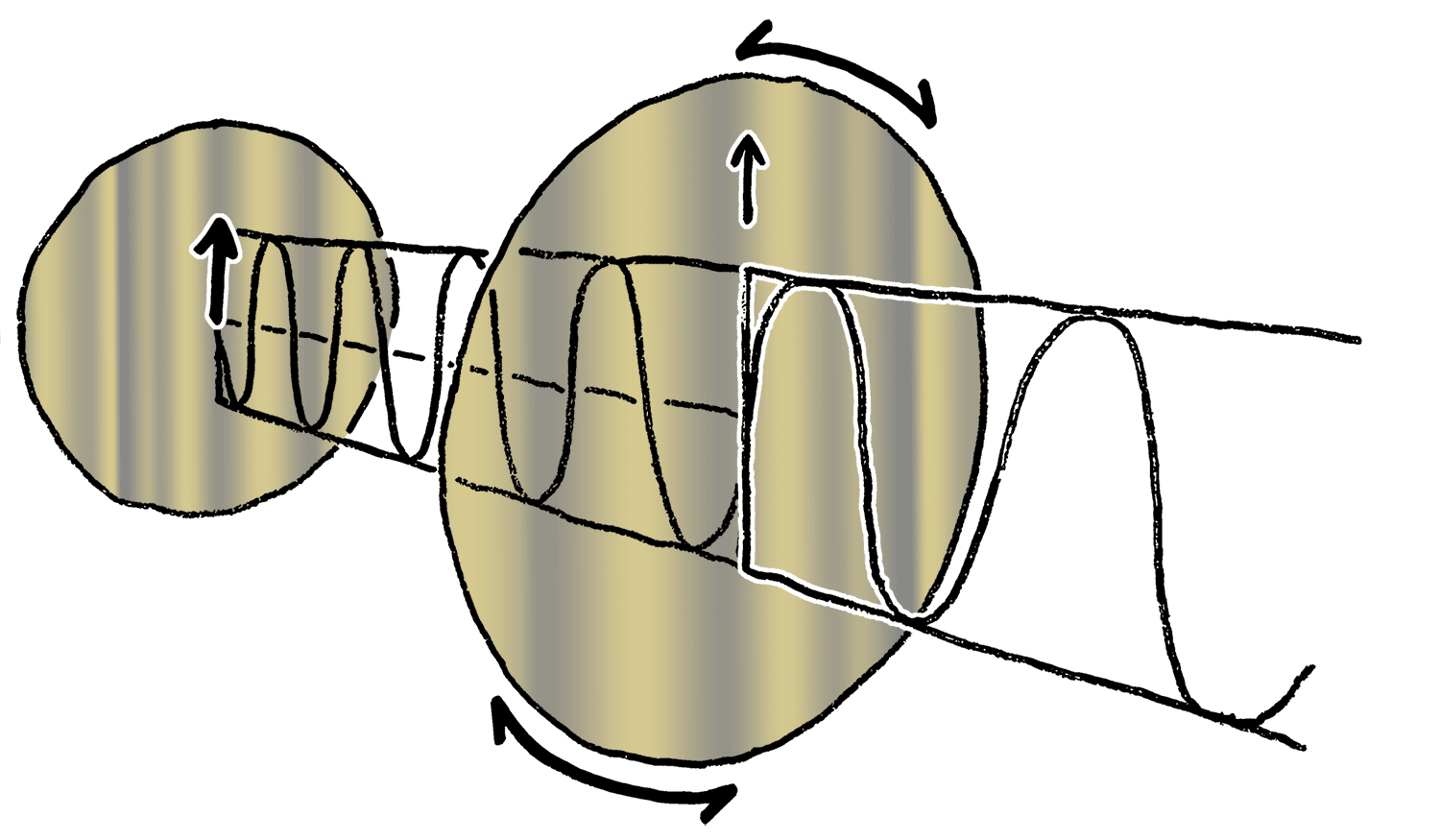
Polarization can be defined in terms of pure polarization states with only a coherent sinusoidal wave at one optical frequency. The vector in the adjacent diagram might describe the oscillation of the electric field emitted by a single-mode laser (whose oscillation frequency would be typically times faster). The field oscillates in the -plane, along the page, with the wave propagating in the direction, perpendicular to the page.
The first two diagrams below trace the electric field vector over a complete cycle for linear polarization at two different orientations; these are each considered a distinct ''state of polarization'' (SOP). The linear polarization at 45° can also be viewed as the addition of a horizontally linearly polarized wave (as in the leftmost figure) and a vertically polarized wave of the same amplitude .

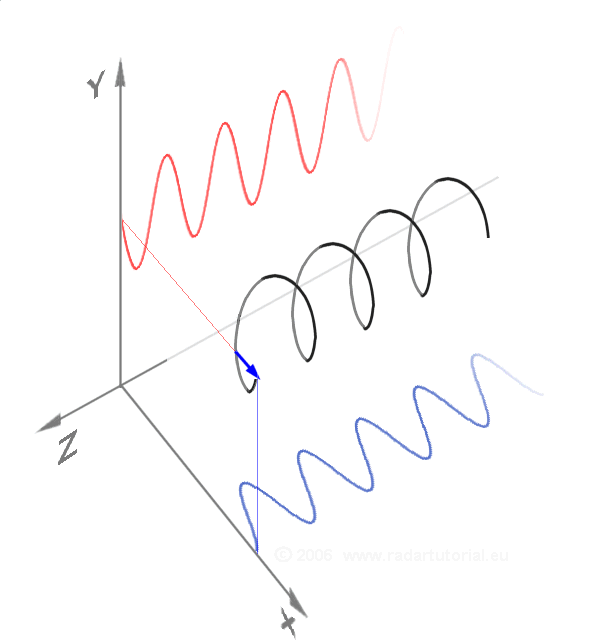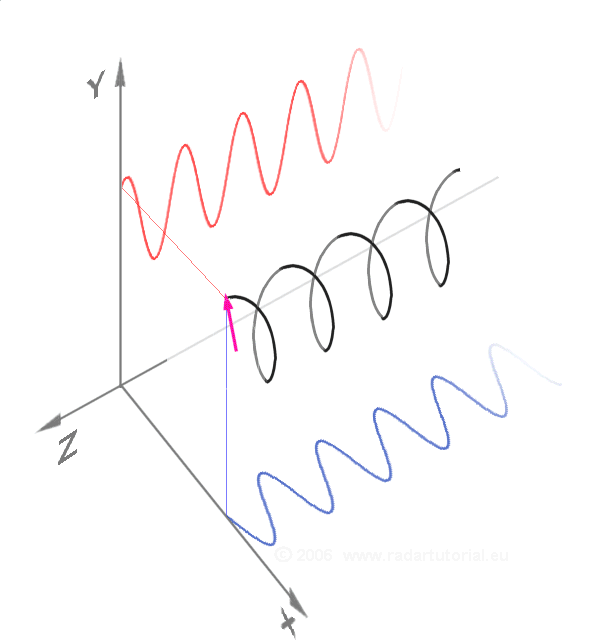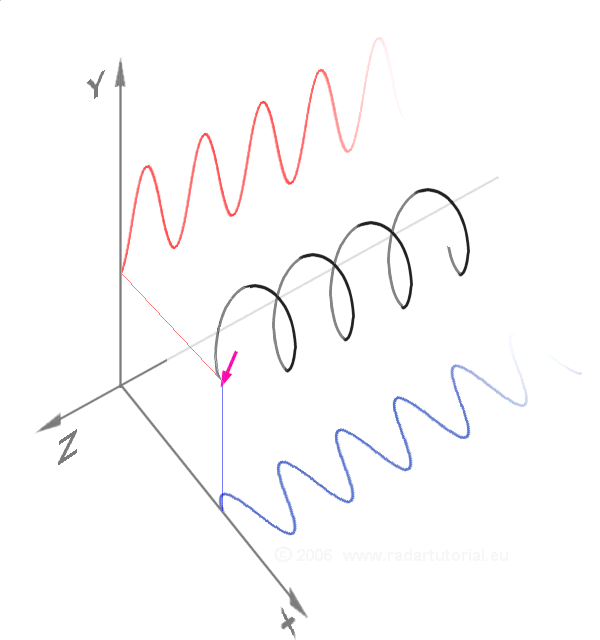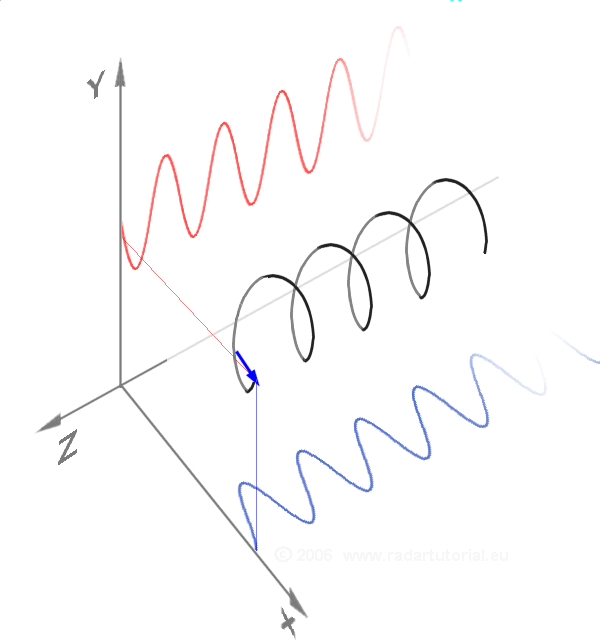
Now if one were to introduce a phase shift in between those horizontal and vertical polarization components, one would generally obtain elliptical polarization as is shown in the third figure. When the phase shift is exactly ±90°, and the amplitudes are the same, then circular polarization is produced (fourth and fifth figures). Circular polarization can be created by sending linearly polarized light through a quarter-wave plate oriented at 45° to the linear polarization to create two components of the same amplitude with the required phase shift. The superposition of the original and phase-shifted components causes a rotating electric field vector, which is depicted in the animation on the right. Note that circular or elliptical polarization can involve either a clockwise or counterclockwise rotation of the field, depending on the relative phases of the components. These correspond to distinct polarization states, such as the two circular polarizations shown above.

The orientation of the and axes used in this description is arbitrary. The choice of such a coordinate system and viewing the polarization ellipse in terms of the and polarization components, corresponds to the definition of the Jones vector (below) in terms of those basis polarizations. Axes are selected to suit a particular problem, such as being in the plane of incidence. Since there are separate reflection coefficients for the linear polarizations in and orthogonal to the plane of incidence (''p'' and ''s'' polarizations, see below), that choice greatly simplifies the calculation of a wave's reflection from a surface.

Any pair of orthogonal polarization states may be used as basis functions, not just linear polarizations. For instance, choosing right and left circular polarizations as basis functions simplifies the solution of problems involving circular birefringence (optical activity) or circular dichroism.

Polarization ellipse

For a purely polarized monochromatic wave the electric field vector over one cycle of oscillation traces out an ellipse.
A polarization state can then be described in relation to the geometrical parameters of the ellipse, and its "handedness", that is, whether the rotation around the ellipse is clockwise or counter clockwise. One parameterization of the elliptical figure specifies the orientation angle , defined as the angle between the major axis of the ellipse and the -axis along with the ellipticity , the ratio of the ellipse's major to minor axis. (also known as the axial ratio). The ellipticity parameter is an alternative parameterization of an ellipse's eccentricity $e=\sqrt,$ or the ellipticity angle, $\chi=\arctan b/a$ $=\arctan 1/\varepsilon$ as is shown in the figure. The angle is also significant in that the latitude (angle from the equator) of the polarization state as represented on the Poincaré sphere (see below) is equal to . The special cases of linear and circular polarization correspond to an ellipticity of infinity and unity (or of zero and 45°) respectively.

Jones vector

Full information on a completely polarized state is also provided by the amplitude and phase of oscillations in two components of the electric field vector in the plane of polarization. This representation was used above to show how different states of polarization are possible. The amplitude and phase information can be conveniently represented as a two-dimensional complex vector (the Jones vector):

$\mathbf = \begin a_1 e^ \\ a_2 e^ \end.$

Here and denote the amplitude of the wave in the two components of the electric field vector, while and represent the phases. The product of a Jones vector with a complex number of unit modulus gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase. The basis vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.

Coordinate frame

Regardless of whether polarization state is represented using geometric parameters or Jones vectors, implicit in the parameterization is the orientation of the coordinate frame. This permits a degree of freedom, namely rotation about the propagation direction. When considering light that is propagating parallel to the surface of the Earth, the terms "horizontal" and "vertical" polarization are often used, with the former being associated with the first component of the Jones vector, or zero azimuth angle. On the other hand, in astronomy the equatorial coordinate system is generally used instead, with the zero azimuth (or position angle, as it is more commonly called in astronomy to avoid confusion with the horizontal coordinate system) corresponding to due north.

''s'' and ''p'' designations

Another coordinate system frequently used relates to the '' plane of incidence''. This is the plane made by the incoming propagation direction and the vector perpendicular to the plane of an interface, in other words, the plane in which the ray travels before and after reflection or refraction. The component of the electric field parallel to this plane is termed ''p-like'' (parallel) and the component perpendicular to this plane is termed ''s-like'' (from , German for 'perpendicular'). Polarized light with its electric field along the plane of incidence is thus denoted ', while light whose electric field is normal to the plane of incidence is called '. ''P''-polarization is commonly referred to as ''transverse-magnetic'' (TM), and has also been termed ''pi-polarized'' or ''-polarized'', or ''tangential plane polarized''. ''S''-polarization is also called ''transverse-electric'' (TE), as well as ''sigma-polarized'' or ''σ-polarized'', or ''sagittal plane polarized''.

Degree of polarization

Degree of polarization (DOP) is a quantity used to describe the portion of an electromagnetic wave which is polarized. can be calculated from the Stokes parameters. A perfectly polarized wave has a of 100%, whereas an unpolarized wave has a of 0%. A wave which is partially polarized, and therefore can be represented by a superposition of a polarized and unpolarized component, will have a somewhere in between 0 and 100%. is calculated as the fraction of the total power that is carried by the polarized component of the wave.

can be used to map the strain field in materials when considering the of the photoluminescence. The polarization of the photoluminescence is related to the strain in a material by way of the given material's photoelasticity tensor.

is also visualized using the Poincaré sphere representation of a polarized beam. In this representation, is equal to the length of the vector measured from the center of the sphere.

Unpolarized and partially polarized light

Implications for reflection and propagation

Polarization in wave propagation

In a vacuum, the components of the electric field propagate at the speed of light, so that the phase of the wave varies in space and time while the polarization state does not. That is, the electric field vector of a plane wave in the direction follows:
$\mathbf(z + \Delta z, t + \Delta t) = \mathbf(z, t) e^,$

where is the wavenumber. As noted above, the instantaneous electric field is the real part of the product of the Jones vector times the phase factor When an electromagnetic wave interacts with matter, its propagation is altered according to the material's (complex) index of refraction. When the real or imaginary part of that refractive index is dependent on the polarization state of a wave, properties known as birefringence and polarization dichroism (or diattenuation) respectively, then the polarization state of a wave will generally be altered.

In such media, an electromagnetic wave with any given state of polarization may be decomposed into two orthogonally polarized components that encounter different propagation constants. The effect of propagation over a given path on those two components is most easily characterized in the form of a complex transformation matrix known as a Jones matrix:
$\mathbf = \mathbf\mathbf.$

The Jones matrix due to passage through a transparent material is dependent on the propagation distance as well as the birefringence. The birefringence (as well as the average refractive index) will generally be dispersive, that is, it will vary as a function of optical frequency (wavelength). In the case of non-birefringent materials, however, the Jones matrix is the identity matrix (multiplied by a scalar phase factor and attenuation factor), implying no change in polarization during propagation.

For propagation effects in two orthogonal modes, the Jones matrix can be written as
$\mathbf = \mathbf\begin g_1 & 0 \\ 0 & g_2 \end\mathbf^,$

where and are complex numbers describing the phase delay and possibly the amplitude attenuation due to propagation in each of the two polarization eigenmodes. is a unitary matrix representing a change of basis from these propagation modes to the linear system used for the Jones vectors; in the case of linear birefringence or diattenuation the modes are themselves linear polarization states so and can be omitted if the coordinate axes have been chosen appropriately.

Birefringence

In a birefringent substance, electromagnetic waves of different polarizations travel at different speeds ( phase velocities). As a result, when unpolarized waves travel through a plate of birefringent material, one polarization component has a shorter wavelength than the other, resulting in a phase difference between the components which increases the further the waves travel through the material. The Jones matrix is a unitary matrix: . Media termed diattenuating (or '' dichroic'' in the sense of polarization), in which only the amplitudes of the two polarizations are affected differentially, may be described using a Hermitian matrix (generally multiplied by a common phase factor). In fact, since matrix may be written as the product of unitary and positive Hermitian matrices, light propagation through any sequence of polarization-dependent optical components can be written as the product of these two basic types of transformations.

In birefringent media there is no attenuation, but two modes accrue a differential phase delay. Well known manifestations of linear birefringence (that is, in which the basis polarizations are orthogonal linear polarizations) appear in optical wave plates/retarders and many crystals. If linearly polarized light passes through a birefringent material, its state of polarization will generally change, its polarization direction is identical to one of those basis polarizations. Since the phase shift, and thus the change in polarization state, is usually wavelength-dependent, such objects viewed under white light in between two polarizers may give rise to colorful effects, as seen in the accompanying photograph.

Circular birefringence is also termed optical activity, especially in chiral fluids, or Faraday rotation, when due to the presence of a magnetic field along the direction of propagation. When linearly polarized light is passed through such an object, it will exit still linearly polarized, but with the axis of polarization rotated. A combination of linear and circular birefringence will have as basis polarizations two orthogonal elliptical polarizations; however, the term "elliptical birefringence" is rarely used.

One can visualize the case of linear birefringence (with two orthogonal linear propagation modes) with an incoming wave linearly polarized at a 45° angle to those modes. As a differential phase starts to accrue, the polarization becomes elliptical, eventually changing to purely circular polarization (90° phase difference), then to elliptical and eventually linear polarization (180° phase) perpendicular to the original polarization, then through circular again (270° phase), then elliptical with the original azimuth angle, and finally back to the original linearly polarized state (360° phase) where the cycle begins anew. In general the situation is more complicated and can be characterized as a rotation in the Poincaré sphere about the axis defined by the propagation modes. Examples for linear (blue), circular (red), and elliptical (yellow) birefringence are shown in the figure on the left. The total intensity and degree of polarization are unaffected. If the path length in the birefringent medium is sufficient, the two polarization components of a collimated beam (or ray) can exit the material with a positional offset, even though their final propagation directions will be the same (assuming the entrance face and exit face are parallel). This is commonly viewed using calcite crystals, which present the viewer with two slightly offset images, in opposite polarizations, of an object behind the crystal. It was this effect that provided the first discovery of polarization, by Erasmus Bartholinus in 1669.

Dichroism

Media in which transmission of one polarization mode is preferentially reduced are called '' dichroic'' or ''diattenuating''. Like birefringence, diattenuation can be with respect to linear polarization modes (in a crystal) or circular polarization modes (usually in a liquid).

Devices that block nearly all of the radiation in one mode are known as ' or simply "polarizers". This corresponds to in the above representation of the Jones matrix. The output of an ideal polarizer is a specific polarization state (usually linear polarization) with an amplitude equal to the input wave's original amplitude in that polarization mode. Power in the other polarization mode is eliminated. Thus if unpolarized light is passed through an ideal polarizer (where and ) exactly half of its initial power is retained. Practical polarizers, especially inexpensive sheet polarizers, have additional loss so that . However, in many instances the more relevant figure of merit is the polarizer's degree of polarization or extinction ratio, which involve a comparison of to . Since Jones vectors refer to waves' amplitudes (rather than intensity), when illuminated by unpolarized light the remaining power in the unwanted polarization will be of the power in the intended polarization.

Specular reflection

In addition to birefringence and dichroism in extended media, polarization effects describable using Jones matrices can also occur at (reflective) interface between two materials of different refractive index. These effects are treated by the Fresnel equations. Part of the wave is transmitted and part is reflected; for a given material those proportions (and also the phase of reflection) are dependent on the angle of incidence and are different for the ''s''- and ''p''-polarizations. Therefore, the polarization state of reflected light (even if initially unpolarized) is generally changed.

Any light striking a surface at a special angle of incidence known as Brewster's angle, where the reflection coefficient for ''p''-polarization is zero, will be reflected with only the ''s''-polarization remaining. This principle is employed in the so-called "pile of plates polarizer" (see figure) in which part of the ''s''-polarization is removed by reflection at each Brewster angle surface, leaving only the ''p''-polarization after transmission through many such surfaces. The generally smaller reflection coefficient of the ''p''-polarization is also the basis of polarized sunglasses; by blocking the ''s''- (horizontal) polarization, most of the glare due to reflection from a wet street, for instance, is removed.

In the important special case of reflection at normal incidence (not involving anisotropic materials) there is no particular ''s''- or ''p''-polarization. Both the and polarization components are reflected identically, and therefore the polarization of the reflected wave is identical to that of the incident wave. However, in the case of circular (or elliptical) polarization, the handedness of the polarization state is thereby reversed, since by convention this is specified relative to the direction of propagation. The circular rotation of the electric field around the axes called "right-handed" for a wave in the direction is "left-handed" for a wave in the direction. But in the general case of reflection at a nonzero angle of incidence, no such generalization can be made. For instance, right-circularly polarized light reflected from a dielectric surface at a grazing angle, will still be right-handed (but elliptically) polarized. Linear polarized light reflected from a metal at non-normal incidence will generally become elliptically polarized. These cases are handled using Jones vectors acted upon by the different Fresnel coefficients for the ''s''- and ''p''-polarization components.

Measurement techniques involving polarization

Some optical measurement techniques are based on polarization. In many other optical techniques polarization is crucial or at least must be taken into account and controlled; such examples are too numerous to mention.

Measurement of stress

In engineering, the phenomenon of stress induced birefringence allows for stresses in transparent materials to be readily observed. As noted above and seen in the accompanying photograph, the chromaticity of birefringence typically creates colored patterns when viewed in between two polarizers. As external forces are applied, internal stress induced in the material is thereby observed. Additionally, birefringence is frequently observed due to stresses "frozen in" at the time of manufacture. This is famously observed in cellophane tape whose birefringence is due to the stretching of the material during the manufacturing process.

Ellipsometry

Ellipsometry is a powerful technique for the measurement of the optical properties of a uniform surface. It involves measuring the polarization state of light following specular reflection from such a surface. This is typically done as a function of incidence angle or wavelength (or both). Since ellipsometry relies on reflection, it is not required for the sample to be transparent to light or for its back side to be accessible.

Ellipsometry can be used to model the (complex) refractive index of a surface of a bulk material. It is also very useful in determining parameters of one or more thin film layers deposited on a substrate. Due to their reflection properties, not only are the predicted magnitude of the ''p'' and ''s'' polarization components, but their relative phase shifts upon reflection, compared to measurements using an ellipsometer. A normal ellipsometer does not measure the actual reflection coefficient (which requires careful photometric calibration of the illuminating beam) but the ratio of the ''p'' and ''s'' reflections, as well as change of polarization ellipticity (hence the name) induced upon reflection by the surface being studied. In addition to use in science and research, ellipsometers are used in situ to control production processes for instance.

Geology

The property of (linear) birefringence is widespread in crystalline minerals, and indeed was pivotal in the initial discovery of polarization. In mineralogy, this property is frequently exploited using polarization microscopes, for the purpose of identifying minerals. See optical mineralogy for more details.

Sound waves in solid materials exhibit polarization. Differential propagation of the three polarizations through the earth is a crucial in the field of seismology. Horizontally and vertically polarized seismic waves ( shear waves) are termed SH and SV, while waves with longitudinal polarization ( compressional waves) are termed P-waves.

Autopsy

Similarly, polarization microscopes can be used to aid in the detection of foreign matter in biological tissue slices if it is birefringent; autopsies often mention (a lack of or presence of) "polarizable foreign debris."

Chemistry

We have seen (above) that the birefringence of a type of crystal is useful in identifying it, and thus detection of linear birefringence is especially useful in geology and mineralogy. Linearly polarized light generally has its polarization state altered upon transmission through such a crystal, making it stand out when viewed in between two crossed polarizers, as seen in the photograph, above. Likewise, in chemistry, rotation of polarization axes in a liquid solution can be a useful measurement. In a liquid, linear birefringence is impossible, but there may be circular birefringence when a chiral molecule is in solution. When the right and left handed enantiomers of such a molecule are present in equal numbers (a so-called racemic mixture) then their effects cancel out. However, when there is only one (or a preponderance of one), as is more often the case for organic molecules, a net circular birefringence (or '' optical activity'') is observed, revealing the magnitude of that imbalance (or the concentration of the molecule itself, when it can be assumed that only one enantiomer is present). This is measured using a polarimeter in which polarized light is passed through a tube of the liquid, at the end of which is another polarizer which is rotated in order to null the transmission of light through it.

Astronomy

In many areas of astronomy, the study of polarized electromagnetic radiation from outer space is of great importance. Although not usually a factor in the thermal radiation of stars, polarization is also present in radiation from coherent astronomical sources (e.g. hydroxyl or methanol masers), and incoherent sources such as the large radio lobes in active galaxies, and pulsar radio radiation (which may, it is speculated, sometimes be coherent), and is also imposed upon starlight by scattering from interstellar dust. Apart from providing information on sources of radiation and scattering, polarization also probes the interstellar magnetic field via Faraday rotation. The polarization of the cosmic microwave background is being used to study the physics of the very early universe. Synchrotron radiation is inherently polarized. It has been suggested that astronomical sources caused the chirality of biological molecules on Earth, but chirality selection on inorganic crystals has been proposed as an alternative theory.

Applications and examples

Polarized sunglasses

Unpolarized light, after being reflected by a specular (shiny) surface, generally obtains a degree of polarization. This phenomenon was observed in the early 1800s by the mathematician Étienne-Louis Malus, after whom Malus's law is named. Polarizing sunglasses exploit this effect to reduce glare from reflections by horizontal surfaces, notably the road ahead viewed at a grazing angle.

Wearers of polarized sunglasses will occasionally observe inadvertent polarization effects such as color-dependent birefringent effects, for example in toughened glass (e.g., car windows) or items made from transparent plastics, in conjunction with natural polarization by reflection or scattering. The polarized light from LCD monitors (see below) is extremely conspicuous when these are worn.

Sky polarization and photography

Polarization is observed in the light of the sky, as this is due to sunlight scattered by aerosols as it passes through Earth's atmosphere. The scattered light produces the brightness and color in clear skies. This partial polarization of scattered light can be used to darken the sky in photographs, increasing the contrast. This effect is most strongly observed at points on the sky making a 90° angle to the Sun. Polarizing filters use these effects to optimize the results of photographing scenes in which reflection or scattering by the sky is involved.

Sky polarization has been used for orientation in navigation. The Pfund sky compass was used in the 1950s when navigating near the poles of the Earth's magnetic field when neither the sun nor stars were visible (e.g., under daytime cloud or twilight). It has been suggested, controversially, that the Vikings exploited a similar device (the "sunstone") in their extensive expeditions across the North Atlantic in the 9th–11th centuries, before the arrival of the magnetic compass from Asia to Europe in the 12th century. Related to the sky compass is the " polar clock", invented by Charles Wheatstone in the late 19th century.

Display technologies

The principle of liquid-crystal display (LCD) technology relies on the rotation of the axis of linear polarization by the liquid crystal array. Light from the backlight (or the back reflective layer, in devices not including or requiring a backlight) first passes through a linear polarizing sheet. That polarized light passes through the actual liquid crystal layer which may be organized in pixels (for a TV or computer monitor) or in another format such as a seven-segment display or one with custom symbols for a particular product. The liquid crystal layer is produced with a consistent right (or left) handed chirality, essentially consisting of tiny helices. This causes circular birefringence, and is engineered so that there is a 90 degree rotation of the linear polarization state. However, when a voltage is applied across a cell, the molecules straighten out, lessening or totally losing the circular birefringence. On the viewing side of the display is another linear polarizing sheet, usually oriented at 90 degrees from the one behind the active layer. Therefore, when the circular birefringence is removed by the application of a sufficient voltage, the polarization of the transmitted light remains at right angles to the front polarizer, and the pixel appears dark. With no voltage, however, the 90 degree rotation of the polarization causes it to exactly match the axis of the front polarizer, allowing the light through. Intermediate voltages create intermediate rotation of the polarization axis and the pixel has an intermediate intensity. Displays based on this principle are widespread, and now are used in the vast majority of televisions, computer monitors and video projectors, rendering the previous CRT technology essentially obsolete. The use of polarization in the operation of LCD displays is immediately apparent to someone wearing polarized sunglasses, often making the display unreadable.

In a totally different sense, polarization encoding has become the leading (but not sole) method for delivering separate images to the left and right eye in stereoscopic displays used for 3D movies. This involves separate images intended for each eye either projected from two different projectors with orthogonally oriented polarizing filters or, more typically, from a single projector with time multiplexed polarization (a fast alternating polarization device for successive frames). Polarized 3D glasses with suitable polarizing filters ensure that each eye receives only the intended image. Historically such systems used linear polarization encoding because it was inexpensive and offered good separation. However, circular polarization makes separation of the two images insensitive to tilting of the head, and is widely used in 3-D movie exhibition today, such as the system from RealD. Projecting such images requires screens that maintain the polarization of the projected light when viewed in reflection (such as silver screens); a normal diffuse white projection screen causes depolarization of the projected images, making it unsuitable for this application.

Although now obsolete, CRT computer displays suffered from reflection by the glass envelope, causing glare from room lights and consequently poor contrast. Several anti-reflection solutions were employed to ameliorate this problem. One solution utilized the principle of reflection of circularly polarized light. A circular polarizing filter in front of the screen allows for the transmission of (say) only right circularly polarized room light. Now, right circularly polarized light (depending on the convention used) has its electric (and magnetic) field direction rotating clockwise while propagating in the +z direction. Upon reflection, the field still has the same direction of rotation, but now propagation is in the −z direction making the reflected wave ''left'' circularly polarized. With the right circular polarization filter placed in front of the reflecting glass, the unwanted light reflected from the glass will thus be in very polarization state that is ''blocked'' by that filter, eliminating the reflection problem. The reversal of circular polarization on reflection and elimination of reflections in this manner can be easily observed by looking in a mirror while wearing 3-D movie glasses which employ left- and right-handed circular polarization in the two lenses. Closing one eye, the other eye will see a reflection in which it cannot see itself; that lens appears black. However, the other lens (of the closed eye) will have the correct circular polarization allowing the closed eye to be easily seen by the open one.

Radio transmission and reception

All radio (and microwave) antennas used for transmitting or receiving are intrinsically polarized. They transmit in (or receive signals from) a particular polarization, being totally insensitive to the opposite polarization; in certain cases that polarization is a function of direction. Most antennas are nominally linearly polarized, but elliptical and circular polarization is a possibility. In the case of linear polarization, the same kind of filtering as described above, is possible. In the case of elliptical polarization (circular polarization is in reality just a kind of elliptical polarization where the length of both elasticity factors is the same), filtering out a single angle (e.g. 90°) will have virtually no impact as the wave at any time can be in any of the 360 degrees.

The vast majority of antennas are linearly polarized. In fact it can be shown from considerations of symmetry that an antenna that lies entirely in a plane which also includes the observer, can ''only'' have its polarization in the direction of that plane. This applies to many cases, allowing one to easily infer such an antenna's polarization at an intended direction of propagation. So a typical rooftop Yagi or log-periodic antenna with horizontal conductors, as viewed from a second station toward the horizon, is necessarily horizontally polarized. But a vertical " whip antenna" or AM broadcast tower used as an antenna element (again, for observers horizontally displaced from it) will transmit in the vertical polarization. A turnstile antenna with its four arms in the horizontal plane, likewise transmits horizontally polarized radiation toward the horizon. However, when that same turnstile antenna is used in the "axial mode" (upwards, for the same horizontally-oriented structure) its radiation is circularly polarized. At intermediate elevations it is elliptically polarized.

Polarization is important in radio communications because, for instance, if one attempts to use a horizontally polarized antenna to receive a vertically polarized transmission, the signal strength will be substantially reduced (or under very controlled conditions, reduced to nothing). This principle is used in satellite television in order to double the channel capacity over a fixed frequency band. The same frequency channel can be used for two signals broadcast in opposite polarizations. By adjusting the receiving antenna for one or the other polarization, either signal can be selected without interference from the other.

Especially due to the presence of the ground, there are some differences in propagation (and also in reflections responsible for TV ghosting) between horizontal and vertical polarizations. AM and FM broadcast radio usually use vertical polarization, while television uses horizontal polarization. At low frequencies especially, horizontal polarization is avoided. That is because the phase of a horizontally polarized wave is reversed upon reflection by the ground. A distant station in the horizontal direction will receive both the direct and reflected wave, which thus tend to cancel each other. This problem is avoided with vertical polarization. Polarization is also important in the transmission of radar pulses and reception of radar reflections by the same or a different antenna. For instance, back scattering of radar pulses by rain drops can be avoided by using circular polarization. Just as specular reflection of circularly polarized light reverses the handedness of the polarization, as discussed above, the same principle applies to scattering by objects much smaller than a wavelength such as rain drops. On the other hand, reflection of that wave by an irregular metal object (such as an airplane) will typically introduce a change in polarization and (partial) reception of the return wave by the same antenna.

The effect of free electrons in the ionosphere, in conjunction with the earth's magnetic field, causes Faraday rotation, a sort of circular birefringence. This is the same mechanism which can rotate the axis of linear polarization by electrons in interstellar space as mentioned below. The magnitude of Faraday rotation caused by such a plasma is greatly exaggerated at lower frequencies, so at the higher microwave frequencies used by satellites the effect is minimal. However, medium or short wave transmissions received following refraction by the ionosphere are strongly affected. Since a wave's path through the ionosphere and the earth's magnetic field vector along such a path are rather unpredictable, a wave transmitted with vertical (or horizontal) polarization will generally have a resulting polarization in an arbitrary orientation at the receiver.

Polarization and vision

Many animals are capable of perceiving some of the components of the polarization of light, e.g., linear horizontally polarized light. This is generally used for navigational purposes, since the linear polarization of sky light is always perpendicular to the direction of the sun. This ability is very common among the insects, including bees, which use this information to orient their communicative dances. Polarization sensitivity has also been observed in species of octopus, squid, cuttlefish, and mantis shrimp. In the latter case, one species measures all six orthogonal components of polarization, and is believed to have optimal polarization vision. The rapidly changing, vividly colored skin patterns of cuttlefish, used for communication, also incorporate polarization patterns, and mantis shrimp are known to have polarization selective reflective tissue. Sky polarization was thought to be perceived by pigeons, which was assumed to be one of their aids in homing, but research indicates this is a popular myth.

The naked human eye is weakly sensitive to polarization, without the need for intervening filters. Polarized light creates a very faint pattern near the center of the visual field, called Haidinger's brush. This pattern is very difficult to see, but with practice one can learn to detect polarized light with the naked eye.

Angular momentum using circular polarization

It is well known that electromagnetic radiation carries a certain linear momentum in the direction of propagation. In addition, however, light carries a certain angular momentum if it is circularly polarized (or partially so). In comparison with lower frequencies such as microwaves, the amount of angular momentum in light, even of pure circular polarization, compared to the same wave's linear momentum (or radiation pressure) is very small and difficult to even measure. However, it was utilized in an experiment to achieve speeds of up to 600 million revolutions per minute.

See also

Quantum Physics
* Plane of polarization
* Spin angular momentum of light
Optics
* Depolarizer (optics)
* Fluorescence anisotropy
* Glan–Taylor prism
* Kerr effect
* Nicol prism
* Pockels effect
* Polarization rotator
* Polarized light microscopy
* Polarizer
* Polaroid (polarizer)
* Radial polarization
* Rayleigh sky model
* Waveplate

References

Cited references

General references

*
*
*
*
*
*
*
*
*
*

External links

Feynman's lecture on polarization


Microscopic images made using polarization effects


* ttp://gerdbreitenbach.de/crystal/crystal.html A virtual polarization microscope
Polarization angle in satellite dishes


Molecular Expressions: Science, Optics and You — Polarization of Light
Interactive Java tutorial

Antenna Polarization

Animations of Linear, Circular and Elliptical Polarizations on YouTube

{{Authority control

Electromagnetic radiation
Antennas (radio)
Broadcast engineering
Physical optics