Logit Model on:
[Wikipedia]
[Google]
[Amazon]
 In statistics, the logistic model (or logit model) is a statistical model that models the
In statistics, the logistic model (or logit model) is a statistical model that models the
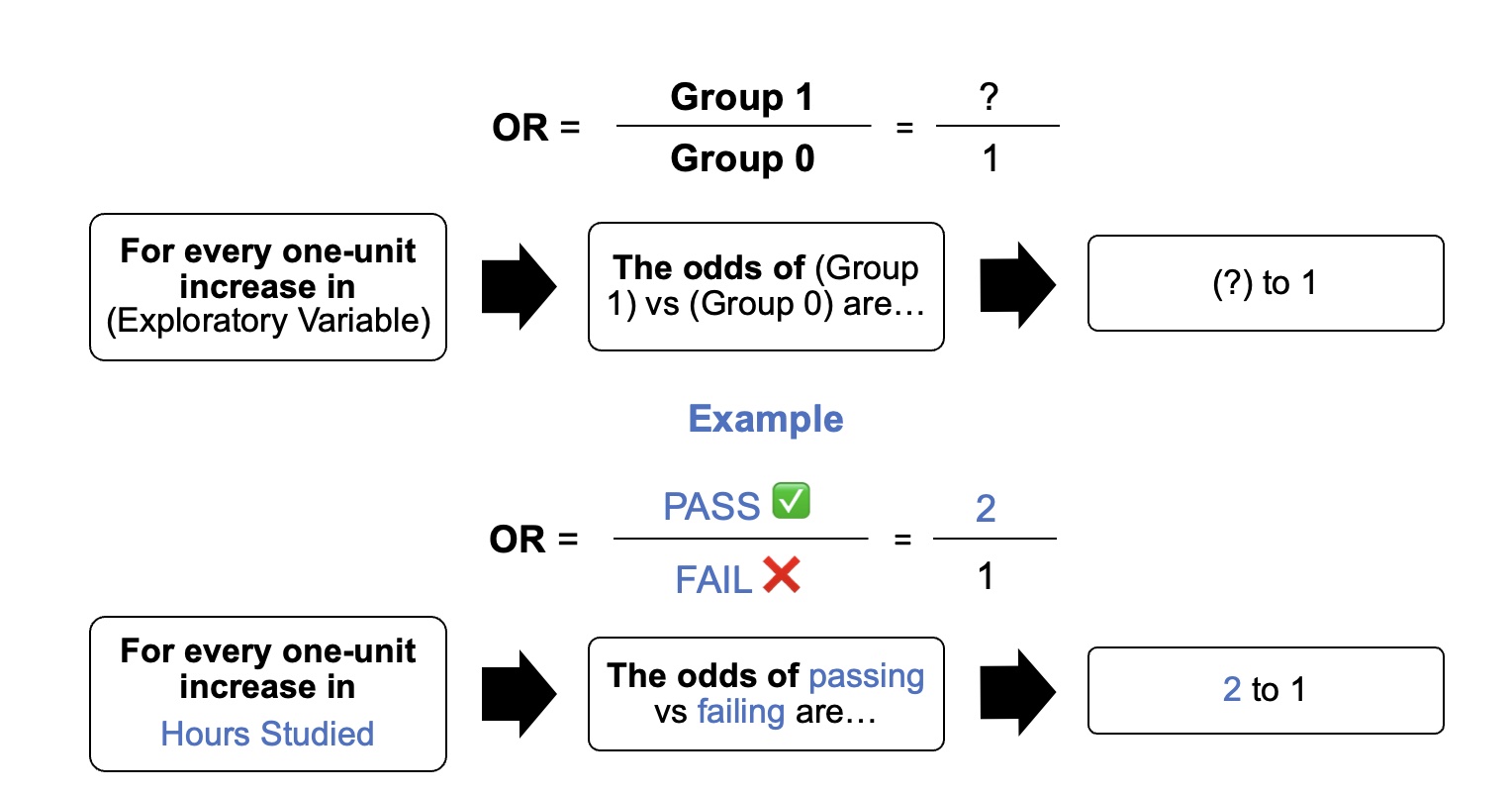
 As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
 The
The
 This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2
This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2
probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ...
of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
, logistic regression (or logit regression) is estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary dependent variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or dema ...
, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function
A logistic function or logistic curve is a common S-shaped curve (sigmoid function, sigmoid curve) with equation
f(x) = \frac,
where
For values of x in the domain of real numbers from -\infty to +\infty, the S-curve shown on the right is ...
, hence the name. The unit of measurement
A unit of measurement is a definite magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other quantity of that kind can be expressed as a mult ...
for the log-odds scale is called a '' logit'', from ''logistic unit'', hence the alternative names. See and for formal mathematics, and for a worked example.
Binary variables are widely used in statistics to model the probability of a certain class or event taking place, such as the probability of a team winning, of a patient being healthy, etc. (see ), and the logistic model has been the most commonly used model for binary regression
In statistics, specifically regression analysis, a binary regression estimates a relationship between one or more explanatory variables and a single output binary variable. Generally the probability of the two alternatives is modeled, instead of ...
since about 1970. Binary variables can be generalized to categorical variables when there are more than two possible values (e.g. whether an image is of a cat, dog, lion, etc.), and the binary logistic regression generalized to multinomial logistic regression
In statistics, multinomial logistic regression is a statistical classification, classification method that generalizes logistic regression to multiclass classification, multiclass problems, i.e. with more than two possible discrete outcomes. T ...
. If the multiple categories are ordered, one can use the ordinal logistic regression
In statistics, the ordered logit model (also ordered logistic regression or proportional odds model) is an ordinal regression model—that is, a regression model for ordinal dependent variables—first considered by Peter McCullagh. For example ...
(for example the proportional odds ordinal logistic model). See for further extensions. The logistic regression model itself simply models probability of output in terms of input and does not perform statistical classification (it is not a classifier), though it can be used to make a classifier, for instance by choosing a cutoff value and classifying inputs with probability greater than the cutoff as one class, below the cutoff as the other; this is a common way to make a binary classifier
Binary classification is the task of classifying the elements of a set into two groups (each called ''class'') on the basis of a classification rule. Typical binary classification problems include:
* Medical testing to determine if a patient has c ...
.
Analogous linear models for binary variables with a different sigmoid function instead of the logistic function (to convert the linear combination to a probability) can also be used, most notably the probit model; see . The defining characteristic of the logistic model is that increasing one of the independent variables multiplicatively scales the odds of the given outcome at a ''constant'' rate, with each independent variable having its own parameter; for a binary dependent variable this generalizes the odds ratio. More abstractly, the logistic function is the natural parameter for the Bernoulli distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,James Victor Uspensky: ''Introduction to Mathematical Probability'', McGraw-Hill, New York 1937, page 45 is the discrete probab ...
, and in this sense is the "simplest" way to convert a real number to a probability. In particular, it maximizes entropy (minimizes added information), and in this sense makes the fewest assumptions of the data being modeled; see .
The parameters of a logistic regression are most commonly estimated by maximum-likelihood estimation (MLE). This does not have a closed-form expression, unlike linear least squares; see . Logistic regression by MLE plays a similarly basic role for binary or categorical responses as linear regression by ordinary least squares (OLS) plays for scalar responses: it is a simple, well-analyzed baseline model; see for discussion. The logistic regression as a general statistical model was originally developed and popularized primarily by Joseph Berkson, beginning in , where he coined "logit"; see .
Applications
Logistic regression is used in various fields, including machine learning, most medical fields, and social sciences. For example, the Trauma and Injury Severity Score ( TRISS), which is widely used to predict mortality in injured patients, was originally developed by Boyd ' using logistic regression. Many other medical scales used to assess severity of a patient have been developed using logistic regression. Logistic regression may be used to predict the risk of developing a given disease (e.g.diabetes
Diabetes, also known as diabetes mellitus, is a group of metabolic disorders characterized by a high blood sugar level (hyperglycemia) over a prolonged period of time. Symptoms often include frequent urination, increased thirst and increased ...
; coronary heart disease), based on observed characteristics of the patient (age, sex, body mass index, results of various blood test
A blood test is a laboratory analysis performed on a blood sample that is usually extracted from a vein in the arm using a hypodermic needle, or via fingerprick. Multiple tests for specific blood components, such as a glucose test or a ch ...
s, etc.). Another example might be to predict whether a Nepalese voter will vote Nepali Congress or Communist Party of Nepal or Any Other Party, based on age, income, sex, race, state of residence, votes in previous elections, etc. The technique can also be used in engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad rang ...
, especially for predicting the probability of failure of a given process, system or product. It is also used in marketing
Marketing is the process of exploring, creating, and delivering value to meet the needs of a target market in terms of goods and services; potentially including selection of a target audience; selection of certain attributes or themes to empha ...
applications such as prediction of a customer's propensity to purchase a product or halt a subscription, etc. In economics
Economics () is the social science that studies the production, distribution, and consumption of goods and services.
Economics focuses on the behaviour and interactions of economic agents and how economies work. Microeconomics analy ...
, it can be used to predict the likelihood of a person ending up in the labor force, and a business application would be to predict the likelihood of a homeowner defaulting on a mortgage. Conditional random fields, an extension of logistic regression to sequential data, are used in natural language processing
Natural language processing (NLP) is an interdisciplinary subfield of linguistics, computer science, and artificial intelligence concerned with the interactions between computers and human language, in particular how to program computers to proc ...
.
Example
Problem
 As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
A group of 20 students spends between 0 and 6 hours studying for an exam. How does the number of hours spent studying affect the probability of the student passing the exam?The reason for using logistic regression for this problem is that the values of the dependent variable, pass and fail, while represented by "1" and "0", are not
cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality (size) of sets. The cardinality of a finite set is a natural number: the number of elements in the set. T ...
s. If the problem was changed so that pass/fail was replaced with the grade 0–100 (cardinal numbers), then simple regression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
could be used.
The table shows the number of hours each student spent studying, and whether they passed (1) or failed (0).
We wish to fit a logistic function to the data consisting of the hours studied (''xk'') and the outcome of the test (''yk'' =1 for pass, 0 for fail). The data points are indexed by the subscript ''k'' which runs from to . The ''x'' variable is called the " explanatory variable", and the ''y'' variable is called the " categorical variable" consisting of two categories: "pass" or "fail" corresponding to the categorical values 1 and 0 respectively.
Model
logistic function
A logistic function or logistic curve is a common S-shaped curve (sigmoid function, sigmoid curve) with equation
f(x) = \frac,
where
For values of x in the domain of real numbers from -\infty to +\infty, the S-curve shown on the right is ...
is of the form:
:
where ''μ'' is a location parameter (the midpoint of the curve, where ) and ''s'' is a scale parameter. This expression may be rewritten as:
:
where and is known as the intercept (it is the ''vertical'' intercept or ''y''-intercept of the line ), and (inverse scale parameter or rate parameter): these are the ''y''-intercept and slope of the log-odds as a function of ''x''. Conversely, and .
Fit
The usual measure ofgoodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measure ...
for a logistic regression uses logistic loss (or log loss), the negative log-likelihood. For a given ''xk'' and ''yk'', write . The are the probabilities that the corresponding will be unity and are the probabilities that they will be zero (see Bernoulli distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,James Victor Uspensky: ''Introduction to Mathematical Probability'', McGraw-Hill, New York 1937, page 45 is the discrete probab ...
). We wish to find the values of and which give the "best fit" to the data. In the case of linear regression, the sum of the squared deviations of the fit from the data points (''yk''), the squared error loss
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cos ...
, is taken as a measure of the goodness of fit, and the best fit is obtained when that function is ''minimized''.
The log loss for the ''k''-th point is:
:
The log loss can be interpreted as the " surprisal" of the actual outcome relative to the prediction , and is a measure of information content. Note that log loss is always greater than or equal to 0, equals 0 only in case of a perfect prediction (i.e., when and , or and ), and approaches infinity as the prediction gets worse (i.e., when and or and ), meaning the actual outcome is "more surprising". Since the value of the logistic function is always strictly between zero and one, the log loss is always greater than zero and less than infinity. Note that unlike in a linear regression, where the model can have zero loss at a point by passing through a data point (and zero loss overall if all points are on a line), in a logistic regression it is not possible to have zero loss at any points, since is either 0 or 1, but .
These can be combined into a single expression:
:
This expression is more formally known as the cross entropy of the predicted distribution from the actual distribution , as probability distributions on the two-element space of (pass, fail).
The sum of these, the total loss, is the overall negative log-likelihood , and the best fit is obtained for those choices of and for which is ''minimized''.
Alternatively, instead of ''minimizing'' the loss, one can ''maximize'' its inverse, the (positive) log-likelihood:
:
or equivalently maximize the likelihood function itself, which is the probability that the given data set is produced by a particular logistic function:
:
This method is known as maximum likelihood estimation.
Parameter estimation
Since ''ℓ'' is nonlinear in and , determining their optimum values will require numerical methods. Note that one method of maximizing ''ℓ'' is to require the derivatives of ''ℓ'' with respect to and to be zero: : : and the maximization procedure can be accomplished by solving the above two equations for and , which, again, will generally require the use of numerical methods. The values of and which maximize ''ℓ'' and ''L'' using the above data are found to be: : : which yields a value for ''μ'' and ''s'' of: : :Predictions
The and coefficients may be entered into the logistic regression equation to estimate the probability of passing the exam. For example, for a student who studies 2 hours, entering the value into the equation gives the estimated probability of passing the exam of 0.25: : : Similarly, for a student who studies 4 hours, the estimated probability of passing the exam is 0.87: : : This table shows the estimated probability of passing the exam for several values of hours studying.Model evaluation
The logistic regression analysis gives the following output. By the Wald test, the output indicates that hours studying is significantly associated with the probability of passing the exam (). Rather than the Wald method, the recommended method to calculate the ''p''-value for logistic regression is the likelihood-ratio test (LRT), which for this data gives (see below).Generalizations
This simple model is an example of binary logistic regression, and has one explanatory variable and a binary categorical variable which can assume one of two categorical values.Multinomial logistic regression
In statistics, multinomial logistic regression is a statistical classification, classification method that generalizes logistic regression to multiclass classification, multiclass problems, i.e. with more than two possible discrete outcomes. T ...
is the generalization of binary logistic regression to include any number of explanatory variables and any number of categories.
Background
Definition of the logistic function
An explanation of logistic regression can begin with an explanation of the standardlogistic function
A logistic function or logistic curve is a common S-shaped curve (sigmoid function, sigmoid curve) with equation
f(x) = \frac,
where
For values of x in the domain of real numbers from -\infty to +\infty, the S-curve shown on the right is ...
. The logistic function is a sigmoid function, which takes any real input , and outputs a value between zero and one. For the logit, this is interpreted as taking input log-odds and having output probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ...
. The ''standard'' logistic function is defined as follows:
:
A graph of the logistic function on the ''t''-interval (−6,6) is shown in Figure 1.
Let us assume that is a linear function of a single explanatory variable (the case where is a ''linear combination'' of multiple explanatory variables is treated similarly). We can then express as follows:
:
And the general logistic function can now be written as:
:
In the logistic model, is interpreted as the probability of the dependent variable equaling a success/case rather than a failure/non-case. It's clear that the response variables are not identically distributed: differs from one data point to another, though they are independent given design matrix and shared parameters .
Definition of the inverse of the logistic function
We can now define the logit (log odds) function as the inverse of the standard logistic function. It is easy to see that it satisfies: : and equivalently, after exponentiating both sides we have the odds: :Interpretation of these terms
In the above equations, the terms are as follows: * is the logit function. The equation for illustrates that the logit (i.e., log-odds or natural logarithm of the odds) is equivalent to the linear regression expression. * denotes thenatural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
.
* is the probability that the dependent variable equals a case, given some linear combination of the predictors. The formula for illustrates that the probability of the dependent variable equaling a case is equal to the value of the logistic function of the linear regression expression. This is important in that it shows that the value of the linear regression expression can vary from negative to positive infinity and yet, after transformation, the resulting expression for the probability ranges between 0 and 1.
* is the intercept from the linear regression equation (the value of the criterion when the predictor is equal to zero).
* is the regression coefficient multiplied by some value of the predictor.
* base denotes the exponential function.
Definition of the odds
The odds of the dependent variable equaling a case (given some linear combination of the predictors) is equivalent to the exponential function of the linear regression expression. This illustrates how the logit serves as a link function between the probability and the linear regression expression. Given that the logit ranges between negative and positive infinity, it provides an adequate criterion upon which to conduct linear regression and the logit is easily converted back into the odds. So we define odds of the dependent variable equaling a case (given some linear combination of the predictors) as follows: :The odds ratio
For a continuous independent variable the odds ratio can be defined as: : This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2
This exponential relationship provides an interpretation for : The odds multiply by for every 1-unit increase in x.
For a binary independent variable the odds ratio is defined as where ''a'', ''b'', ''c'' and ''d'' are cells in a 2×2 contingency table
In statistics, a contingency table (also known as a cross tabulation or crosstab) is a type of table in a matrix format that displays the (multivariate) frequency distribution of the variables. They are heavily used in survey research, business ...
.
Multiple explanatory variables
If there are multiple explanatory variables, the above expression can be revised to . Then when this is used in the equation relating the log odds of a success to the values of the predictors, the linear regression will be a multiple regression with ''m'' explanators; the parameters for all are all estimated. Again, the more traditional equations are: : and : where usually .Definition
The basic setup of logistic regression is as follows. We are given a dataset containing ''N'' points. Each point ''i'' consists of a set of ''m'' input variables ''x''1,''i'' ... ''x''''m,i'' (also called independent variables, explanatory variables, predictor variables, features, or attributes), and a binary outcome variable ''Y''''i'' (also known as adependent variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or dema ...
, response variable, output variable, or class), i.e. it can assume only the two possible values 0 (often meaning "no" or "failure") or 1 (often meaning "yes" or "success"). The goal of logistic regression is to use the dataset to create a predictive model of the outcome variable.
As in linear regression, the outcome variables ''Y''''i'' are assumed to depend on the explanatory variables ''x''1,''i'' ... ''x''''m,i''.
; Explanatory variables
The explanatory variables may be of any type
Type may refer to:
Science and technology Computing
* Typing, producing text via a keyboard, typewriter, etc.
* Data type, collection of values used for computations.
* File type
* TYPE (DOS command), a command to display contents of a file.
* Ty ...
: real-valued, binary, categorical, etc. The main distinction is between continuous variables and discrete variables.
(Discrete variables referring to more than two possible choices are typically coded using dummy variables (or indicator variables), that is, separate explanatory variables taking the value 0 or 1 are created for each possible value of the discrete variable, with a 1 meaning "variable does have the given value" and a 0 meaning "variable does not have that value".)
;Outcome variables
Formally, the outcomes ''Y''''i'' are described as being Bernoulli-distributed data, where each outcome is determined by an unobserved probability ''p''''i'' that is specific to the outcome at hand, but related to the explanatory variables. This can be expressed in any of the following equivalent forms:
::
The meanings of these four lines are:
# The first line expresses the probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomeno ...
of each ''Y''''i'' : conditioned on the explanatory variables, it follows a Bernoulli distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,James Victor Uspensky: ''Introduction to Mathematical Probability'', McGraw-Hill, New York 1937, page 45 is the discrete probab ...
with parameters ''p''''i'', the probability of the outcome of 1 for trial ''i''. As noted above, each separate trial has its own probability of success, just as each trial has its own explanatory variables. The probability of success ''p''''i'' is not observed, only the outcome of an individual Bernoulli trial using that probability.
# The second line expresses the fact that the expected value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a ...
of each ''Y''''i'' is equal to the probability of success ''p''''i'', which is a general property of the Bernoulli distribution. In other words, if we run a large number of Bernoulli trials using the same probability of success ''p''''i'', then take the average of all the 1 and 0 outcomes, then the result would be close to ''p''''i''. This is because doing an average this way simply computes the proportion of successes seen, which we expect to converge to the underlying probability of success.
# The third line writes out the probability mass function of the Bernoulli distribution, specifying the probability of seeing each of the two possible outcomes.
# The fourth line is another way of writing the probability mass function, which avoids having to write separate cases and is more convenient for certain types of calculations. This relies on the fact that ''Y''''i'' can take only the value 0 or 1. In each case, one of the exponents will be 1, "choosing" the value under it, while the other is 0, "canceling out" the value under it. Hence, the outcome is either ''p''''i'' or 1 − ''p''''i'', as in the previous line.
; Linear predictor function
The basic idea of logistic regression is to use the mechanism already developed for linear regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is ...
by modeling the probability ''p''''i'' using a linear predictor function, i.e. a linear combination of the explanatory variables and a set of regression coefficients that are specific to the model at hand but the same for all trials. The linear predictor function for a particular data point ''i'' is written as:
:
where are regression coefficients indicating the relative effect of a particular explanatory variable on the outcome.
The model is usually put into a more compact form as follows:
* The regression coefficients ''β''0, ''β''1, ..., ''β''''m'' are grouped into a single vector ''β'' of size ''m'' + 1.
* For each data point ''i'', an additional explanatory pseudo-variable ''x''0,''i'' is added, with a fixed value of 1, corresponding to the intercept coefficient ''β''0.
* The resulting explanatory variables ''x''0,''i'', ''x''1,''i'', ..., ''x''''m,i'' are then grouped into a single vector ''Xi'' of size ''m'' + 1.
This makes it possible to write the linear predictor function as follows:
:
using the notation for a dot product between two vectors.
Many explanatory variables, two categories
The above example of binary logistic regression on one explanatory variable can be generalized to binary logistic regression on any number of explanatory variables ''x1, x2,...'' and any number of categorical values . To begin with, we may consider a logistic model with ''M'' explanatory variables, ''x1'', ''x2'' ... ''xM'' and, as in the example above, two categorical values (''y'' = 0 and 1). For the simple binary logistic regression model, we assumed a linear relationship between the predictor variable and the log-odds (also called logit) of the event that . This linear relationship may be extended to the case of ''M'' explanatory variables: : where ''t'' is the log-odds and are parameters of the model. An additional generalization has been introduced in which the base of the model (''b'') is not restricted to the Euler number ''e''. In most applications, the base of the logarithm is usually taken to be '' e''. However, in some cases it can be easier to communicate results by working in base 2 or base 10. For a more compact notation, we will specify the explanatory variables and the ''β'' coefficients as -dimensional vectors: : : with an added explanatory variable ''x0'' =1. The logit may now be written as: : Solving for the probability ''p'' that yields: :, where is the sigmoid function with base . The above formula shows that once the are fixed, we can easily compute either the log-odds that for a given observation, or the probability that for a given observation. The main use-case of a logistic model is to be given an observation x, and estimate the probability ''p(x)'' that . The optimum beta coefficients may again be found by maximizing the log-likelihood. For ''K'' measurements, defining xk as the explanatory vector of the ''k''-th measurement, and ''y''k as the categorical outcome of that measurement, the log likelihood may be written in a form very similar to the simple case above: : As in the simple example above, finding the optimum ''β'' parameters will require numerical methods. One useful technique is to equate the derivatives of the log likelihood with respect to each of the ''β'' parameters to zero yielding a set of equations which will hold at the maximum of the log likelihood: : where ''xmk'' is the value of the ''xm'' explanatory variable from the ''k-th'' measurement. Consider an example with explanatory variables, , and coefficients , , and which have been determined by the above method. To be concrete, the model is: : :, where ''p'' is the probability of the event that . This can be interpreted as follows: * is the ''y''-intercept. It is the log-odds of the event that , when the predictors . By exponentiating, we can see that when the odds of the event that are 1-to-1000, or . Similarly, the probability of the event that when can be computed as * means that increasing by 1 increases the log-odds by . So if increases by 1, the odds that increase by a factor of . Note that the probability of has also increased, but it has not increased by as much as the odds have increased. * means that increasing by 1 increases the log-odds by . So if increases by 1, the odds that increase by a factor of Note how the effect of on the log-odds is twice as great as the effect of , but the effect on the odds is 10 times greater. But the effect on the probability of is not as much as 10 times greater, it's only the effect on the odds that is 10 times greater.Multinomial logistic regression: Many explanatory variables and many categories
In the above cases of two categories (binomial logistic regression), the categories were indexed by "0" and "1", and we had two probability distributions: The probability that the outcome was in category 1 was given by and the probability that the outcome was in category 0 was given by . The sum of both probabilities is equal to unity, as they must be. In general, if we have explanatory variables (including ''x0'') and categories, we will need separate probability distributions, one for each category, indexed by ''n'', which describe the probability that the categorical outcome ''y'' for explanatory vector x will be in category ''y=n''. It will also be required that the sum of these probabilities over all categories be equal to unity. Using the mathematically convenient base ''e'', these probabilities are: : for : Each of the probabilities except will have their own set of regression coefficients . It can be seen that, as required, the sum of the over all categories is unity. Note that the selection of to be defined in terms of the other probabilities is artificial. Any of the probabilities could have been selected to be so defined. This special value of ''n'' is termed the "pivot index", and the log-odds (''tn'') are expressed in terms of the pivot probability and are again expressed as a linear combination of the explanatory variables: : Note also that for the simple case of , the two-category case is recovered, with and . The log-likelihood that a particular set of ''K'' measurements or data points will be generated by the above probabilities can now be calculated. Indexing each measurement by ''k'', let the ''k''-th set of measured explanatory variables be denoted by and their categorical outcomes be denoted by which can be equal to any integer in ,N The log-likelihood is then: : where is anindicator function
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , one has \mathbf_(x)=1 if x ...
which is equal to unity if ''yk = n'' and zero otherwise. In the case of two explanatory variables, this indicator function was defined as ''yk'' when ''n'' = 1 and ''1-yk'' when ''n'' = 0. This was convenient, but not necessary. Again, the optimum beta coefficients may be found by maximizing the log-likelihood function generally using numerical methods. A possible method of solution is to set the derivatives of the log-likelihood with respect to each beta coefficient equal to zero and solve for the beta coefficients:
:
where is the ''m''-th coefficient of the vector and is the ''m''-th explanatory variable of the ''k''-th measurement. Once the beta coefficients have been estimated from the data, we will be able to estimate the probability that any subsequent set of explanatory variables will result in any of the possible outcome categories.
Interpretations
There are various equivalent specifications and interpretations of logistic regression, which fit into different types of more general models, and allow different generalizations.As a generalized linear model
The particular model used by logistic regression, which distinguishes it from standardlinear regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is ...
and from other types of regression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
used for binary-valued
Binary data is data whose unit can take on only two possible states. These are often labelled as 0 and 1 in accordance with the binary numeral system and Boolean algebra.
Binary data occurs in many different technical and scientific fields, wher ...
outcomes, is the way the probability of a particular outcome is linked to the linear predictor function:
:
Written using the more compact notation described above, this is:
:
This formulation expresses logistic regression as a type of generalized linear model, which predicts variables with various types of probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomeno ...
s by fitting a linear predictor function of the above form to some sort of arbitrary transformation of the expected value of the variable.
The intuition for transforming using the logit function (the natural log of the odds) was explained above. It also has the practical effect of converting the probability (which is bounded to be between 0 and 1) to a variable that ranges over — thereby matching the potential range of the linear prediction function on the right side of the equation.
Note that both the probabilities ''p''''i'' and the regression coefficients are unobserved, and the means of determining them is not part of the model itself. They are typically determined by some sort of optimization procedure, e.g. maximum likelihood estimation, that finds values that best fit the observed data (i.e. that give the most accurate predictions for the data already observed), usually subject to regularization conditions that seek to exclude unlikely values, e.g. extremely large values for any of the regression coefficients. The use of a regularization condition is equivalent to doing maximum a posteriori (MAP) estimation, an extension of maximum likelihood. (Regularization is most commonly done using a squared regularizing function, which is equivalent to placing a zero-mean Gaussian prior distribution on the coefficients, but other regularizers are also possible.) Whether or not regularization is used, it is usually not possible to find a closed-form solution; instead, an iterative numerical method must be used, such as iteratively reweighted least squares
The method of iteratively reweighted least squares (IRLS) is used to solve certain optimization problems with objective functions of the form of a ''p''-norm:
:\underset \sum_^n \big, y_i - f_i (\boldsymbol\beta) \big, ^p,
by an iterative m ...
(IRLS) or, more commonly these days, a quasi-Newton method such as the L-BFGS method.
The interpretation of the ''β''''j'' parameter estimates is as the additive effect on the log of the odds for a unit change in the ''j'' the explanatory variable. In the case of a dichotomous explanatory variable, for instance, gender is the estimate of the odds of having the outcome for, say, males compared with females.
An equivalent formula uses the inverse of the logit function, which is the logistic function
A logistic function or logistic curve is a common S-shaped curve (sigmoid function, sigmoid curve) with equation
f(x) = \frac,
where
For values of x in the domain of real numbers from -\infty to +\infty, the S-curve shown on the right is ...
, i.e.:
:
The formula can also be written as a probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomeno ...
(specifically, using a probability mass function):
:
As a latent-variable model
The logistic model has an equivalent formulation as a latent-variable model. This formulation is common in the theory ofdiscrete choice
In economics, discrete choice models, or qualitative choice models, describe, explain, and predict choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Su ...
models and makes it easier to extend to certain more complicated models with multiple, correlated choices, as well as to compare logistic regression to the closely related probit model.
Imagine that, for each trial ''i'', there is a continuous latent variable ''Y''''i''* (i.e. an unobserved random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the p ...
) that is distributed as follows:
:
where
:
i.e. the latent variable can be written directly in terms of the linear predictor function and an additive random error variable that is distributed according to a standard logistic distribution.
Then ''Y''''i'' can be viewed as an indicator for whether this latent variable is positive:
:
The choice of modeling the error variable specifically with a standard logistic distribution, rather than a general logistic distribution with the location and scale set to arbitrary values, seems restrictive, but in fact, it is not. It must be kept in mind that we can choose the regression coefficients ourselves, and very often can use them to offset changes in the parameters of the error variable's distribution. For example, a logistic error-variable distribution with a non-zero location parameter ''μ'' (which sets the mean) is equivalent to a distribution with a zero location parameter, where ''μ'' has been added to the intercept coefficient. Both situations produce the same value for ''Y''''i''* regardless of settings of explanatory variables. Similarly, an arbitrary scale parameter ''s'' is equivalent to setting the scale parameter to 1 and then dividing all regression coefficients by ''s''. In the latter case, the resulting value of ''Y''''i''''*'' will be smaller by a factor of ''s'' than in the former case, for all sets of explanatory variables — but critically, it will always remain on the same side of 0, and hence lead to the same ''Y''''i'' choice.
(Note that this predicts that the irrelevancy of the scale parameter may not carry over into more complex models where more than two choices are available.)
It turns out that this formulation is exactly equivalent to the preceding one, phrased in terms of the generalized linear model and without any latent variables. This can be shown as follows, using the fact that the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
(CDF) of the standard logistic distribution is the logistic function
A logistic function or logistic curve is a common S-shaped curve (sigmoid function, sigmoid curve) with equation
f(x) = \frac,
where
For values of x in the domain of real numbers from -\infty to +\infty, the S-curve shown on the right is ...
, which is the inverse of the logit function, i.e.
:
Then:
:
This formulation—which is standard in discrete choice
In economics, discrete choice models, or qualitative choice models, describe, explain, and predict choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Su ...
models—makes clear the relationship between logistic regression (the "logit model") and the probit model, which uses an error variable distributed according to a standard normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu i ...
instead of a standard logistic distribution. Both the logistic and normal distributions are symmetric with a basic unimodal, "bell curve" shape. The only difference is that the logistic distribution has somewhat heavier tails, which means that it is less sensitive to outlying data (and hence somewhat more robust to model mis-specifications or erroneous data).
Two-way latent-variable model
Yet another formulation uses two separate latent variables: : where : where ''EV''1(0,1) is a standard type-1 extreme value distribution: i.e. : Then : This model has a separate latent variable and a separate set of regression coefficients for each possible outcome of the dependent variable. The reason for this separation is that it makes it easy to extend logistic regression to multi-outcome categorical variables, as in the multinomial logit model. In such a model, it is natural to model each possible outcome using a different set of regression coefficients. It is also possible to motivate each of the separate latent variables as the theoreticalutility
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosoph ...
associated with making the associated choice, and thus motivate logistic regression in terms of utility theory. (In terms of utility theory, a rational actor always chooses the choice with the greatest associated utility.) This is the approach taken by economists when formulating discrete choice
In economics, discrete choice models, or qualitative choice models, describe, explain, and predict choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Su ...
models, because it both provides a theoretically strong foundation and facilitates intuitions about the model, which in turn makes it easy to consider various sorts of extensions. (See the example below.)
The choice of the type-1 extreme value distribution seems fairly arbitrary, but it makes the mathematics work out, and it may be possible to justify its use through rational choice theory.
It turns out that this model is equivalent to the previous model, although this seems non-obvious, since there are now two sets of regression coefficients and error variables, and the error variables have a different distribution. In fact, this model reduces directly to the previous one with the following substitutions:
:
:
An intuition for this comes from the fact that, since we choose based on the maximum of two values, only their difference matters, not the exact values — and this effectively removes one degree of freedom. Another critical fact is that the difference of two type-1 extreme-value-distributed variables is a logistic distribution, i.e. We can demonstrate the equivalent as follows:
:
Example
: As an example, consider a province-level election where the choice is between a right-of-center party, a left-of-center party, and a secessionist party (e.g. theParti Québécois
The Parti Québécois (; ; PQ) is a Quebec sovereignty movement, sovereignist and social democracy, social democratic provincial list of political parties in Quebec, political party in Quebec, Canada. The PQ advocates Quebec sovereignty movement ...
, which wants Quebec
Quebec ( ; )According to the Government of Canada, Canadian government, ''Québec'' (with the acute accent) is the official name in Canadian French and ''Quebec'' (without the accent) is the province's official name in Canadian English is ...
to secede from Canada
Canada is a country in North America. Its ten provinces and three territories extend from the Atlantic Ocean to the Pacific Ocean and northward into the Arctic Ocean, covering over , making it the world's second-largest country by tota ...
). We would then use three latent variables, one for each choice. Then, in accordance with utility theory, we can then interpret the latent variables as expressing the utility
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosoph ...
that results from making each of the choices. We can also interpret the regression coefficients as indicating the strength that the associated factor (i.e. explanatory variable) has in contributing to the utility — or more correctly, the amount by which a unit change in an explanatory variable changes the utility of a given choice. A voter might expect that the right-of-center party would lower taxes, especially on rich people. This would give low-income people no benefit, i.e. no change in utility (since they usually don't pay taxes); would cause moderate benefit (i.e. somewhat more money, or moderate utility increase) for middle-incoming people; would cause significant benefits for high-income people. On the other hand, the left-of-center party might be expected to raise taxes and offset it with increased welfare and other assistance for the lower and middle classes. This would cause significant positive benefit to low-income people, perhaps a weak benefit to middle-income people, and significant negative benefit to high-income people. Finally, the secessionist party would take no direct actions on the economy, but simply secede. A low-income or middle-income voter might expect basically no clear utility gain or loss from this, but a high-income voter might expect negative utility since he/she is likely to own companies, which will have a harder time doing business in such an environment and probably lose money.
These intuitions can be expressed as follows:
This clearly shows that
# Separate sets of regression coefficients need to exist for each choice. When phrased in terms of utility, this can be seen very easily. Different choices have different effects on net utility; furthermore, the effects vary in complex ways that depend on the characteristics of each individual, so there need to be separate sets of coefficients for each characteristic, not simply a single extra per-choice characteristic.
# Even though income is a continuous variable, its effect on utility is too complex for it to be treated as a single variable. Either it needs to be directly split up into ranges, or higher powers of income need to be added so that polynomial regression
In statistics, polynomial regression is a form of regression analysis in which the relationship between the independent variable ''x'' and the dependent variable ''y'' is modelled as an ''n''th degree polynomial in ''x''. Polynomial regression fi ...
on income is effectively done.
As a "log-linear" model
Yet another formulation combines the two-way latent variable formulation above with the original formulation higher up without latent variables, and in the process provides a link to one of the standard formulations of the multinomial logit. Here, instead of writing the logit of the probabilities ''p''''i'' as a linear predictor, we separate the linear predictor into two, one for each of the two outcomes: : Two separate sets of regression coefficients have been introduced, just as in the two-way latent variable model, and the two equations appear a form that writes thelogarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of ...
of the associated probability as a linear predictor, with an extra term at the end. This term, as it turns out, serves as the normalizing factor ensuring that the result is a distribution. This can be seen by exponentiating both sides:
:
In this form it is clear that the purpose of ''Z'' is to ensure that the resulting distribution over ''Y''''i'' is in fact a probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomeno ...
, i.e. it sums to 1. This means that ''Z'' is simply the sum of all un-normalized probabilities, and by dividing each probability by ''Z'', the probabilities become " normalized". That is:
:
and the resulting equations are
:
Or generally:
:
This shows clearly how to generalize this formulation to more than two outcomes, as in multinomial logit.
Note that this general formulation is exactly the softmax function as in
:
In order to prove that this is equivalent to the previous model, note that the above model is overspecified, in that and cannot be independently specified: rather so knowing one automatically determines the other. As a result, the model is nonidentifiable
In statistics, identifiability is a property which a model must satisfy for precise inference to be possible. A model is identifiable if it is theoretically possible to learn the true values of this model's underlying parameters after obtaining an ...
, in that multiple combinations of ''β''0 and ''β''1 will produce the same probabilities for all possible explanatory variables. In fact, it can be seen that adding any constant vector to both of them will produce the same probabilities:
:
As a result, we can simplify matters, and restore identifiability, by picking an arbitrary value for one of the two vectors. We choose to set Then,
:
and so
:
which shows that this formulation is indeed equivalent to the previous formulation. (As in the two-way latent variable formulation, any settings where will produce equivalent results.)
Note that most treatments of the multinomial logit model start out either by extending the "log-linear" formulation presented here or the two-way latent variable formulation presented above, since both clearly show the way that the model could be extended to multi-way outcomes. In general, the presentation with latent variables is more common in econometrics
Econometrics is the application of statistical methods to economic data in order to give empirical content to economic relationships.M. Hashem Pesaran (1987). "Econometrics," '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8� ...
and political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and power, and the analysis of political activities, political thought, political behavior, and associated constitutions and ...
, where discrete choice
In economics, discrete choice models, or qualitative choice models, describe, explain, and predict choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Su ...
models and utility theory reign, while the "log-linear" formulation here is more common in computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
, e.g. machine learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence.
Machine ...
and natural language processing
Natural language processing (NLP) is an interdisciplinary subfield of linguistics, computer science, and artificial intelligence concerned with the interactions between computers and human language, in particular how to program computers to proc ...
.
As a single-layer perceptron
The model has an equivalent formulation : This functional form is commonly called a single-layer perceptron or single-layerartificial neural network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected units ...
. A single-layer neural network computes a continuous output instead of a step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having on ...
. The derivative of ''pi'' with respect to ''X'' = (''x''1, ..., ''x''''k'') is computed from the general form:
:
where ''f''(''X'') is an analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex ...
in ''X''. With this choice, the single-layer neural network is identical to the logistic regression model. This function has a continuous derivative, which allows it to be used in backpropagation. This function is also preferred because its derivative is easily calculated:
:
In terms of binomial data
A closely related model assumes that each ''i'' is associated not with a single Bernoulli trial but with ''n''''i'' independent identically distributed trials, where the observation ''Y''''i'' is the number of successes observed (the sum of the individual Bernoulli-distributed random variables), and hence follows abinomial distribution
In probability theory and statistics, the binomial distribution with parameters ''n'' and ''p'' is the discrete probability distribution of the number of successes in a sequence of ''n'' independent experiments, each asking a yes–no qu ...
:
:
An example of this distribution is the fraction of seeds (''p''''i'') that germinate after ''n''''i'' are planted.
In terms of expected value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a ...
s, this model is expressed as follows:
:
so that
:
Or equivalently:
:
This model can be fit using the same sorts of methods as the above more basic model.
Model fitting
Maximum likelihood estimation (MLE)
The regression coefficients are usually estimated using maximum likelihood estimation. Unlike linear regression with normally distributed residuals, it is not possible to find a closed-form expression for the coefficient values that maximize the likelihood function, so that an iterative process must be used instead; for exampleNewton's method
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real ...
. This process begins with a tentative solution, revises it slightly to see if it can be improved, and repeats this revision until no more improvement is made, at which point the process is said to have converged.
In some instances, the model may not reach convergence. Non-convergence of a model indicates that the coefficients are not meaningful because the iterative process was unable to find appropriate solutions. A failure to converge may occur for a number of reasons: having a large ratio of predictors to cases, multicollinearity, sparseness, or complete separation
Separation may refer to:
Films
* ''Separation'' (1967 film), a British feature film written by and starring Jane Arden and directed by Jack Bond
* ''La Séparation'', 1994 French film
* ''A Separation'', 2011 Iranian film
* ''Separation'' (20 ...
.
* Having a large ratio of variables to cases results in an overly conservative Wald statistic (discussed below) and can lead to non-convergence. Regularized logistic regression is specifically intended to be used in this situation.
* Multicollinearity refers to unacceptably high correlations between predictors. As multicollinearity increases, coefficients remain unbiased but standard errors increase and the likelihood of model convergence decreases. To detect multicollinearity amongst the predictors, one can conduct a linear regression analysis with the predictors of interest for the sole purpose of examining the tolerance statistic used to assess whether multicollinearity is unacceptably high.
* Sparseness in the data refers to having a large proportion of empty cells (cells with zero counts). Zero cell counts are particularly problematic with categorical predictors. With continuous predictors, the model can infer values for the zero cell counts, but this is not the case with categorical predictors. The model will not converge with zero cell counts for categorical predictors because the natural logarithm of zero is an undefined value so that the final solution to the model cannot be reached. To remedy this problem, researchers may collapse categories in a theoretically meaningful way or add a constant to all cells.
* Another numerical problem that may lead to a lack of convergence is complete separation, which refers to the instance in which the predictors perfectly predict the criterion – all cases are accurately classified and the likelihood maximized with infinite coefficients. In such instances, one should re-examine the data, as there may be some kind of error.
* One can also take semi-parametric or non-parametric approaches, e.g., via local-likelihood or nonparametric quasi-likelihood methods, which avoid assumptions of a parametric form for the index function and is robust to the choice of the link function (e.g., probit or logit).
Iteratively reweighted least squares (IRLS)
Binary logistic regression ( or ) can, for example, be calculated using ''iteratively reweighted least squares'' (IRLS), which is equivalent to maximizing the log-likelihood of a Bernoulli distributed process usingNewton's method
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real ...
. If the problem is written in vector matrix form, with parameters