|
Regularization (mathematics)
In mathematics, statistics, Mathematical finance, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the Problem solving, answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be Prior probability, priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Regularization
Regularization may refer to: * Regularization (linguistics) * Regularization (mathematics) * Regularization (physics) * Regularization (solid modeling) * Regularization Law, an Israeli law intended to retroactively legalize settlements See also * Matrix regularization {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
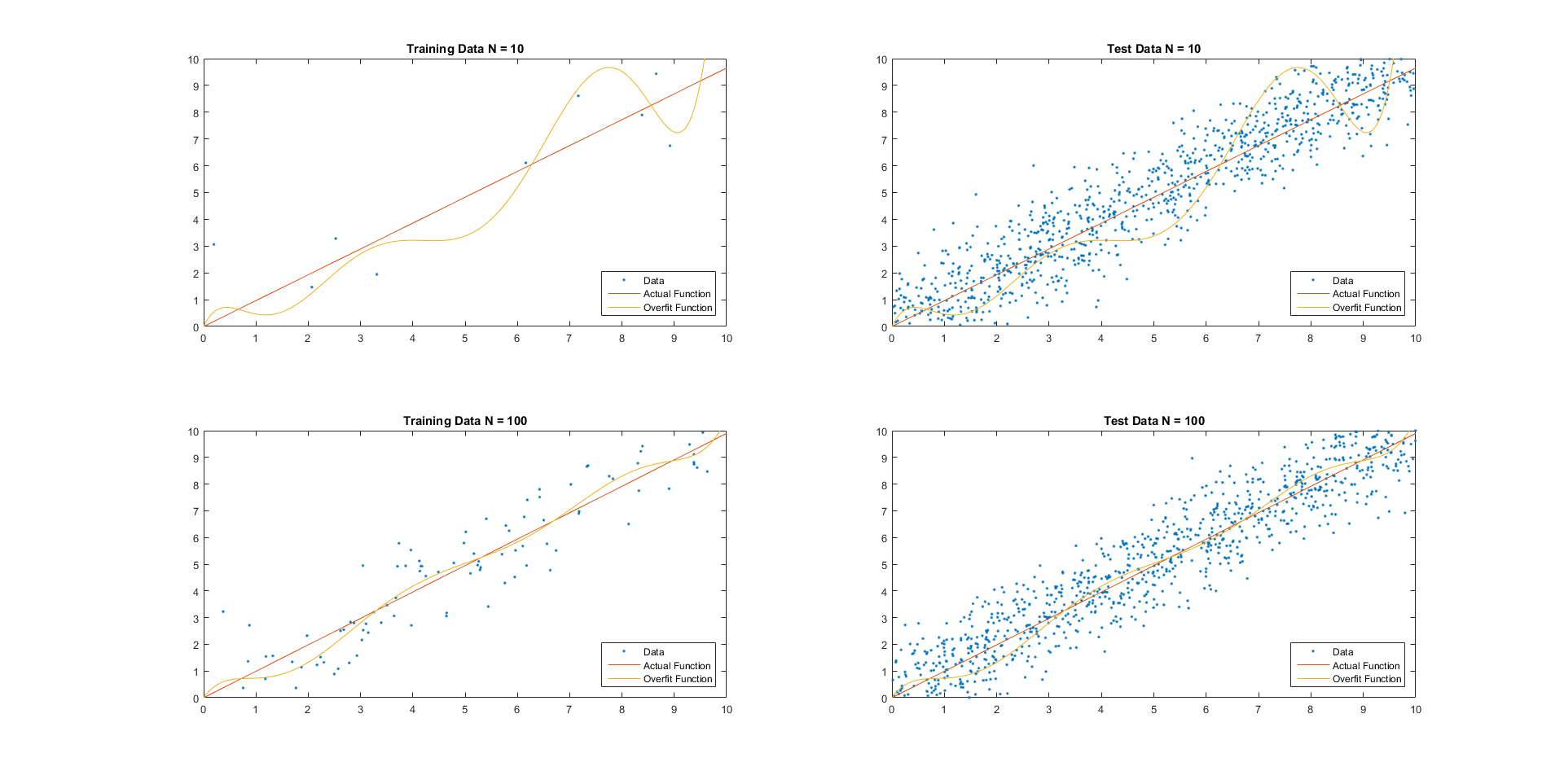
Generalization Error
For supervised learning applications in machine learning and statistical learning theory, generalization errorMohri, M., Rostamizadeh A., Talwakar A., (2018) ''Foundations of Machine learning'', 2nd ed., Boston: MIT Press (also known as the out-of-sample errorY S. Abu-Mostafa, M.Magdon-Ismail, and H.-T. Lin (2012) Learning from Data, AMLBook Press. or the risk) is a measure of how accurately an algorithm is able to predict outcomes for previously unseen data. As learning algorithms are evaluated on finite samples, the evaluation of a learning algorithm may be sensitive to sampling error. As a result, measurements of prediction error on the current data may not provide much information about the algorithm's predictive ability on new, unseen data. The generalization error can be minimized by avoiding overfitting in the learning algorithm. The performance of machine learning algorithms is commonly visualized by Learning curve (machine learning), learning curve plots that show estimates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Occam's Razor
In philosophy, Occam's razor (also spelled Ockham's razor or Ocham's razor; ) is the problem-solving principle that recommends searching for explanations constructed with the smallest possible set of elements. It is also known as the principle of parsimony or the law of parsimony (). Attributed to William of Ockham, a 14th-century English philosopher and theologian, it is frequently cited as , which translates as "Entities must not be multiplied beyond necessity", although Occam never used these exact words. Popularly, the principle is sometimes paraphrased as "of two competing theories, the simpler explanation of an entity is to be preferred." This philosophical razor advocates that when presented with competing hypotheses about the same prediction and both hypotheses have equal explanatory power, one should prefer the hypothesis that requires the fewest assumptions, and that this is not meant to be a way of choosing between hypotheses that make different predictions. Similarl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Normed Vector Space
The Ateliers et Chantiers de France (ACF, Workshops and Shipyards of France) was a major shipyard that was established in Dunkirk, France, in 1898. The shipyard boomed in the period before World War I (1914–18), but struggled in the inter-war period. It was badly damaged during World War II (1939–45). In the first thirty years after the war the shipyard again experienced a boom and employed up to 3,000 workers making oil tankers, and then liquid natural gas tankers. Demand dropped off in the 1970s and 1980s. In 1972 the shipyard became Chantiers de France-Dunkerque, and in 1983 merged with others yards to become part of Chantiers du Nord et de la Mediterranee, or Normed. The shipyard closed in 1987. Foundation (1898–99) The Ateliers et Chantiers de France (ACF) company was officially founded on 6 July 1898 by a consortium of six shipping brokers, the Dunkirk chamber of commerce and the state. The state asked that the shipyard be able to build steamships and also four-maste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Smooth Function
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives (''differentiability class)'' it has over its domain. A function of class C^k is a function of smoothness at least ; that is, a function of class C^k is a function that has a th derivative that is continuous in its domain. A function of class C^\infty or C^\infty-function (pronounced C-infinity function) is an infinitely differentiable function, that is, a function that has derivatives of all orders (this implies that all these derivatives are continuous). Generally, the term smooth function refers to a C^-function. However, it may also mean "sufficiently differentiable" for the problem under consideration. Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hinge Loss
In machine learning, the hinge loss is a loss function used for training classifiers. The hinge loss is used for "maximum-margin" classification, most notably for support vector machines (SVMs). For an intended output and a classifier score , the hinge loss of the prediction is defined as :\ell(y) = \max(0, 1-t \cdot y) Note that y should be the "raw" output of the classifier's decision function, not the predicted class label. For instance, in linear SVMs, y = \mathbf \cdot \mathbf + b, where (\mathbf,b) are the parameters of the hyperplane and \mathbf is the input variable(s). When and have the same sign (meaning predicts the right class) and , y, \ge 1, the hinge loss \ell(y) = 0. When they have opposite signs, \ell(y) increases linearly with , and similarly if , y, < 1, even if it has the same sign (correct prediction, but not by enough margin). Extensions While binary SVMs are commonly extended to[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Loss Functions For Classification
In machine learning and mathematical optimization, loss functions for classification are computationally feasible loss functions representing the price paid for inaccuracy of predictions in classification problems (problems of identifying which category a particular observation belongs to). Given \mathcal as the space of all possible inputs (usually \mathcal \subset \mathbb^d), and \mathcal = \ as the set of labels (possible outputs), a typical goal of classification algorithms is to find a function f: \mathcal \to \mathcal which best predicts a label y for a given input \vec. However, because of incomplete information, noise in the measurement, or probabilistic components in the underlying process, it is possible for the same \vec to generate different y. As a result, the goal of the learning problem is to minimize expected loss (also known as the risk), defined as :I = \displaystyle \int_ V(f(\vec),y) \, p(\vec,y) \, d\vec \, dy where V(f(\vec),y) is a given loss function, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Underdetermination
In the philosophy of science, underdetermination or the underdetermination of theory by data (sometimes abbreviated UTD) is the idea that evidence available to us at a given time may be insufficient to determine what beliefs we should hold in response to it. The underdetermination thesis states that all evidence necessarily underdetermines any scientific theory. Underdetermination exists when available evidence is insufficient to identify which belief one should hold about that evidence. For example, if all that was known was that exactly $10 were spent on apples and oranges, and that apples cost $1 and oranges $2, then one would know enough to eliminate some possibilities (e.g., 6 oranges could not have been purchased), but one would not have enough evidence to know which specific combination of apples and oranges were purchased. In this example, one would say that belief in what combination was purchased is underdetermined by the available evidence. In contrast, ''overdetermin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ridge Regression
Ridge regression (also known as Tikhonov regularization, named for Andrey Tikhonov) is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in many fields including econometrics, chemistry, and engineering. It is a method of regularization of ill-posed problems. It is particularly useful to mitigate the problem of multicollinearity in linear regression, which commonly occurs in models with large numbers of parameters. In general, the method provides improved efficiency in parameter estimation problems in exchange for a tolerable amount of bias (see bias–variance tradeoff). The theory was first introduced by Hoerl and Kennard in 1970 in their ''Technometrics'' papers "Ridge regressions: biased estimation of nonorthogonal problems" and "Ridge regressions: applications in nonorthogonal problems". Ridge regression was developed as a possible solution to the imprecision of least ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lasso (statistics)
In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso, LASSO or L1 regularization) is a regression analysis method that performs both variable selection and Regularization (mathematics), regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. The lasso method assumes that the coefficients of the linear model are sparse, meaning that few of them are non-zero. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dropout (neural Networks)
Dropout and dilution (also called DropConnect) are regularization techniques for reducing overfitting in artificial neural networks by preventing complex co-adaptations on training data. They are an efficient way of performing model averaging with neural networks. ''Dilution'' refers to randomly decreasing weights towards zero, while ''dropout'' refers to randomly setting the outputs of hidden neurons to zero. Both are usually performed during the training process of a neural network, not during inference. Types and uses Dilution is usually split in ''weak dilution'' and ''strong dilution''. Weak dilution describes the process in which the finite fraction of removed connections is small, and strong dilution refers to when this fraction is large. There is no clear distinction on where the limit between strong and weak dilution is, and often the distinction is dependent on the precedent of a specific use-case and has implications for how to solve for exact solutions. Sometimes d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |