Coxeter notation

In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.

Reflectional groups

For Coxeter groups, defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter diagram. It uses the same simplification, suppressing 2s between orthogonal mirrors.

The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear diagram. So the ''A''_''n'' group is represented by ^''n''−1 to imply ''n'' nodes connected by ''n−1'' order-3 branches. Example ''A''₂ = ,3= ²or ^1,1represents diagrams or .

Coxeter initially represented bifurcating diagrams with vertical positioning of numbers, but later abbreviated with an exponent notation, like ..,3^p,qor ^p,q,r starting with ^1,1,1or ,3^1,1= or as D₄. Coxeter allowed for zeros as special cases to fit the ''A''_''n'' family, like ''A''₃ = ,3,3,3= ^4,0,0= ^4,0= ^3,1= ^2,2 like = = .

Coxeter groups formed by cyclic diagrams are represented by parentheseses inside of brackets, like p,q,r)= for the triangle group (p q r). If the branch orders are equal, they can be grouped as an exponent as the length the cycle in brackets, like 3,3,3,3)= ^[4/sup>">.html" ;"title="^{[4">[4/sup> representing Coxeter diagram or . can be represented as [3,(3,3,3)] or [3,3 /sup>].}

More complicated looping diagrams can also be expressed with care. The Coxeter–Dynkin diagram#Ranks 4.E2.80.9310, paracompact Coxeter group can be represented by Coxeter notation 3,3,(3),3,3) with nested/overlapping parentheses showing two adjacent 3,3,3)loops, and is also represented more compactly as ^[ �[ ">amp;nbsp;.html" ;"title=" ^{[ �[ /sup>">nbsp;">[ �[ ">amp;nbsp;.html" ;"title="[ ">[ �[ /sup> representing the rhombic symmetry of the Coxeter diagram. The paracompact complete graph diagram or , is represented as rhombus">rhombic symmetry of the Coxeter diagram. The paracompact complete graph diagram or , is represented as [3[3,3/sup>">[3,3">rhombus">rhombic symmetry of the Coxeter diagram. The paracompact complete graph diagram or , is represented as [3[3,3/sup>with the superscript ,3as the symmetry of its regular tetrahedron coxeter diagram.}

For the affine and hyperbolic groups, the subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's diagram.

Unconnected groups

The Coxeter diagram usually leaves order-2 branches undrawn, but the bracket notation includes an explicit 2 to connect the subgraphs. So the Coxeter diagram = ''A''₂×''A''₂ = 2''A''₂ can be represented by � = sup>2 = ,2,3 Sometimes explicit 2-branches may be included either with a 2 label, or with a line with a gap: or , as an identical presentation as ,2,3

Rank and dimension

Coxeter point group rank is equal to the number of nodes which is also equal to the dimension. A single mirror exists in 1-dimension, nbsp; , while in 2-dimensions or nbsp;� nbsp;sup>+. The 1 is a place-holder, not an actual branch order, but a marker for an orthogonal inactive mirror. The notation 'n'',1 represents a rank 3 group, as 'n''� nbsp;sup>+ or . Similarly, ,1as nbsp;� nbsp;sup>+× nbsp;sup>+ or order 2 and ,1sup>+ as nbsp;sup>+× nbsp;sup>+× nbsp;sup>+ or , order 1!

Subgroups

Coxeter's notation represents rotational/translational symmetry by adding a ⁺ superscript operator outside the brackets, sup>+ which cuts the order of the group in half, thus an index 2 subgroup. This operator implies an even number of operators must be applied, replacing reflections with rotations (or translations). When applied to a Coxeter group, this is called a direct subgroup because what remains are only direct isometries without reflective symmetry.

The ⁺ operators can also be applied inside of the brackets, like ,Y⁺or ,(Y,Z)⁺ and creates "semidirect" subgroups that may include both reflective and nonreflective generators. Semidirect subgroups can only apply to Coxeter group subgroups that have even order branches adjacent to it. Elements by parentheses inside of a Coxeter group can be give a ⁺ superscript operator, having the effect of dividing adjacent ordered branches into half order, thus is usually only applied with even numbers. For example, ,3⁺and ,(3,3)⁺().

If applied with adjacent odd branch, it doesn't create a subgroup of index 2, but instead creates overlapping fundamental domains, like ,1⁺= /2 which can define doubly wrapped polygons like a pentagram, , and ,3⁺relates to Schwarz triangle /2,3 density 2.

Groups without neighboring ⁺ elements can be seen in ringed nodes Coxeter-Dynkin diagram for uniform polytopes and honeycomb are related to ''hole'' nodes around the ⁺ elements, empty circles with the alternated nodes removed. So the snub cube, has symmetry ,3sup>+ (), and the snub tetrahedron, has symmetry ,3⁺(), and a demicube, h = ( or = ) has symmetry ⁺,4,3= ,3( or = = ).

Note: Pyritohedral symmetry can be written as , separating the graph with gaps for clarity, with the generators from the Coxeter group , producing pyritohedral generators , a reflection and 3-fold rotation. And chiral tetrahedral symmetry can be written as or , ⁺,4,3⁺= ,3sup>+, with generators .

Halving subgroups and extended groups

Johnson extends the ⁺ operator to work with a placeholder 1⁺ nodes, which removes mirrors, doubling the size of the fundamental domain and cuts the group order in half.Johnson (2018), 11.6 ''Subgroups and extensions'', p 255, halving subgroups In general this operation only applies to individual mirrors bounded by even-order branches. The 1 represents a mirror so pcan be seen as 1">p,1 1,2p">span style="color:red;">1,2p or 1,2p,1">span style="color:red;">1,2p,1 like diagram or , with 2 mirrors related by an order-2p dihedral angle. The effect of a mirror removal is to duplicate connecting nodes, which can be seen in the Coxeter diagrams: = , or in bracket notation: 1">⁺,2p, 1= 1,p,1">span style="color:#00ff00;">1,p,1=

Each of these mirrors can be removed so h p= ⁺,2p,1= ,2p,1⁺= a reflective subgroup index 2. This can be shown in a Coxeter diagram by adding a ⁺ symbol above the node: = = .

If both mirrors are removed, a quarter subgroup is generated, with the branch order becoming a gyration point of half the order:
:q p= ⁺,2p,1⁺= sup>+, a rotational subgroup of index 4. = = = = .

For example, (with p=2): ,1⁺= ⁺,4= = nbsp;� nbsp; order 4. ⁺,4,1⁺= sup>+, order 2.

The opposite to halving is doubling which adds a mirror, bisecting a fundamental domain, and doubling the group order.
: = p
Halving operations apply for higher rank groups, like tetrahedral symmetry is a half group of octahedral group: h ,3= ⁺,4,3= ,3 removing half the mirrors at the 4-branch. The effect of a mirror removal is to duplicate all connecting nodes, which can be seen in the Coxeter diagrams: = , h p,3= ⁺,2p,3= p,3,3)

If nodes are indexed, half subgroups can be labeled with new mirrors as composites. Like , generators has subgroup = , generators , where mirror 0 is removed, and replaced by a copy of mirror 1 reflected across mirror 0. Also given , generators , it has half group = , generators .

Doubling by adding a mirror also applies in reversing the halving operation: = ,3 or more generally = p,q

Radical subgroups

Johnson also added an asterisk or star * operator for "radical" subgroups, that acts similar to the ⁺ operator, but removes rotational symmetry. The index of the radical subgroup is the order of the removed element. For example, ,3*≅ ,2 The removed subgroup is order 6 so ,2is an index 6 subgroup of ,3

The radical subgroups represent the inverse operation to an extended symmetry operation. For example, ,3*≅ ,2 and in reverse ,2can be extended as [2,2 ≅ ,3 The subgroups can be expressed as a Coxeter diagram: or ≅ . The removed node (mirror) causes adjacent mirror virtual mirrors to become real mirrors.

If ,3has generators , ,3⁺ index 2, has generators ; ⁺,4,3≅ ,3 index 2 has generators ; while radical subgroup ,3*≅ ,2 index 6, has generators ; and finally ⁺,4,3* index 12 has generators .

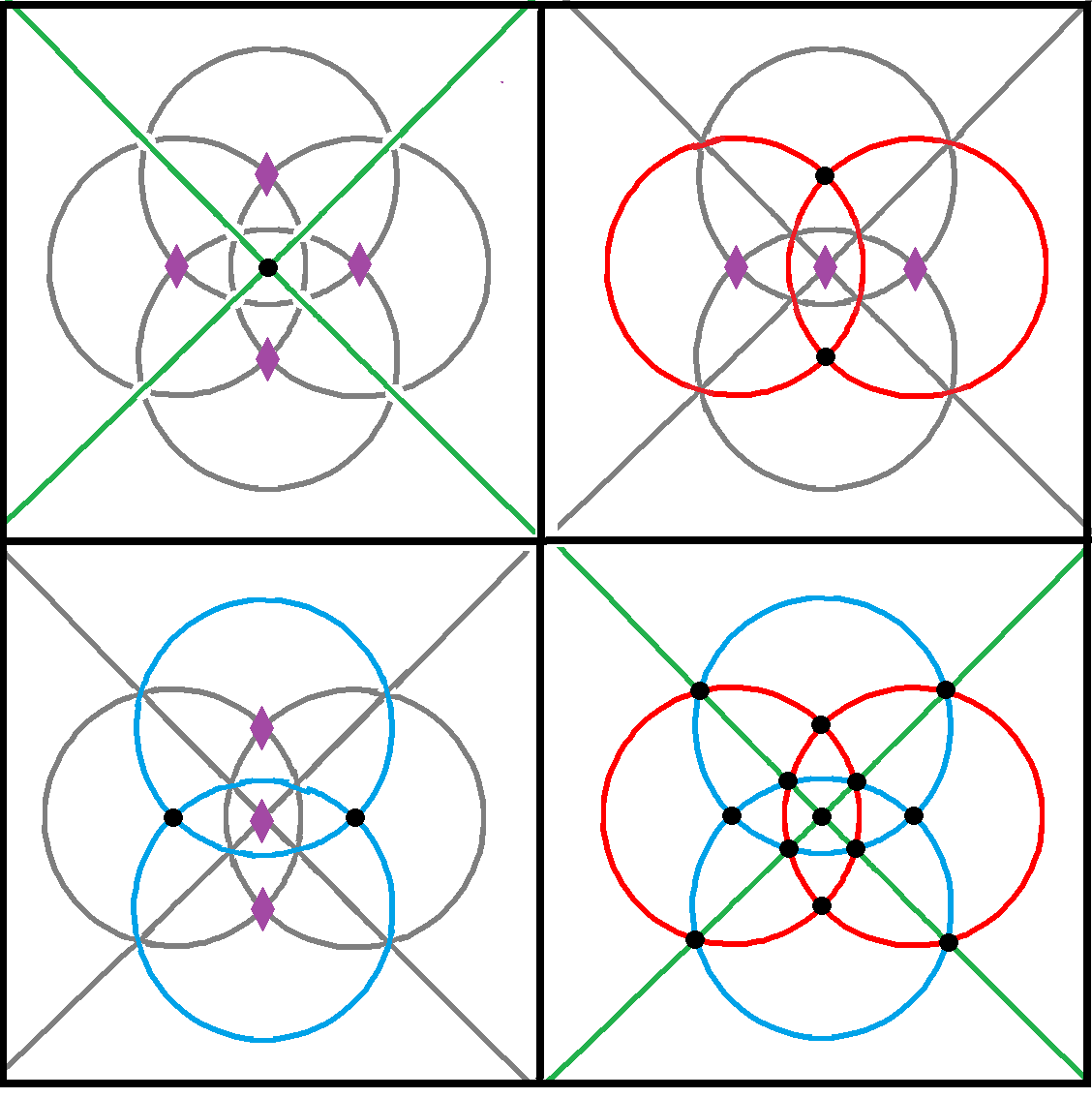
Trionic subgroups

A trionic subgroup is an index 3 subgroup. Johnson defines a ''trionic subgroup'' with operator ⅄, index 3. For rank 2 Coxeter groups, the trionic subgroup, ^⅄is a single mirror. And for ''p'' the trionic subgroup is ''p''sup>⅄ ≅ 'p'' Given , with generators , has 3 trionic subgroups. They can be differentiated by putting the ⅄ symbol next to the mirror generator to be removed, or on a branch for both: ''p'',1^⅄= = , = , and ''p''^⅄= = with generators , , or .

Trionic subgroups of tetrahedral symmetry: ,3sup>⅄ ≅ ⁺,4 relating the symmetry of the regular tetrahedron and tetragonal disphenoid.

For rank 3 Coxeter groups, 'p'',3 there is a trionic subgroup 'p'',3^⅄≅ 'p''/2,''p'' or = . For example, the finite group ,3^⅄≅ ,4 and Euclidean group ,3^⅄≅ ,6 and hyperbolic group ,3^⅄≅ ,8

An odd-order adjacent branch, ''p'', will not lower the group order, but create overlapping fundamental domains. The group order stays the same, while the density increases. For example, the icosahedral symmetry, ,3 of the regular polyhedra icosahedron becomes /2,5 the symmetry of 2 regular star polyhedra. It also relates the hyperbolic tilings , and star hyperbolic tilings

For rank 4, 'q'',2''p'',3^⅄= ''p'',((p,q,q)) = .

For example, ,4,3^⅄= ,3,3 or = , generators in ,4,3with the trionic subgroup ,3,3generators . For hyperbolic groups, ,6,3^⅄= /sup>">,3 ^{/sup> and ,4,3⅄= ,4,4}

Trionic subgroups of tetrahedral symmetry

]
Johnson identified two specific trionic subgroups of ,3 first an index 3 subgroup ,3sup>⅄ ≅ ⁺,4 with ,3( = = ) generators . It can also be written as 3,3,2^⅄)() as a reminder of its generators . This symmetry reduction is the relationship between the regular tetrahedron and the tetragonal disphenoid, represent a stretching of a tetrahedron perpendicular to two opposite edges.

Secondly he identifies a related index 6 subgroup ,3sup>Δ or 3,3,2^⅄)sup>+ (), index 3 from ,3sup>+ ≅ ,2sup>+, with generators , from ,3and its generators .

These subgroups also apply within larger Coxeter groups with ,3subgroup with neighboring branches all even order.
]
For example, 3,3)⁺,4 3,3)^⅄,4 and 3,3)^Δ,4are subgroups of ,3,4 index 2, 3 and 6 respectively. The generators of 3,3)^⅄,4≅ ≅ ,2⁺,8 order 128, are from ,3,4generators . And 3,3)^Δ,4≅ , order 64, has generators . As well, ^⅄,4,3^⅄≅ 3,3)^⅄,4

Also related ^1,1,1= ,3,4,1⁺has trionic subgroups: ^1,1,1sup>⅄ = 3,3)^⅄,4,1⁺ order 64, and 1= ^1,1,1sup>Δ = 3,3)^Δ,4,1⁺≅ 4,2⁺,4⁺, order 32.

Central inversion

A central inversion, order 2, is operationally differently by dimension. The group nbsp;sup>''n'' = ^''n''−1represents ''n'' orthogonal mirrors in n-dimensional space, or an n-flat subspace of a higher dimensional space. The mirrors of the group ^''n''−1are numbered . The order of the mirrors doesn't matter in the case of an inversion. The matrix of a central inversion is , the Identity matrix with negative one on the diagonal.

From that basis, the central inversion has a generator as the product of all the orthogonal mirrors. In Coxeter notation this inversion group is expressed by adding an alternation ⁺ to each 2 branch. The alternation symmetry is marked on Coxeter diagram nodes as open nodes.

A Coxeter-Dynkin diagram can be marked up with explicit 2 branches defining a linear sequence of mirrors, open-nodes, and shared double-open nodes to show the chaining of the reflection generators.

For example, ⁺,2and ,2⁺are subgroups index 2 of ,2 , and are represented as (or ) and (or ) with generators and respectively. Their common subgroup index 4 is ⁺,2⁺ and is represented by (or ), with the double-open marking a shared node in the two alternations, and a single rotoreflection generator .

Rotations and rotary reflections

Rotations and rotary reflections are constructed by a single single-generator product of all the reflections of a prismatic group, ''p''� ''q''�... where gcd(''p'',''q'',...)=1, they are isomorphic to the abstract cyclic group Z_n, of order ''n''=2''pq''.

The 4-dimensional double rotations, ''p''⁺,2⁺,2''q''⁺(with gcd(''p'',''q'')=1), which include a central group, and are expressed by Conway as ± _''p''×C_''q'' order 2''pq''. From Coxeter diagram , generators , requires two generator for ''p''⁺,2⁺,2''q''⁺ as . Half groups, ''p''⁺,2⁺,2''q''⁺sup>+, or cyclic graph, 2''p''⁺,2⁺,2''q''⁺,2⁺) expressed by Conway is _''p''×C_''q'' order ''pq'', with one generator, like .

If there is a common factor ''f'', the double rotation can be written as ''pf''⁺,2⁺,2''qf''⁺(with gcd(''p'',''q'')=1), generators , order 2''pqf''. For example, ''p''=''q''=1, ''f''=2, ⁺,2⁺,4⁺is order 4. And ''pf''⁺,2⁺,2''qf''⁺sup>+, generator , is order ''pqf''. For example, ⁺,2⁺,4⁺sup>+ is order 2, a central inversion.

In general a ''n''-rotation group, ''p''₁⁺,2,2''p''₂⁺,2,...,''p''_''n''⁺may require up to ''n'' generators if gcd(''p''₁,..,''p''_''n'')>1, as a product of all mirrors, and then swapping sequential pairs. The half group, ''p''₁⁺,2,2''p''₂⁺,2,...,''p''_''n''⁺sup>+ has generators squared. ''n''-rotary reflections are similar.

Commutator subgroups

Simple groups with only odd-order branch elements have only a single rotational/translational subgroup of order 2, which is also the commutator subgroup, examples ,3sup>+, ,5sup>+, ,3,3sup>+, ,3,5sup>+. For other Coxeter groups with even-order branches, the commutator subgroup has index 2^''c'', where c is the number of disconnected subgraphs when all the even-order branches are removed.

For example, ,4has three independent nodes in the Coxeter diagram when the 4s are removed, so its commutator subgroup is index 2³, and can have different representations, all with three ⁺ operators: ⁺,4⁺sup>+, ⁺,4,1⁺,4,1^{+ +},4,4,1⁺sup>+, or 4⁺,4⁺,2⁺) A general notation can be used with +''c'' as a group exponent, like ,4sup>+3.

Example subgroups

Rank 2 example subgroups

Dihedral symmetry groups with even-orders have a number of subgroups. This example shows two generator mirrors of in red and green, and looks at all subgroups by halfing, rank-reduction, and their direct subgroups. The group has two mirror generators 0, and 1. Each generate two virtual mirrors 101 and 010 by reflection across the other.

Rank 3 Euclidean example subgroups

The ,4group has 15 small index subgroups. This table shows them all, with a yellow fundamental domain for pure reflective groups, and alternating white and blue domains which are paired up to make rotational domains. Cyan, red, and green mirror lines correspond to the same colored nodes in the Coxeter diagram. Subgroup generators can be expressed as products of the original 3 mirrors of the fundamental domain, , corresponding to the 3 nodes of the Coxeter diagram, . A product of two intersecting reflection lines makes a rotation, like , , or . Removing a mirror causes two copies of neighboring mirrors, across the removed mirror, like , and . Two rotations in series cut the rotation order in half, like or , or . A product of all three mirrors creates a transreflection, like or .

Hyperbolic example subgroups

The same set of 15 small subgroups exists on all triangle groups with even order elements, like ,4in the hyperbolic plane:

Parabolic subgroups

A parabolic subgroup of a Coxeter group can be identified by removing one or more generator mirrors represented with a Coxeter diagram. For example the octahedral group has parabolic subgroups , , , , , . In bracket notation ,3has parabolic subgroups and a single mirror []. The order of the subgroup is known, and always an integer divisor group order, or index. Parabolic subgroups can also be written with x nodes, like = ,3subgroup by removing second mirror: or = = ,1^×,3=

Petrie subgroup

A ''petrie subgroup'' of an irreducible coxeter group can be created by the product of all of the generators. It can be seen in the skew regular petrie polygon of a regular polytope. The order of the new group is called the Coxeter number of the original Coxeter group. The ''Coxeter number'' of a Coxeter group is 2''m''/''n'', where ''n'' is the rank, and ''m'' is the number of reflections. A petrie subgroup can be written with a superscript. For example, ,3sup> is the petrie subgroup of a tetrahedral group, cyclic group order 4, generated by a rotoreflection. A rank 4 Coxeter group will have a double rotation generator, like ,3,3sup> is order 8.

Extended symmetry

Coxeter's notation includes double square bracket notation, to express automorphic symmetry within a Coxeter diagram. Johnson added alternative doubling by angled-bracket < . Johnson also added a prefix symmetry modifier [X, where Y can either represent symmetry of the Coxeter diagram of [X">[X.html" ;"title="[X">[X, where Y can either represent symmetry of the Coxeter diagram of [X or symmetry of the fundamental domain of [X].

For example, in 3D these equivalent rectangle and Rhombus, rhombic geometry diagrams of $_3$: and , the first doubled with square brackets, or twice doubled as [2 ^[4/sup>">.html" ;"title="^{[4">[4/sup>, with order 4 higher symmetry. To differentiate the second, angled brackets are used for doubling, < [4/sup>]> and twice doubled as <2 [4/sup>]>, also with a different order 4 symmetry. Finally a full symmetry where all 4 nodes are equivalent can be represented by [4/sup>">.html" ;"title="[4">[4/sup>, with the order 8, symmetry of the Square (geometry)">square. But by considering the tetragonal disphenoid fundamental domain the extended symmetry of the square graph can be marked more explicitly as [(2+,4) [4/sup>">.html" ;"title="[4">[4/sup> or [2+,4 [4/sup>">.html" ;"title="[4">[4/sup>.}

Further symmetry exists in the cyclic $_n$ and branching $D_3$, $_6$, and $_4$ diagrams. $_n$ has order 2''n'' symmetry of a regular ''n''-gon, , and is represented by [''n''[3^[''n'']. $D_3$ and $_6$ are represented by [3[3^1,1,1 = ,4,3and [3[3^2,2,2 respectively while $_4$ by 3,3)[3^1,1,1,1 = [3,3,4,3"><sup>1,1,1,1<_sup>.html" ;"title="3,3)[3^1,1,1,1">3,3)[3^1,1,1,1 = [3,3,4,3 with the diagram containing the order 24 symmetry of the regular tetrahedron, . The paracompact hyperbolic group $_5$ = [3^1,1,1,1,1], , contains the symmetry of a 5-cell, , and thus is represented by [(3,3,3)[3^1,1,1,1,1 = [3,4,3,3,3].

An asterisk * superscript is effectively an inverse operation, creating ''radical subgroups'' removing connected of odd-ordered mirrors.

Examples:

Looking at generators, the double symmetry is seen as adding a new operator that maps symmetric positions in the Coxeter diagram, making some original generators redundant. For 3D space groups, and 4D point groups, Coxeter defines an index two subgroup of , , which he defines as the product of the original generators of by the doubling generator. This looks similar to ⁺, which is the chiral subgroup of . So for example the 3D space groups ⁺ (I432, 211) and (Pmn,
223) are distinct subgroups of (Imm, 229).

Rank one groups

In one dimension, the ''bilateral group'' nbsp;represents a single mirror symmetry, abstract ''Dih''₁ or ''Z''₂, symmetry order 2. It is represented as a Coxeter–Dynkin diagram with a single node, . The '' identity group'' is the direct subgroup nbsp;sup>+, Z₁, symmetry order 1. The + superscript simply implies that alternate mirror reflections are ignored, leaving the identity group in this simplest case. Coxeter used a single open node to represent an alternation, .

Rank two groups

In two dimensions, the ''rectangular group'' abstract D₂² or D₄, also can be represented as a direct product � being the product of two bilateral groups, represents two orthogonal mirrors, with Coxeter diagram, , with order 4. The 2 in comes from linearization of the orthogonal subgraphs in the Coxeter diagram, as with explicit branch order 2. The ''rhombic group'', sup>+ ( or ), half of the rectangular group, the point reflection symmetry, Z₂, order 2.

Coxeter notation to allow a 1 place-holder for lower rank groups, so is the same as and ⁺or sup>+ is the same as sup>+ and Coxeter diagram .

The ''full p-gonal group'' abstract ''dihedral group'' D_2''p'', ( nonabelian for p>2), of order 2''p'', is generated by two mirrors at angle ''π''/''p'', represented by Coxeter diagram . The ''p-gonal'' subgroup sup>+, ''cyclic group'' ''Z''_''p'', of order ''p'', generated by a rotation angle of ''π''/''p''.

Coxeter notation uses double-bracking to represent an automorphic ''doubling'' of symmetry by adding a bisecting mirror to the fundamental domain. For example, p adds a bisecting mirror to and is isomorphic to p

In the limit, going down to one dimensions, the ''full apeirogonal group'' is obtained when the angle goes to zero, so �� abstractly the infinite dihedral group D_∞, represents two parallel mirrors and has a Coxeter diagram . The '' apeirogonal group'' ��sup>+, , abstractly the infinite cyclic group Z_∞, isomorphic to the ''additive group'' of the integers, is generated by a single nonzero translation.

In the hyperbolic plane, there is a ''full pseudogonal group'' 'iπ/λ'' and ''pseudogonal subgroup'' 'iπ/λ''sup>+, . These groups exist in regular infinite-sided polygons, with edge length λ. The mirrors are all orthogonal to a single line.

Rank three groups

Point groups in 3 dimensions can be expressed in bracket notation related to the rank 3 Coxeter groups:

In three dimensions, the ''full orthorhombic group'' or ''orthorectangular'' ,2 abstractly Z₂³, order 8, represents three orthogonal mirrors, (also represented by Coxeter diagram as three separate dots ). It can also can be represented as a direct product � � but the ,2expression allows subgroups to be defined:

First there is a "semidirect" subgroup, the ''orthorhombic group'', ,2⁺( or ), abstractly Z₂×''Z''₂, of order 4. When the + superscript is given inside of the brackets, it means reflections generated only from the adjacent mirrors (as defined by the Coxeter diagram, ) are alternated. In general, the branch orders neighboring the + node must be even. In this case ,2⁺and ⁺,2represent two isomorphic subgroups that are geometrically distinct. The other subgroups are the ''pararhombic group'' ,2sup>+ ( or ), also order 4, and finally the '' central group'' ⁺,2⁺( or ) of order 2.

Next there is the ''full ortho-''p''-gonal group'', ,p(), abstractly Z₂×D_2''p'', of order 4p, representing two mirrors at a dihedral angle π/''p'', and both are orthogonal to a third mirror. It is also represented by Coxeter diagram as .

The direct subgroup is called the para-''p''-gonal group, ,psup>+ ( or ), abstractly D_2''p'', of order 2p, and another subgroup is ,p⁺() abstractly Z₂×''Z''_''p'', also of order 2p.

The ''full gyro-p-gonal group'', ⁺,2''p''( or ), abstractly D_4''p'', of order 4''p''. The gyro-''p''-gonal group, ⁺,2p⁺( or ), abstractly ''Z''_2''p'', of order 2''p'' is a subgroup of both ⁺,2''p''and ,2''p''⁺

The polyhedral groups are based on the symmetry of platonic solids: the tetrahedron, octahedron, cube, icosahedron, and dodecahedron, with Schläfli symbols , , , , and respectively. The Coxeter groups for these are: ,3(), ,4(), ,5() called full tetrahedral symmetry, octahedral symmetry, and icosahedral symmetry, with orders of 24, 48, and 120.

In all these symmetries, alternate reflections can be removed producing the rotational tetrahedral ,3sup>+(), octahedral ,4sup>+ (), and icosahedral ,5sup>+ () groups of order 12, 24, and 60. The octahedral group also has a unique index 2 subgroup called the pyritohedral symmetry group, ⁺,4( or ), of order 12, with a mixture of rotational and reflectional symmetry. Pyritohedral symmetry is also an index 5 subgroup of icosahedral symmetry: --> , with virtual mirror 1 across 0, , and 3-fold rotation .

The tetrahedral group, ,3(), has a doubling (which can be represented by colored nodes ), mapping the first and last mirrors onto each other, and this produces the ,4( or ) group. The subgroup ,4,1⁺( or ) is the same as ,3 and ⁺,4,1⁺( or ) is the same as ,3sup>+.

Affine

In the Euclidean plane there's 3 fundamental reflective groups generated by 3 mirrors, represented by Coxeter diagrams , , and , and are given Coxeter notation as ,4 ,3 and 3,3,3) The parentheses of the last group imply the diagram cycle, and also has a shorthand notation /sup>"> ^/sup>

as a doubling of the ,4group produced the same symmetry rotated π/4 from the original set of mirrors.

Direct subgroups of rotational symmetry are: ,4sup>+, ,3sup>+, and 3,3,3)sup>+. ⁺,4and ,3⁺are semidirect subgroups.

Given in Coxeter notation (orbifold notation), some low index affine subgroups are:

Rank four groups

Point groups

Rank four groups defined the 4-dimensional point groups:

Subgroups

Space groups

Line groups

Rank four groups also defined the 3-dimensional line groups:

Duoprismatic group

Rank four groups defined the 4-dimensional duoprismatic groups. In the limit as p and q go to infinity, they degenerate into 2 dimensions and the wallpaper groups.

Wallpaper groups

Rank four groups also defined some of the 2-dimensional wallpaper groups, as limiting cases of the four-dimensional duoprism groups:

Subgroups of ��,2,∞ (*2222) can be expressed down to its index 16 commutator subgroup:

Complex reflections

Coxeter notation has been extended to Complex space, Cⁿ where nodes are unitary reflections of period 2 or greater. Nodes are labeled by an index, assumed to be 2 for ordinary real reflection if suppressed. Complex reflection groups are called Shephard groups rather than Coxeter groups, and can be used to construct complex polytopes.

In $\mathbb^1$, a rank 1 Shephard group , order ''p'', is represented as _''p'' sub>''p'' or ]_''p'' It has a single generator, representing a 2''π''/''p'' radian rotation in the Complex plane: $e^$.

Coxeter writes the rank 2 complex group, _''p'' 'q''sub>''r'' represents Coxeter diagram . The ''p'' and ''r'' should only be suppressed if both are 2, which is the real case [''q'']. The order of a rank 2 group _''p'' 'q''sub>''r'' is $g = 8/q(1/p+2/q+1/r-1)^$.Coxeter, Regular Complex Polytopes, 9.7 Two-generator subgroups reflections. pp. 178–179

The rank 2 solutions that generate complex polygons are: _''p'' sub>2 (''p'' is 2,3,4,...), ₃ sub>3, ₃ sub>2, ₃ sub>3, ₄ sub>4, ₃ sub>2, ₄ sub>2, ₄ sub>3, ₃ sub>3, ₅ sub>5, ₃ 0sub>2, ₅ sub>2, and ₅ sub>3 with Coxeter diagrams , , , , , , , , , , , , .

Infinite groups are ₃ 2sub>2, ₄ sub>2, ₆ sub>2, ₃ sub>3, ₆ sub>3, ₄ sub>4, and ₆ sub>6 or , , , , , , .

Index 2 subgroups exists by removing a real reflection: _''p'' ''q''sub>2 → _''p'' 'q''sub>''p''. Also index ''r'' subgroups exist for 4 branches: _''p'' sub>''r'' → _''p'' 'r''sub>''p''.

For the infinite family _''p'' sub>2, for any ''p'' = 2, 3, 4,..., there are two subgroups: _''p'' sub>2 → 'p'' index ''p'', while and _''p'' sub>2 → _''p'' �_''p'' index 2.

Computation with reflection matrices as symmetry generators

A Coxeter group, represented by Coxeter diagram , is given Coxeter notation ,qfor the branch orders. Each node in the Coxeter diagram represents a mirror, by convention called ρ_i (and matrix R_i). The ''generators'' of this group ,qare reflections: ρ₀, ρ₁, and ρ₂. Rotational subsymmetry is given as products of reflections: By convention, σ_0,1 (and matrix S_0,1) = ρ₀ρ₁ represents a rotation of angle π/p, and σ_1,2 = ρ₁ρ₂ is a rotation of angle π/q, and σ_0,2 = ρ₀ρ₂ represents a rotation of angle π/2.

,qsup>+, , is an index 2 subgroup represented by two rotation generators, each a products of two reflections: σ_0,1, σ_1,2, and representing rotations of π/''p'', and π/''q'' angles respectively.

With one even branch, 'p''⁺,2''q'' or , is another subgroup of index 2, represented by rotation generator σ_0,1, and reflectional ρ₂.

With even branches, ''p''⁺,2''q''⁺ , is a subgroup of index 4 with two generators, constructed as a product of all three reflection matrices: By convention as: ψ_0,1,2 and ψ_1,2,0, which are rotary reflections, representing a reflection and rotation or reflection.

In the case of affine Coxeter groups like , or , one mirror, usually the last, is translated off the origin. A translation generator τ_0,1 (and matrix T_0,1) is constructed as the product of two (or an even number of) reflections, including the affine reflection. A transreflection (reflection plus a translation) can be the product of an odd number of reflections φ_0,1,2 (and matrix V_0,1,2), like the index 4 subgroup : ⁺,4⁺= .

Another composite generator, by convention as ζ (and matrix Z), represents the inversion, mapping a point to its inverse. For ,3and ,3 ζ = (ρ₀ρ₁ρ₂)^h/2, where ''h'' is 6 and 10 respectively, the Coxeter number for each family. For 3D Coxeter group ,q(), this subgroup is a rotary reflection ⁺,h⁺

Coxeter groups are categorized by their rank, being the number of nodes in its Coxeter-Dynkin diagram. The structure of the groups are also given with their abstract group types: In this article, the abstract dihedral groups are represented as ''Dih''_n, and cyclic groups are represented by ''Z''_n, with ''Dih''₁=''Z''₂.

Rank 2

Example, in 2D, the Coxeter group 'p''() is represented by two reflection matrices R₀ and R₁, The cyclic symmetry 'p''sup>+ () is represented by rotation generator of matrix S_0,1.

Rank 3

The finite rank 3 Coxeter groups are ,''p'' ,''p'' ,3 ,4 and ,5

To reflect a point through a plane $ax + by + cz = 0$ (which goes through the origin), one can use $\mathbf = \mathbf - 2\mathbf^T$, where $\mathbf$ is the 3×3 identity matrix and $\mathbf$ is the three-dimensional unit vector for the vector normal of the plane. If the L2 norm of $a, b,$ and $c$ is unity, the transformation matrix can be expressed as:

:\mathbf = \left begin 1 - 2 a^2 & - 2 a b & - 2 a c \\ - 2 a b & 1 - 2 b^2 & - 2 b c \\ - 2 a c & - 2 b c & 1 - 2c^2 \end\right /math>

'p'',2

The reducible 3-dimensional finite reflective group is dihedral symmetry, 'p'',2 order 4''p'', . The reflection generators are matrices R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)³=(R₁×R₂)³=(R₀×R₂)²=Identity. 'p'',2sup>+ () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. An order ''p'' rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

,3

The simplest irreducible 3-dimensional finite reflective group is tetrahedral symmetry, ,3 order 24, . The reflection generators, from a D₃=A₃ construction, are matrices R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)³=(R₁×R₂)³=(R₀×R₂)²=Identity. ,3sup>+ () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. A trionic subgroup, isomorphic to ⁺,4 order 8, is generated by S_0,2 and R₁. An order 4 rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

,3

Another irreducible 3-dimensional finite reflective group is octahedral symmetry, ,3 order 48, . The reflection generators matrices are R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)⁴=(R₁×R₂)³=(R₀×R₂)²=Identity. Chiral octahedral symmetry, ,3sup>+, () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. Pyritohedral symmetry ,3⁺ () is generated by reflection R₀ and rotation S_1,2. A 6-fold rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

,3

A final irreducible 3-dimensional finite reflective group is icosahedral symmetry, ,3 order 120, . The reflection generators matrices are R₀, R₁, R₂. R₀²=R₁²=R₂²=(R₀×R₁)⁵=(R₁×R₂)³=(R₀×R₂)²=Identity. ,3sup>+ () is generated by 2 of 3 rotations: S_0,1, S_1,2, and S_0,2. A 10-fold rotoreflection is generated by V_0,1,2, the product of all 3 reflections.

Rank 4

There are 4 irreducible Coxeter groups in 4 dimensions: ,3,3 ,3,3 ^1,1,1 ,4,4 ,3,3 as well as an infinite family of duoprismatic groups 'p'',2,''q''

'p'',2,''q''

The duprismatic group, 'p'',2,''q'' has order 4''pq''.

= ''p'',2,''p''

=
The duoprismatic group can double in order, to 8''p''², with a 2-fold rotation between the two planes.

,3,3

Hypertetrahedral symmetry, ,3,3 order 120, is easiest to represent with 4 mirrors in 5-dimensions, as a subgroup of ,3,3,3

= 3,3,3

=
The extended group 3,3,3, order 240, is doubled by a 2-fold rotation matrix T, here reversing coordinate order and sign: There are 3 generators . Since T is self-reciprocal R₃=TR₀T, and R₂=TR₁T.

,3,3

A irreducible 4-dimensional finite reflective group is hyperoctahedral group (or hexadecachoric group (for 16-cell), B₄= ,3,3 order 384, . The reflection generators matrices are R₀, R₁, R₂, R₃. R₀²=R₁²=R₂²=R₃²=(R₀×R₁)⁴=(R₁×R₂)³=(R₂×R₃)³=(R₀×R₂)²=(R₁×R₃)²=(R₀×R₃)²=Identity.

Chiral hyperoctahedral symmetry, ,3,3sup>+, () is generated by 3 of 6 rotations: S_0,1, S_1,2, S_2,3, S_0,2, S_1,3, and S_0,3. Hyperpyritohedral symmetry ,(3,3)⁺ () is generated by reflection R₀ and rotations S_1,2 and S_2,3. An 8-fold double rotation is generated by W_0,1,2,3, the product of all 4 reflections.

= ,3^1,1

=
A half group of ,3,3is ,3^1,1 , order 192. It shares 3 generators with ,3,3group, but has two copies of an adjacent generator, one reflected across the removed mirror.

,4,3

A irreducible 4-dimensional finite reflective group is Icositetrachoric group (for 24-cell), F₄= ,4,3 order 1152, . The reflection generators matrices are R₀, R₁, R₂, R₃. R₀²=R₁²=R₂²=R₃²=(R₀×R₁)³=(R₁×R₂)⁴=(R₂×R₃)³=(R₀×R₂)²=(R₁×R₃)²=(R₀×R₃)²=Identity.

Chiral icositetrachoric symmetry, ,4,3sup>+, () is generated by 3 of 6 rotations: S_0,1, S_1,2, S_2,3, S_0,2, S_1,3, and S_0,3. Ionic diminished ,4,3⁺group, () is generated by reflection R₀ and rotations S_1,2 and S_2,3. A 12-fold double rotation is generated by W_0,1,2,3, the product of all 4 reflections.

= 3,4,3

=

The group 3,4,3 extends ,4,3by a 2-fold rotation, T, doubling order to 2304.

,3,3

The hyper-icosahedral symmetry, ,3,3 order 14400, . The reflection generators matrices are R₀, R₁, R₂, R₃. R₀²=R₁²=R₂²=R₃²=(R₀×R₁)⁵=(R₁×R₂)³=(R₂×R₃)³=(R₀×R₂)²=(R₀×R₃)²=(R₁×R₃)²=Identity. ,3,3sup>+ () is generated by 3 rotations: S_0,1 = R₀×R₁, S_1,2 = R₁×R₂, S_2,3 = R₂×R₃, etc.

Rank 8

^4,2,1

The E8 Coxeter group, ^4,2,1 , has 8 mirror nodes, order 696729600 (192x10!). E7 and E6, ^3,2,1 , and ^2,2,1 can be constructed by ignoring the first mirror or the first two mirrors respectively.

Affine rank 2

Affine matrices are represented by adding an extra row and column, the last row being zero except last entry 1. The last column represents a translation vector.

��

The affine group �� , can be given by two reflection matrices, x=0 and x=1.

Affine rank 3

,4

The affine group ,4 , (p4m), can be given by three reflection matrices, reflections across the x axis (y=0), a diagonal (x=y), and the affine reflection across the line (x=1). ,4sup>+ () (p4) is generated by S_0,1 S_1,2, and S_0,2. ⁺,4⁺() (pgg) is generated by 2-fold rotation S_0,2 and glide reflection (transreflection) V_0,1,2. ⁺,4() (p4g) is generated by S_0,1 and R₃. The group 4,4,2⁺)() (cmm), is generated by 2-fold rotation S_1,3 and reflection R₂.

,6/h3>

The affine group ,6 , (p6m), can be given by three reflection matrices, reflections across the x axis (y=0), line y=(√3/2)x, and vertical line x=1.

/sup>"> ^/sup>

The affine group /sup>"> /sup>can be constructed as a half group of . R₂ is replaced by R'₂ = R₂×R₁×R₂, presented by the hyperplane: y+(√3/2)x=2. The fundamental domain is an equilateral triangle with edge length 2.

Affine rank 4

,3,4

The affine group is ,3,4(), can be given by four reflection matrices. Mirror R₀ can be put on z=0 plane. Mirror R₁ can be put on plane y=z. Mirror R₂ can be put on x=y plane. Mirror R₃ can be put on x=1 plane. ,3,4sup>+ () is generated by S_0,1, S_1,2, and S_2,3.

= 4,3,4

=
The extended group 4,3,4 doubles the group order, adding with a 2-fold rotation matrix T, with a fixed axis through points (1,1/2,0) and (1/2,1/2,1/2). The generators are . R₂ = T×R₁×T and R₃ = T×R₀×T.

,3^1,1

The group ,3^1,1can be constructed from ,3,4 by computing ,3,4,1⁺ , as R'₃=R₃×R₂×R₃, with new R'₃ as an image of R₂ across R₃.

^[4/sup>">.html" ;"title="^[4">[4/sup>

The group ^[4/sup>">.html" ;"title="[4">[4/sup>can be constructed from ,3,4 by removing first and last mirrors, [1⁺,4,3,4,1⁺], , by R'₁=R₀×R₁×R₀ and R'₃=R₃×R₂×R₃.

Notes

References

* Harold Scott MacDonald Coxeter, H.S.M. Coxeter:
** Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,

*** (Paper 22)
*** (Paper 23)
*** (Paper 24)
*
* Norman Johnson ''Uniform Polytopes'', Manuscript (1991)
** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. (1966)
** Norman W. Johnson and Asia Ivic Weis
Quadratic Integers and Coxeter Groups
PDF Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336
** N. W. Johnson: ''Geometries and Transformations'', (2018)
PDF
*
* John H. Conway and Derek A. Smith, ''On Quaternions and Octonions'', 2003,
* ''The Symmetries of Things'' 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, {{ISBN, 978-1-56881-220-5 Ch.22 ''35 prime space groups'', ch.25 ''184 composite space groups'', ch.26 ''Higher still'', 4D point groups

Symmetry
Group theory