|
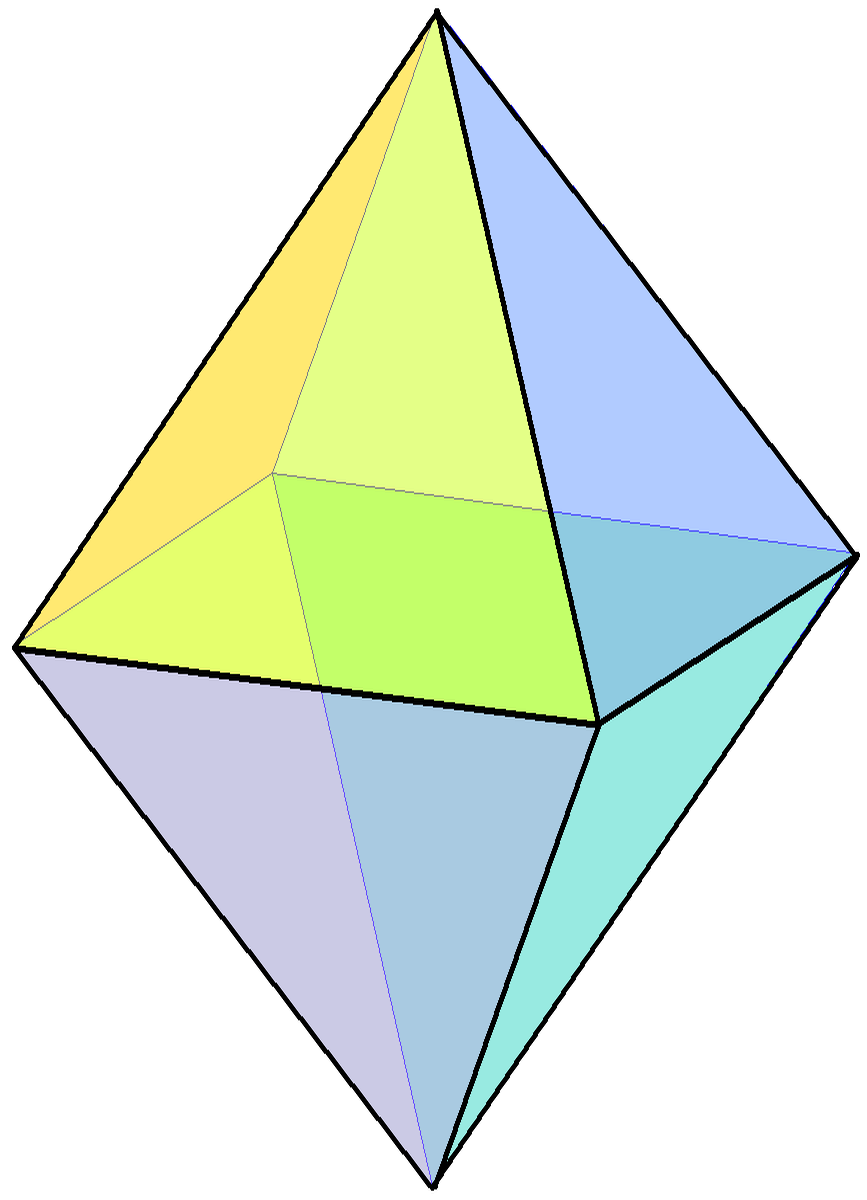
Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Regular Octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyhedron; many types of irregular octahedra also exist. A regular octahedron is convex, meaning that for any two points within it, the line segment connecting them lies entirely within it. It is one of the eight convex deltahedra because all of the faces are equilateral triangles. It is a composite polyhedron made by attaching two equilateral square pyramids. Its dual polyhedron is the cube, and they have the same three-dimensional symmetry groups, the octahedral symmetry \mathrm_\mathrm . A regular octahedron is a special case of an octahedron, any eight-sided polyhedron. It is the three-dimensional case of the more general concept of a cross-polytope. As a Platonic solid The regular octahedron is one of the Platonic solids, a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Uniform Polyhedron
In geometry, a uniform polyhedron has regular polygons as Face (geometry), faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruence (geometry), congruent. Uniform polyhedra may be Regular polyhedron, regular (if also Isohedral figure, face- and Isotoxal figure, edge-transitive), Quasiregular polyhedron, quasi-regular (if also edge-transitive but not face-transitive), or Semiregular polyhedron, semi-regular (if neither edge- nor face-transitive). The faces and vertices don't need to be Convex polyhedron, convex, so many of the uniform polyhedra are also Star polyhedron, star polyhedra. There are two infinite classes of uniform polyhedra, together with 75 other polyhedra. They are 2 infinite classes of Prism (geometry), prisms and antiprisms, the convex polyhedrons as in 5 Platonic solids and 13 Archimedean solids—2 Quasiregular polyhedron, quasiregular and 11 Semiregular polyhedron, semiregular&m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Platonic Solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (identical in shape and size) regular polygons (all angles congruent and all edge (geometry), edges congruent), and the same number of faces meet at each Vertex (geometry), vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato, who hypothesized in one of his dialogues, the ''Timaeus (dialogue), Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex set, convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all thr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
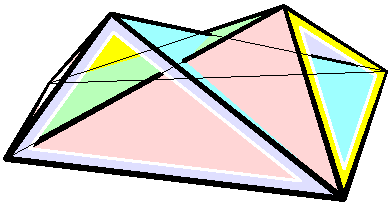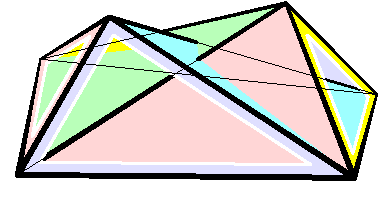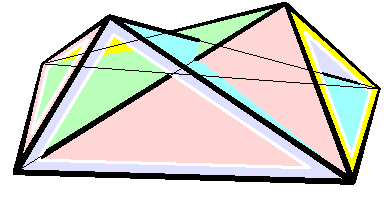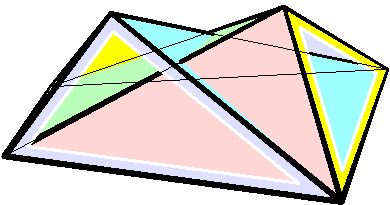
Bricard Octahedron
In geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ..., a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. These octahedra were the first flexible polyhedra to be discovered.. The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, but there exist other flexible polyhedra without self-crossings. Avoiding self-crossing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Truncated Tetrahedron
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncation (geometry), truncating all 4 vertices of a regular tetrahedron. Construction The truncated tetrahedron can be constructed from a regular tetrahedron by cutting all of its vertices off, a process known as Truncation (geometry), truncation. The resulting polyhedron has 4 equilateral triangles and 4 regular hexagons, 18 edges, and 12 vertices. With edge length 1, the Cartesian coordinates of the 12 vertices are points \bigl( , \pm\tfrac, \pm\tfrac \bigr) that have an even number of minus signs. Properties Given the edge length a . The surface area of a truncated tetrahedron A is the sum of 4 regular hexagons and 4 equilateral triangles' area, and its volume V is: \begin A &= 7\sqrta^2 &&\approx 12.124a^2, \\ V &= \tfrac\sqrta^3 &&\approx 2.711a^3. \end The dihedral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bipyramid
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two Pyramid (geometry), pyramids together base (geometry), base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base Vertex (geometry), vertices are usually coplanar and a bipyramid is usually ''symmetric'', meaning the two pyramids are mirror images across their common base plane. When each apex (geometry), apex (, the off-base vertices) of the bipyramid is on a line perpendicular to the base and passing through its center, it is a ''right'' bipyramid; otherwise it is ''oblique''. When the base is a regular polygon, the bipyramid is also called ''regular''. Definition and properties A bipyramid is a polyhedron constructed by fusing two Pyramid (geometry), pyramids which share the same polygonal base (geometry), base; a pyramid is in turn constructed by connecting each vertex of its base to a single new vertex (geometry), vertex (th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Equilateral Triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties. The equilateral triangle can be found in various tilings, and in polyhedrons such as the deltahedron and antiprism. It appears in real life in popular culture, architecture, and the study of stereochemistry resembling the molecular known as the trigonal planar molecular geometry. Properties An equilateral triangle is a triangle that has three equal sides. It is a special case of an isosceles triangle in the modern definition, stating that an isosceles triangle is defined at least as having two equal sides. Based on the modern definition, this leads to an equilateral triangle in which one of the three sides may be considered its base. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombus, rhombi, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Augmented Triangular Prism
In geometry, the augmented triangular prism is a polyhedron constructed by attaching an equilateral square pyramid onto the square face of a triangular prism. As a result, it is an example of Johnson solid. It can be visualized as the chemical compound, known as capped trigonal prismatic molecular geometry. Construction The augmented triangular prism can be constructed from a triangular prism by attaching an equilateral square pyramid to one of its square faces, a process known as augmentation. This square pyramid covers the square face of the prism, so the resulting polyhedron has 6 equilateral triangles and 2 squares as its faces. A convex polyhedron in which all faces are regular is Johnson solid, and the augmented triangular prism is among them, enumerated as 49th Johnson solid J_ . Properties An augmented triangular prism with edge length a has a surface area, calculated by adding six equilateral triangles and two squares' area: \fraca^2 \approx 4.598a^2. Its v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tetragonal Trapezohedron
In geometry, a tetragonal trapezohedron, or deltohedron, is the second in an infinite series of trapezohedra, which are dual to the antiprisms. It has eight faces, which are congruent kites, and is dual to the square antiprism. Applications In mesh generation This shape has been used as a test case for hexahedral mesh generation,..... simplifying an earlier test case posited by mathematician Robert Schneiders in the form of a square pyramid with its boundary subdivided into 16 quadrilaterals. In this context the tetragonal trapezohedron has also been called the cubical octahedron, quadrilateral octahedron, or octagonal spindle, because it has eight quadrilateral faces and is uniquely defined as a combinatorial polyhedron by that property. Adding four cuboids to a mesh for the cubical octahedron would also give a mesh for Schneiders' pyramid. As a simply-connected polyhedron with an even number of quadrilateral faces, the cubical octahedron can be decomposed into topologica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |