regular octahedron on:
[Wikipedia]
[Google]
[Amazon]
In
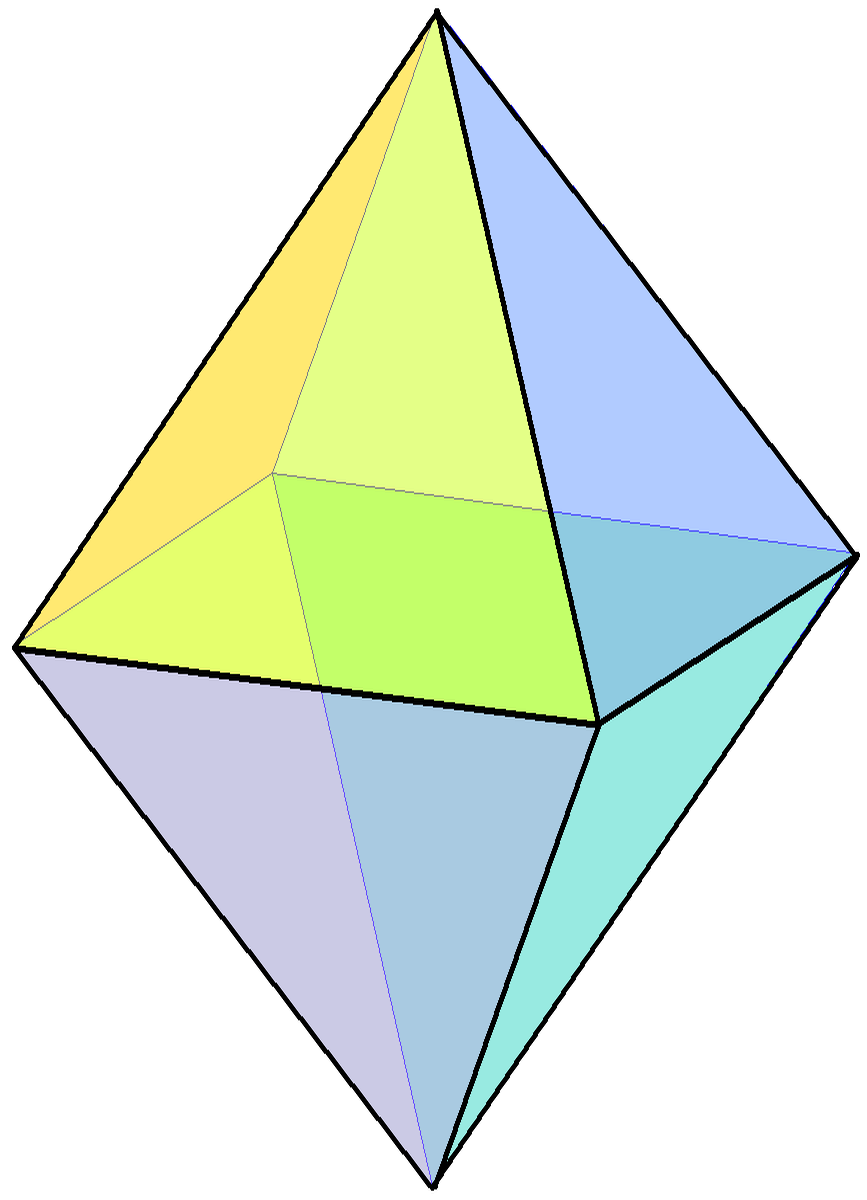 Many octahedra of interest are square bipyramids. A square bipyramid is a
Many octahedra of interest are square bipyramids. A square bipyramid is a
 The surface area of a regular octahedron can be ascertained by summing all of its eight equilateral triangles, whereas its volume is twice the volume of a square pyramid; if the edge length is ,
The radius of a
The surface area of a regular octahedron can be ascertained by summing all of its eight equilateral triangles, whereas its volume is twice the volume of a square pyramid; if the edge length is ,
The radius of a
 The
The
 The interior of the compound of two dual tetrahedra is an octahedron, and this compound—called the stella octangula—is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and
The interior of the compound of two dual tetrahedra is an octahedron, and this compound—called the stella octangula—is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and
Editable printable net of an octahedron with interactive 3D view
Paper model of the octahedron
* ttp://www.mathconsult.ch/showroom/unipoly/ The Uniform Polyhedra
Virtual Reality Polyhedra
– The Encyclopedia of Polyhedra *
– Try: dP4 {{Authority control Deltahedra Individual graphs Platonic solids Prismatoid polyhedra Bipyramids
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a regular octahedron is a Platonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
composed of eight equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
s, four of which meet at each vertex. Regular octahedra occur in nature as crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
structures. An octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
, more generally, can be any eight-sided polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer ...
; many types of irregular octahedra also exist.
A regular octahedron is convex, meaning that for any two points within it, the line segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special c ...
connecting them lies entirely within it. It is one of the eight convex deltahedra
A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron was named by Martyn Cundy, after the Greek capital letter Delta (letter), delta resembling a triangular shape Δ.
Deltahedra can be categorized by the prope ...
because all of the faces are equilateral triangles. It is a composite polyhedron made by attaching two equilateral square pyramids. Its dual polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other ...
is the cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
, and they have the same three-dimensional symmetry groups, the octahedral symmetry .
A regular octahedron is a special case of an octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
, any eight-sided polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer ...
. It is the three-dimensional case of the more general concept of a cross-polytope.
As a Platonic solid
The regular octahedron is one of thePlatonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
s, a set of polyhedrons whose faces are congruent regular polygons and the same number of faces meet at each vertex. This ancient set of polyhedrons was named after Plato
Plato ( ; Greek language, Greek: , ; born BC, died 348/347 BC) was an ancient Greek philosopher of the Classical Greece, Classical period who is considered a foundational thinker in Western philosophy and an innovator of the writte ...
who, in his ''Timaeus'' dialogue, related these solids to nature. One of them, the regular octahedron, represented the classical element
The classical elements typically refer to Earth (classical element), earth, Water (classical element), water, Air (classical element), air, Fire (classical element), fire, and (later) Aether (classical element), aether which were proposed to ...
of wind
Wind is the natural movement of atmosphere of Earth, air or other gases relative to a planetary surface, planet's surface. Winds occur on a range of scales, from thunderstorm flows lasting tens of minutes, to local breezes generated by heatin ...
.
Following its attribution with nature by Plato, Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
in his '' Harmonices Mundi'' sketched each of the Platonic solids. In his '' Mysterium Cosmographicum'', Kepler also proposed the Solar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Sola ...
by using the Platonic solids setting into another one and separating them with six spheres resembling the six planets. The ordered solids started from the innermost to the outermost: regular octahedron, regular icosahedron
The regular icosahedron (or simply ''icosahedron'') is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with Regular polygon, regular faces to each of its pentagonal faces, or by putting ...
, regular dodecahedron, regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
, and cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
.
Like its dual, the regular octahedron has three properties: any two faces, two vertices, and two edges are transformed by rotation and reflection under the symmetry orbit, such that the appearance remains unchanged; these are isohedral, isogonal, and isotoxal respectively. Hence, it is considered a regular polyhedron
A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In ...
. Four triangles surround each vertex, so the regular octahedron is by vertex configuration
In geometry, a vertex configuration is a shorthand notation for representing a polyhedron or Tessellation, tiling as the sequence of Face (geometry), faces around a Vertex (geometry), vertex. It has variously been called a vertex description, vert ...
or by Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
.
As a square bipyramid
 Many octahedra of interest are square bipyramids. A square bipyramid is a
Many octahedra of interest are square bipyramids. A square bipyramid is a bipyramid
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two Pyramid (geometry), pyramids together base (geometry), base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise ...
constructed by attaching two square pyramids base-to-base. These pyramids cover their square bases, so the resulting polyhedron has eight triangular faces.
A square bipyramid is said to be right if the square pyramids are symmetrically regular and both of their apices are on the line passing through the base's center; otherwise, it is oblique. The resulting bipyramid has three-dimensional point group of dihedral group
In mathematics, a dihedral group is the group (mathematics), group of symmetry, symmetries of a regular polygon, which includes rotational symmetry, rotations and reflection symmetry, reflections. Dihedral groups are among the simplest example ...
of sixteen: the appearance is symmetrical by rotating around the axis of symmetry that passing through apices and base's center vertically, and it has mirror symmetry relative to any bisector of the base; it is also symmetrical by reflecting it across a horizontal plane. Therefore, this square bipyramid is face-transitive or isohedral.
If the edges of a square bipyramid are all equal in length, then that square bipyramid is a regular octahedron.
Metric properties and Cartesian coordinates
circumscribed sphere
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's Vertex (geometry), vertices. The word circumsphere is sometimes used to mean the same thing, by analogy with the te ...
(one that touches the octahedron at all vertices), the radius of an inscribed sphere
image:Circumcentre.svg, An inscribed triangle of a circle
In geometry, an inscribed plane (geometry), planar shape or solid (geometry), solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figu ...
(one that tangent to each of the octahedron's faces), and the radius of a midsphere (one that touches the middle of each edge), are:
The dihedral angle of a regular octahedron between two adjacent triangular faces is 109.47°. This can be obtained from the dihedral angle of an equilateral square pyramid: its dihedral angle between two adjacent triangular faces is the dihedral angle of an equilateral square pyramid between two adjacent triangular faces, and its dihedral angle between two adjacent triangular faces on the edge in which two equilateral square pyramids are attached is twice the dihedral angle of an equilateral square pyramid between its triangular face and its square base.
An octahedron with edge length can be placed with its center at the origin and its vertices on the coordinate axes; the Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
of the vertices are:
Graph
skeleton
A skeleton is the structural frame that supports the body of most animals. There are several types of skeletons, including the exoskeleton, which is a rigid outer shell that holds up an organism's shape; the endoskeleton, a rigid internal fra ...
of a regular octahedron can be represented as a graph according to Steinitz's theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedron, convex polyhedra: they are exactly the vertex connect ...
, provided the graph is planar—its edges of a graph are connected to every vertex without crossing other edges—and 3-connected graph—its edges remain connected whenever two of more three vertices of a graph are removed. Its graph called the octahedral graph, a Platonic graph.
The octahedral graph can be considered as complete tripartite graph , a graph partitioned into three independent sets each consisting of two opposite vertices. More generally, it is a Turán graph .
The octahedral graph is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the pentagonal dipyramid, the snub disphenoid
In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its face (geometry), faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape is also called Siame ...
, and an irregular polyhedron with 12 vertices and 20 triangular faces.
Related figures
 The interior of the compound of two dual tetrahedra is an octahedron, and this compound—called the stella octangula—is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and
The interior of the compound of two dual tetrahedra is an octahedron, and this compound—called the stella octangula—is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron
In geometry, an icosidodecahedron or pentagonal gyrobirotunda is a polyhedron with twenty (''icosi-'') triangular faces and twelve (''dodeca-'') pentagonal faces. An icosidodecahedron has 30 identical Vertex (geometry), vertices, with two triang ...
relate to the other Platonic solids.
One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of a regular icosahedron
The regular icosahedron (or simply ''icosahedron'') is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with Regular polygon, regular faces to each of its pentagonal faces, or by putting ...
. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly partitioning each edge into the golden mean along the direction of its vector. Five octahedra define any given icosahedron in this fashion, and together they define a ''regular compound''. A regular icosahedron produced this way is called a ''snub octahedron''.
The regular octahedron can be considered as the antiprism, a prism like polyhedron in which lateral faces are replaced by alternating equilateral triangles. It is also called ''trigonal antiprism''. Therefore, it has the property of quasiregular, a polyhedron in which two different polygonal faces are alternating and meet at a vertex.
Octahedra and tetrahedra can be alternated to form a vertex, edge, and face-uniform tessellation of space. This and the regular tessellation of cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
s are the only such uniform honeycombs in 3-dimensional space.
The uniform tetrahemihexahedron is a tetrahedral symmetry
image:tetrahedron.svg, 150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry
A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that co ...
faceting of the regular octahedron, sharing edge and vertex arrangement. It has four of the triangular faces, and 3 central squares.
A regular octahedron is a 3-ball in the Manhattan () metric.
Characteristic orthoscheme
Like all regular convex polytopes, the octahedron can be dissected into an integral number of disjoint orthoschemes, all of the same shape characteristic of the polytope. A polytope's characteristic orthoscheme is a fundamental property because the polytope is generated by reflections in the facets of its orthoscheme. The orthoscheme occurs in twochiral
Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek language, Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is dist ...
forms which are mirror images of each other. The characteristic orthoscheme of a regular polyhedron is a quadrirectangular irregular tetrahedron.
The faces of the octahedron's characteristic tetrahedron lie in the octahedron's mirror planes of symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
. The octahedron is unique among the Platonic solids in having an even number of faces meeting at each vertex. Consequently, it is the only member of that group to possess, among its mirror planes, some that do not pass through any of its faces. The octahedron's symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
is denoted B3. The octahedron and its dual polytope, the cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
, have the same symmetry group but different characteristic tetrahedra.
The characteristic tetrahedron of the regular octahedron can be found by a canonical dissection of the regular octahedron which subdivides it into 48 of these characteristic orthoschemes surrounding the octahedron's center. Three left-handed orthoschemes and three right-handed orthoschemes meet in each of the octahedron's eight faces, the six orthoschemes collectively forming a trirectangular tetrahedron: a triangular pyramid with the octahedron face as its equilateral base, and its cube-cornered apex at the center of the octahedron.
If the octahedron has edge length 𝒍 = 2, its characteristic tetrahedron's six edges have lengths , , around its exterior right-triangle face (the edges opposite the ''characteristic angles'' 𝟀, 𝝉, 𝟁), plus , , (edges that are the ''characteristic radii'' of the octahedron). The 3-edge path along orthogonal edges of the orthoscheme is , , , first from an octahedron vertex to an octahedron edge center, then turning 90° to an octahedron face center, then turning 90° to the octahedron center. The orthoscheme has four dissimilar right triangle faces. The exterior face is a 90-60-30 triangle which is one-sixth of an octahedron face. The three faces interior to the octahedron are: a 45-90-45 triangle with edges , , , a right triangle with edges , , , and a right triangle with edges , , .
Uniform colorings and symmetry
There are 3 uniform colorings of the octahedron, named by the triangular face colors going around each vertex: 1212, 1112, 1111. The octahedron'ssymmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
is Oh, of order 48, the three dimensional hyperoctahedral group. This group's subgroup
In group theory, a branch of mathematics, a subset of a group G is a subgroup of G if the members of that subset form a group with respect to the group operation in G.
Formally, given a group (mathematics), group under a binary operation ...
s include D3d (order 12), the symmetry group of a triangular antiprism; D4h (order 16), the symmetry group of a square bipyramid
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two Pyramid (geometry), pyramids together base (geometry), base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise ...
; and Td (order 24), the symmetry group of a rectified tetrahedron. These symmetries can be emphasized by different colorings of the faces.
In the physical world
In nature
* Natural crystals ofdiamond
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Diamond is tasteless, odourless, strong, brittle solid, colourless in pure form, a poor conductor of e ...
, alum
An alum () is a type of chemical compound, usually a hydrated double salt, double sulfate salt (chemistry), salt of aluminium with the general chemical formula, formula , such that is a valence (chemistry), monovalent cation such as potassium ...
or fluorite are commonly octahedral, as the space-filling tetrahedral-octahedral honeycomb.
* The plates of kamacite alloy in octahedrite
Octahedrites are the most common Iron meteorite#Structural classification, structural class of iron meteorites. The structures occur because the meteoric iron has a certain nickel concentration that leads to the exsolution of kamacite out of tae ...
meteorites are arranged paralleling the eight faces of an octahedron.
* Many metal ions coordinate six ligands in an octahedral or distorted octahedral configuration.
* Widmanstätten pattern
Widmanstätten patterns (), also known as Thomson structures, are figures of long Phase (matter), phases of nickel–iron, found in the octahedrite shapes of iron meteorite crystals and some pallasites.
Iron meteorites are very often formed ...
s in nickel
Nickel is a chemical element; it has symbol Ni and atomic number 28. It is a silvery-white lustrous metal with a slight golden tinge. Nickel is a hard and ductile transition metal. Pure nickel is chemically reactive, but large pieces are slo ...
-iron
Iron is a chemical element; it has symbol Fe () and atomic number 26. It is a metal that belongs to the first transition series and group 8 of the periodic table. It is, by mass, the most common element on Earth, forming much of Earth's o ...
crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
s
In art and culture
* Especially inroleplaying game
A role-playing game (sometimes spelled roleplaying game, or abbreviated as RPG) is a game in which players assume the roles of characters in a fictional setting. Players take responsibility for acting out these roles within a narrative, eith ...
s, this solid is known as a "d8", one of the more common polyhedral dice.
* If each edge of an octahedron is replaced by a one-ohm
Ohm (symbol Ω) is a unit of electrical resistance named after Georg Ohm.
Ohm or OHM may also refer to:
People
* Georg Ohm (1789–1854), German physicist and namesake of the term ''ohm''
* Germán Ohm (born 1936), Mexican boxer
* Jörg Ohm (1 ...
resistor
A resistor is a passive two-terminal electronic component that implements electrical resistance as a circuit element. In electronic circuits, resistors are used to reduce current flow, adjust signal levels, to divide voltages, bias active e ...
, the resistance between opposite vertices is ohm, and that between adjacent vertices ohm.
* Six musical notes can be arranged on the vertices of an octahedron in such a way that each edge represents a consonant dyad and each face represents a consonant triad; see hexany.
Tetrahedral octet truss
Aspace frame
In architecture and structural engineering, a space frame or space structure (Three-dimensional space, 3D truss) is a rigid, lightweight, truss-like structure constructed from interlocking struts in a geometry, geometric pattern. Space frames can ...
of alternating tetrahedra and half-octahedra derived from the Tetrahedral-octahedral honeycomb was invented by Buckminster Fuller in the 1950s. It is commonly regarded as the strongest building structure for resisting cantilever stresses.
Tetratetrahedron
The regular octahedron can also be considered a '' rectified tetrahedron'' – and can be called a ''tetratetrahedron''. This can be shown by a 2-color face model. With this coloring, the octahedron hastetrahedral symmetry
image:tetrahedron.svg, 150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry
A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that co ...
.
Compare this truncation sequence between a tetrahedron and its dual:
The above shapes may also be realized as slices orthogonal to the long diagonal of a tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
. If this diagonal is oriented vertically with a height of 1, then the first five slices above occur at heights ''r'', , , , and ''s'', where ''r'' is any number in the range , and ''s'' is any number in the range .
The octahedron as a ''tetratetrahedron'' exists in a sequence of symmetries of quasiregular polyhedra and tilings with vertex configuration
In geometry, a vertex configuration is a shorthand notation for representing a polyhedron or Tessellation, tiling as the sequence of Face (geometry), faces around a Vertex (geometry), vertex. It has variously been called a vertex description, vert ...
s (3.''n'')2, progressing from tilings of the sphere to the Euclidean plane and into the hyperbolic plane. With orbifold notation symmetry of *''n''32 all of these tilings are Wythoff constructions within a fundamental domain
Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each ...
of symmetry, with generator points at the right angle corner of the domain.
Trigonal antiprism
As a trigonal antiprism, the octahedron is related to the hexagonal dihedral symmetry family.Other related polyhedra
Truncation of two opposite vertices results in a square bifrustum. The octahedron can be generated as the case of a 3D superellipsoid with all exponent values set to 1.See also
*Octahedral number
In number theory, an octahedral number is a figurate number that represents the number of spheres in an octahedron formed from close-packed spheres. The th octahedral number O_n can be obtained by the formula:.
:O_n=.
The first few octahedral ...
* Centered octahedral number
* Spinning octahedron
* Stella octangula
* Triakis octahedron
In geometry, a triakis octahedron (or trigonal trisoctahedron or kisoctahedronConway, Symmetries of things, p. 284) is an Archimedean solid, Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.
It can be seen as an octahedr ...
* Hexakis octahedron
* Truncated octahedron
* Octahedral molecular geometry
In chemistry, octahedral molecular geometry, also called square bipyramidal, describes the shape of compounds with six atoms or groups of atoms or ligands symmetrically arranged around a central atom, defining the vertices of an octahedron. The o ...
* Octahedral symmetry
* Octahedral graph
* Octahedral sphere
Notes
References
External links
* * *Editable printable net of an octahedron with interactive 3D view
Paper model of the octahedron
* ttp://www.mathconsult.ch/showroom/unipoly/ The Uniform Polyhedra
Virtual Reality Polyhedra
– The Encyclopedia of Polyhedra *
– Try: dP4 {{Authority control Deltahedra Individual graphs Platonic solids Prismatoid polyhedra Bipyramids