convolutional neural networks on:
[Wikipedia]
[Google]
[Amazon]
A convolutional neural network (CNN) is a type of
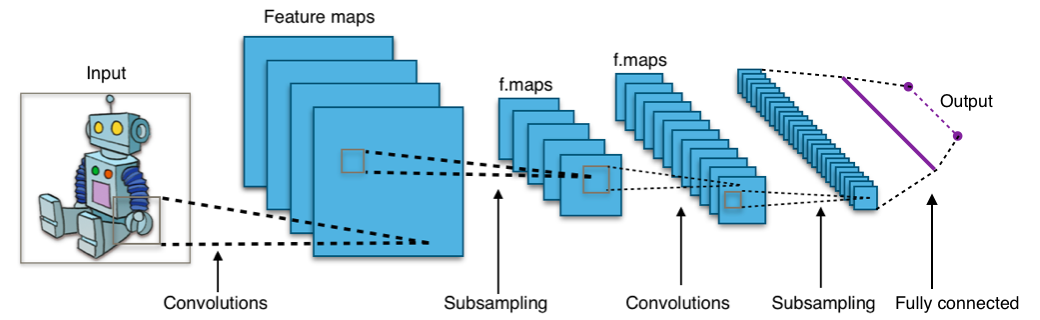
 A convolutional neural network consists of an input layer, hidden layers and an output layer. In a convolutional neural network, the hidden layers include one or more layers that perform convolutions. Typically this includes a layer that performs a
A convolutional neural network consists of an input layer, hidden layers and an output layer. In a convolutional neural network, the hidden layers include one or more layers that perform convolutions. Typically this includes a layer that performs a
 Although fully connected feedforward neural networks can be used to learn features and classify data, this architecture is generally impractical for larger inputs (e.g., high-resolution images), which would require massive numbers of neurons because each pixel is a relevant input feature. A fully connected layer for an image of size 100 × 100 has 10,000 weights for ''each'' neuron in the second layer. Convolution reduces the number of free parameters, allowing the network to be deeper. For example, using a 5 × 5 tiling region, each with the same shared weights, requires only 25 neurons. Using shared weights means there are many fewer parameters, which helps avoid the vanishing gradients and exploding gradients problems seen during backpropagation in earlier neural networks.
To speed processing, standard convolutional layers can be replaced by depthwise separable convolutional layers, which are based on a depthwise convolution followed by a pointwise convolution. The ''depthwise convolution'' is a spatial convolution applied independently over each channel of the input tensor, while the ''pointwise convolution'' is a standard convolution restricted to the use of kernels.
Although fully connected feedforward neural networks can be used to learn features and classify data, this architecture is generally impractical for larger inputs (e.g., high-resolution images), which would require massive numbers of neurons because each pixel is a relevant input feature. A fully connected layer for an image of size 100 × 100 has 10,000 weights for ''each'' neuron in the second layer. Convolution reduces the number of free parameters, allowing the network to be deeper. For example, using a 5 × 5 tiling region, each with the same shared weights, requires only 25 neurons. Using shared weights means there are many fewer parameters, which helps avoid the vanishing gradients and exploding gradients problems seen during backpropagation in earlier neural networks.
To speed processing, standard convolutional layers can be replaced by depthwise separable convolutional layers, which are based on a depthwise convolution followed by a pointwise convolution. The ''depthwise convolution'' is a spatial convolution applied independently over each channel of the input tensor, while the ''pointwise convolution'' is a standard convolution restricted to the use of kernels.
Phoneme Recognition Using Time-Delay Neural Networks
'' IEEE Transactions on Acoustics, Speech, and Signal Processing, Volume 37, No. 3, pp. 328. - 339 March 1989. Thus, while also using a pyramidal structure as in the neocognitron, it performed a global optimization of the weights instead of a local one. TDNNs are convolutional networks that share weights along the temporal dimension. They allow speech signals to be processed time-invariantly. In 1990 Hampshire and Waibel introduced a variant that performs a two-dimensional convolution.John B. Hampshire and Alexander Waibel,
Connectionist Architectures for Multi-Speaker Phoneme Recognition
'', Advances in Neural Information Processing Systems, 1990, Morgan Kaufmann. Since these TDNNs operated on spectrograms, the resulting phoneme recognition system was invariant to both time and frequency shifts, as with images processed by a neocognitron. TDNNs improved the performance of far-distance speech recognition.
Backpropagation Applied to Handwritten Zip Code Recognition
; AT&T Bell Laboratories Following the advances in the training of 1-D CNNs by Waibel et al. (1987), Yann LeCun et al. (1989) used back-propagation to learn the convolution kernel coefficients directly from images of hand-written numbers. Learning was thus fully automatic, performed better than manual coefficient design, and was suited to a broader range of image recognition problems and image types. Wei Zhang et al. (1988) used back-propagation to train the convolution kernels of a CNN for alphabets recognition. The model was called shift-invariant pattern recognition neural network before the name CNN was coined later in the early 1990s. Wei Zhang et al. also applied the same CNN without the last fully connected layer for medical image object segmentation (1991) and breast cancer detection in mammograms (1994). This approach became a foundation of modern
 For example, in CIFAR-10, images are only of size 32×32×3 (32 wide, 32 high, 3 color channels), so a single fully connected neuron in the first hidden layer of a regular neural network would have 32*32*3 = 3,072 weights. A 200×200 image, however, would lead to neurons that have 200*200*3 = 120,000 weights.
Also, such network architecture does not take into account the spatial structure of data, treating input pixels which are far apart in the same way as pixels that are close together. This ignores
For example, in CIFAR-10, images are only of size 32×32×3 (32 wide, 32 high, 3 color channels), so a single fully connected neuron in the first hidden layer of a regular neural network would have 32*32*3 = 3,072 weights. A 200×200 image, however, would lead to neurons that have 200*200*3 = 120,000 weights.
Also, such network architecture does not take into account the spatial structure of data, treating input pixels which are far apart in the same way as pixels that are close together. This ignores
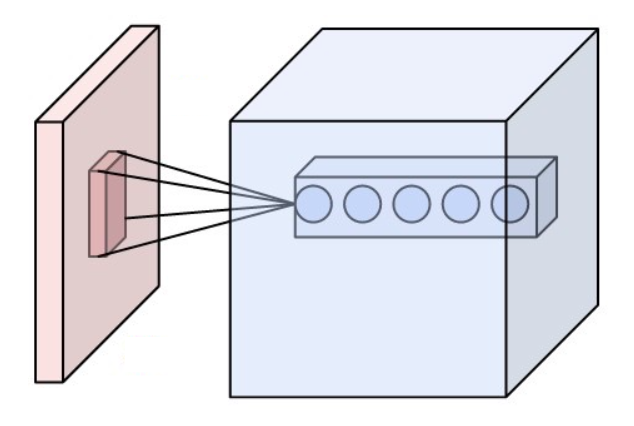
 When dealing with high-dimensional inputs such as images, it is impractical to connect neurons to all neurons in the previous volume because such a network architecture does not take the spatial structure of the data into account. Convolutional networks exploit spatially local correlation by enforcing a sparse local connectivity pattern between neurons of adjacent layers: each neuron is connected to only a small region of the input volume.
The extent of this connectivity is a hyperparameter called the receptive field of the neuron. The connections are local in space (along width and height), but always extend along the entire depth of the input volume. Such an architecture ensures that the learned filters produce the strongest response to a spatially local input pattern.
When dealing with high-dimensional inputs such as images, it is impractical to connect neurons to all neurons in the previous volume because such a network architecture does not take the spatial structure of the data into account. Convolutional networks exploit spatially local correlation by enforcing a sparse local connectivity pattern between neurons of adjacent layers: each neuron is connected to only a small region of the input volume.
The extent of this connectivity is a hyperparameter called the receptive field of the neuron. The connections are local in space (along width and height), but always extend along the entire depth of the input volume. Such an architecture ensures that the learned filters produce the strongest response to a spatially local input pattern.

feedforward neural network
Feedforward refers to recognition-inference architecture of neural networks. Artificial neural network architectures are based on inputs multiplied by weights to obtain outputs (inputs-to-output): feedforward. Recurrent neural networks, or neur ...
that learns features via filter (or kernel) optimization. This type of deep learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience a ...
network has been applied to process and make predictions from many different types of data including text, images and audio. Convolution-based networks are the de-facto standard in deep learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience a ...
-based approaches to computer vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical ...
and image processing, and have only recently been replaced—in some cases—by newer deep learning architectures such as the transformer
In electrical engineering, a transformer is a passive component that transfers electrical energy from one electrical circuit to another circuit, or multiple Electrical network, circuits. A varying current in any coil of the transformer produces ...
.
Vanishing gradients and exploding gradients, seen during backpropagation in earlier neural networks, are prevented by the regularization that comes from using shared weights over fewer connections. For example, for ''each'' neuron in the fully-connected layer, 10,000 weights would be required for processing an image sized 100 × 100 pixels. However, applying cascaded ''convolution'' (or cross-correlation) kernels, only 25 weights for each convolutional layer are required to process 5x5-sized tiles. Higher-layer features are extracted from wider context windows, compared to lower-layer features.
Some applications of CNNs include:
* image and video recognition,
* recommender system
A recommender system (RecSys), or a recommendation system (sometimes replacing ''system'' with terms such as ''platform'', ''engine'', or ''algorithm'') and sometimes only called "the algorithm" or "algorithm", is a subclass of information fi ...
s,
* image classification,
* image segmentation,
* medical image analysis
Medical image computing (MIC) is an interdisciplinary field at the intersection of computer science, information engineering, electrical engineering, physics, mathematics and medicine. This field develops computational and mathematical methods fo ...
,
* natural language processing
Natural language processing (NLP) is a subfield of computer science and especially artificial intelligence. It is primarily concerned with providing computers with the ability to process data encoded in natural language and is thus closely related ...
,
* brain–computer interface
A brain–computer interface (BCI), sometimes called a brain–machine interface (BMI), is a direct communication link between the brain's electrical activity and an external device, most commonly a computer or robotic limb. BCIs are often dire ...
s, and
* financial time series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. ...
.
CNNs are also known as shift invariant or space invariant artificial neural networks, based on the shared-weight architecture of the convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
kernels or filters that slide along input features and provide translation- equivariant responses known as feature maps. Counter-intuitively, most convolutional neural networks are not invariant to translation, due to the downsampling operation they apply to the input.
Feedforward neural network
Feedforward refers to recognition-inference architecture of neural networks. Artificial neural network architectures are based on inputs multiplied by weights to obtain outputs (inputs-to-output): feedforward. Recurrent neural networks, or neur ...
s are usually fully connected networks, that is, each neuron in one layer is connected to all neurons in the next layer. The "full connectivity" of these networks makes them prone to overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfi ...
data. Typical ways of regularization, or preventing overfitting, include: penalizing parameters during training (such as weight decay) or trimming connectivity (skipped connections, dropout, etc.) Robust datasets also increase the probability that CNNs will learn the generalized principles that characterize a given dataset rather than the biases of a poorly-populated set.
Convolutional networks were inspired by biological processes in that the connectivity pattern between neurons
A neuron (American English), neurone (British English), or nerve cell, is an membrane potential#Cell excitability, excitable cell (biology), cell that fires electric signals called action potentials across a neural network (biology), neural net ...
resembles the organization of the animal visual cortex
The visual cortex of the brain is the area of the cerebral cortex that processes visual information. It is located in the occipital lobe. Sensory input originating from the eyes travels through the lateral geniculate nucleus in the thalam ...
. Individual cortical neurons respond to stimuli only in a restricted region of the visual field known as the receptive field. The receptive fields of different neurons partially overlap such that they cover the entire visual field.
CNNs use relatively little pre-processing compared to other image classification algorithms. This means that the network learns to optimize the filters
Filtration is a physical process that separates solid matter and fluid from a mixture.
Filter, filtering, filters or filtration may also refer to:
Science and technology
Computing
* Filter (higher-order function), in functional programming
* Fil ...
(or kernels) through automated learning, whereas in traditional algorithms these filters are hand-engineered. This simplifies and automates the process, enhancing efficiency and scalability overcoming human-intervention bottlenecks.
Architecture
dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
of the convolution kernel with the layer's input matrix. This product is usually the Frobenius inner product, and its activation function is commonly ReLU. As the convolution kernel slides along the input matrix for the layer, the convolution operation generates a feature map, which in turn contributes to the input of the next layer. This is followed by other layers such as pooling layers, fully connected layers, and normalization layers.
Here it should be noted how close a convolutional neural network is to a matched filter.
Convolutional layers
In a CNN, the input is atensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
with shape:
(number of inputs) × (input height) × (input width) × (input channels)
After passing through a convolutional layer, the image becomes abstracted to a feature map, also called an activation map, with shape:
(number of inputs) × (feature map height) × (feature map width) × (feature map channels).
Convolutional layers convolve the input and pass its result to the next layer. This is similar to the response of a neuron in the visual cortex to a specific stimulus. Each convolutional neuron processes data only for its receptive field.
 Although fully connected feedforward neural networks can be used to learn features and classify data, this architecture is generally impractical for larger inputs (e.g., high-resolution images), which would require massive numbers of neurons because each pixel is a relevant input feature. A fully connected layer for an image of size 100 × 100 has 10,000 weights for ''each'' neuron in the second layer. Convolution reduces the number of free parameters, allowing the network to be deeper. For example, using a 5 × 5 tiling region, each with the same shared weights, requires only 25 neurons. Using shared weights means there are many fewer parameters, which helps avoid the vanishing gradients and exploding gradients problems seen during backpropagation in earlier neural networks.
To speed processing, standard convolutional layers can be replaced by depthwise separable convolutional layers, which are based on a depthwise convolution followed by a pointwise convolution. The ''depthwise convolution'' is a spatial convolution applied independently over each channel of the input tensor, while the ''pointwise convolution'' is a standard convolution restricted to the use of kernels.
Although fully connected feedforward neural networks can be used to learn features and classify data, this architecture is generally impractical for larger inputs (e.g., high-resolution images), which would require massive numbers of neurons because each pixel is a relevant input feature. A fully connected layer for an image of size 100 × 100 has 10,000 weights for ''each'' neuron in the second layer. Convolution reduces the number of free parameters, allowing the network to be deeper. For example, using a 5 × 5 tiling region, each with the same shared weights, requires only 25 neurons. Using shared weights means there are many fewer parameters, which helps avoid the vanishing gradients and exploding gradients problems seen during backpropagation in earlier neural networks.
To speed processing, standard convolutional layers can be replaced by depthwise separable convolutional layers, which are based on a depthwise convolution followed by a pointwise convolution. The ''depthwise convolution'' is a spatial convolution applied independently over each channel of the input tensor, while the ''pointwise convolution'' is a standard convolution restricted to the use of kernels.
Pooling layers
Convolutional networks may include local and/or global pooling layers along with traditional convolutional layers. Pooling layers reduce the dimensions of data by combining the outputs of neuron clusters at one layer into a single neuron in the next layer. Local pooling combines small clusters, tiling sizes such as 2 × 2 are commonly used. Global pooling acts on all the neurons of the feature map. There are two common types of pooling in popular use: max and average. ''Max pooling'' uses the maximum value of each local cluster of neurons in the feature map, while ''average pooling'' takes the average value.Fully connected layers
Fully connected layers connect every neuron in one layer to every neuron in another layer. It is the same as a traditional multilayer perceptron neural network (MLP). The flattened matrix goes through a fully connected layer to classify the images.Receptive field
In neural networks, each neuron receives input from some number of locations in the previous layer. In a convolutional layer, each neuron receives input from only a restricted area of the previous layer called the neuron's ''receptive field''. Typically the area is a square (e.g. 5 by 5 neurons). Whereas, in a fully connected layer, the receptive field is the ''entire previous layer''. Thus, in each convolutional layer, each neuron takes input from a larger area in the input than previous layers. This is due to applying the convolution over and over, which takes the value of a pixel into account, as well as its surrounding pixels. When using dilated layers, the number of pixels in the receptive field remains constant, but the field is more sparsely populated as its dimensions grow when combining the effect of several layers. To manipulate the receptive field size as desired, there are some alternatives to the standard convolutional layer. For example, atrous or dilated convolution expands the receptive field size without increasing the number of parameters by interleaving visible and blind regions. Moreover, a single dilated convolutional layer can comprise filters with multiple dilation ratios, thus having a variable receptive field size.Weights
Each neuron in a neural network computes an output value by applying a specific function to the input values received from the receptive field in the previous layer. The function that is applied to the input values is determined by a vector of weights and a bias (typically real numbers). Learning consists of iteratively adjusting these biases and weights. The vectors of weights and biases are called ''filters'' and represent particularfeature
Feature may refer to:
Computing
* Feature recognition, could be a hole, pocket, or notch
* Feature (computer vision), could be an edge, corner or blob
* Feature (machine learning), in statistics: individual measurable properties of the phenome ...
s of the input (e.g., a particular shape). A distinguishing feature of CNNs is that many neurons can share the same filter. This reduces the memory footprint
Memory footprint refers to the amount of main memory that a program uses or references while running.
The word footprint generally refers to the extent of physical dimensions that an object occupies, giving a sense of its size. In computing, t ...
because a single bias and a single vector of weights are used across all receptive fields that share that filter, as opposed to each receptive field having its own bias and vector weighting.
Deconvolutional
A deconvolutional neural network is essentially the reverse of a CNN. It consists of deconvolutional layers and unpooling layers. A deconvolutional layer is the transpose of a convolutional layer. Specifically, a convolutional layer can be written as a multiplication with a matrix, and a deconvolutional layer is multiplication with the transpose of that matrix. An unpooling layer expands the layer. The max-unpooling layer is the simplest, as it simply copies each entry multiple times. For example, a 2-by-2 max-unpooling layer is . Deconvolution layers are used in image generators. By default, it creates periodic checkerboard artifact, which can be fixed by upscale-then-convolve.History
CNN are often compared to the way the brain achieves vision processing in livingorganisms
An organism is any living thing that functions as an individual. Such a definition raises more problems than it solves, not least because the concept of an individual is also difficult. Many criteria, few of them widely accepted, have been pr ...
.
Receptive fields in the visual cortex
Work by Hubel and Wiesel in the 1950s and 1960s showed that cat visual cortices contain neurons that individually respond to small regions of the visual field. Provided the eyes are not moving, the region of visual space within which visual stimuli affect the firing of a single neuron is known as its receptive field. Neighboring cells have similar and overlapping receptive fields. Receptive field size and location varies systematically across the cortex to form a complete map of visual space. The cortex in each hemisphere represents the contralateral visual field. Their 1968 paper identified two basic visual cell types in the brain: * simple cells, whose output is maximized by straight edges having particular orientations within their receptive field * complex cells, which have larger receptive fields, whose output is insensitive to the exact position of the edges in the field. Hubel and Wiesel also proposed a cascading model of these two types of cells for use in pattern recognition tasks.Fukushima's analog threshold elements in a vision model
In 1969, Kunihiko Fukushima introduced a multilayer visual feature detection network, inspired by the above-mentioned work of Hubel and Wiesel, in which "All the elements in one layer have the same set of interconnecting coefficients; the arrangement of the elements and their interconnections are all homogeneous over a given layer." This is the essential core of a convolutional network, but the weights were not trained. In the same paper, Fukushima also introduced the ReLU (rectified linear unit) activation function.Neocognitron, origin of the trainable CNN architecture
The " neocognitron" was introduced by Fukushima in 1980. The neocognitron introduced the two basic types of layers: * "S-layer": a shared-weights receptive-field layer, later known as a convolutional layer, which contains units whose receptive fields cover a patch of the previous layer. A shared-weights receptive-field group (a "plane" in neocognitron terminology) is often called a filter, and a layer typically has several such filters. * "C-layer": a downsampling layer that contain units whose receptive fields cover patches of previous convolutional layers. Such a unit typically computes a weighted average of the activations of the units in its patch, and applies inhibition (divisive normalization) pooled from a somewhat larger patch and across different filters in a layer, and applies a saturating activation function. The patch weights are nonnegative and are not trainable in the original neocognitron. The downsampling and competitive inhibition help to classify features and objects in visual scenes even when the objects are shifted. Several supervised and unsupervised learning algorithms have been proposed over the decades to train the weights of a neocognitron. Today, however, the CNN architecture is usually trained through backpropagation. Fukushima's ReLU activation function was not used in his neocognitron since all the weights were nonnegative; lateral inhibition was used instead. The rectifier has become a very popular activation function for CNNs and deep neural networks in general.Convolution in time
The term "convolution" first appears in neural networks in a paper by Toshiteru Homma, Les Atlas, and Robert Marks II at the first Conference on Neural Information Processing Systems in 1987. Their paper replaced multiplication with convolution in time, inherently providing shift invariance, motivated by and connecting more directly to the signal-processing concept of a filter, and demonstrated it on a speech recognition task. They also pointed out that as a data-trainable system, convolution is essentially equivalent to correlation since reversal of the weights does not affect the final learned function ("For convenience, we denote * as correlation instead of convolution. Note that convolving a(t) with b(t) is equivalent to correlating a(-t) with b(t)."). Modern CNN implementations typically do correlation and call it convolution, for convenience, as they did here.Time delay neural networks
The time delay neural network (TDNN) was introduced in 1987 by Alex Waibel et al. for phoneme recognition and was an early convolutional network exhibiting shift-invariance. A TDNN is a 1-D convolutional neural net where the convolution is performed along the time axis of the data. It is the first CNN utilizing weight sharing in combination with a training by gradient descent, using backpropagation. Alexander Waibel et al.,Phoneme Recognition Using Time-Delay Neural Networks
'' IEEE Transactions on Acoustics, Speech, and Signal Processing, Volume 37, No. 3, pp. 328. - 339 March 1989. Thus, while also using a pyramidal structure as in the neocognitron, it performed a global optimization of the weights instead of a local one. TDNNs are convolutional networks that share weights along the temporal dimension. They allow speech signals to be processed time-invariantly. In 1990 Hampshire and Waibel introduced a variant that performs a two-dimensional convolution.John B. Hampshire and Alexander Waibel,
Connectionist Architectures for Multi-Speaker Phoneme Recognition
'', Advances in Neural Information Processing Systems, 1990, Morgan Kaufmann. Since these TDNNs operated on spectrograms, the resulting phoneme recognition system was invariant to both time and frequency shifts, as with images processed by a neocognitron. TDNNs improved the performance of far-distance speech recognition.
Image recognition with CNNs trained by gradient descent
Denker et al. (1989) designed a 2-D CNN system to recognize hand-written ZIP Code numbers. However, the lack of an efficient training method to determine the kernel coefficients of the involved convolutions meant that all the coefficients had to be laboriously hand-designed.Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, L. D. JackelBackpropagation Applied to Handwritten Zip Code Recognition
; AT&T Bell Laboratories Following the advances in the training of 1-D CNNs by Waibel et al. (1987), Yann LeCun et al. (1989) used back-propagation to learn the convolution kernel coefficients directly from images of hand-written numbers. Learning was thus fully automatic, performed better than manual coefficient design, and was suited to a broader range of image recognition problems and image types. Wei Zhang et al. (1988) used back-propagation to train the convolution kernels of a CNN for alphabets recognition. The model was called shift-invariant pattern recognition neural network before the name CNN was coined later in the early 1990s. Wei Zhang et al. also applied the same CNN without the last fully connected layer for medical image object segmentation (1991) and breast cancer detection in mammograms (1994). This approach became a foundation of modern
computer vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical ...
.
Max pooling
In 1990 Yamaguchi et al. introduced the concept of max pooling, a fixed filtering operation that calculates and propagates the maximum value of a given region. They did so by combining TDNNs with max pooling to realize a speaker-independent isolated word recognition system. In their system they used several TDNNs per word, one for eachsyllable
A syllable is a basic unit of organization within a sequence of speech sounds, such as within a word, typically defined by linguists as a ''nucleus'' (most often a vowel) with optional sounds before or after that nucleus (''margins'', which are ...
. The results of each TDNN over the input signal were combined using max pooling and the outputs of the pooling layers were then passed on to networks performing the actual word classification.
In a variant of the neocognitron called the ''cresceptron'', instead of using Fukushima's spatial averaging with inhibition and saturation, J. Weng et al. in 1993 used max pooling, where a downsampling unit computes the maximum of the activations of the units in its patch, introducing this method into the vision field.
Max pooling is often used in modern CNNs.
LeNet-5
LeNet-5, a pioneering 7-level convolutional network by LeCun et al. in 1995, classifies hand-written numbers on checks () digitized in 32x32 pixel images. The ability to process higher-resolution images requires larger and more layers of convolutional neural networks, so this technique is constrained by the availability of computing resources. It was superior than other commercial courtesy amount reading systems (as of 1995). The system was integrated in NCR's check reading systems, and fielded in several American banks since June 1996, reading millions of checks per day.Shift-invariant neural network
A shift-invariant neural network was proposed by Wei Zhang et al. for image character recognition in 1988. It is a modified Neocognitron by keeping only the convolutional interconnections between the image feature layers and the last fully connected layer. The model was trained with back-propagation. The training algorithm was further improved in 1991 to improve its generalization ability. The model architecture was modified by removing the last fully connected layer and applied for medical image segmentation (1991) and automatic detection of breast cancer in mammograms (1994). A different convolution-based design was proposed in 1988 for application to decomposition of one-dimensionalelectromyography
Electromyography (EMG) is a technique for evaluating and recording the electrical activity produced by skeletal muscles. EMG is performed using an instrument called an electromyograph to produce a record called an electromyogram. An electromyo ...
convolved signals via de-convolution. This design was modified in 1989 to other de-convolution-based designs.
GPU implementations
Although CNNs were invented in the 1980s, their breakthrough in the 2000s required fast implementations ongraphics processing unit
A graphics processing unit (GPU) is a specialized electronic circuit designed for digital image processing and to accelerate computer graphics, being present either as a discrete video card or embedded on motherboards, mobile phones, personal ...
s (GPUs).
In 2004, it was shown by K. S. Oh and K. Jung that standard neural networks can be greatly accelerated on GPUs. Their implementation was 20 times faster than an equivalent implementation on CPU. In 2005, another paper also emphasised the value of GPGPU
General-purpose computing on graphics processing units (GPGPU, or less often GPGP) is the use of a graphics processing unit (GPU), which typically handles computation only for computer graphics, to perform computation in applications traditiona ...
for machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
.
The first GPU-implementation of a CNN was described in 2006 by K. Chellapilla et al. Their implementation was 4 times faster than an equivalent implementation on CPU. In the same period, GPUs were also used for unsupervised training of deep belief networks.
In 2010, Dan Ciresan et al. at IDSIA trained deep feedforward networks on GPUs. In 2011, they extended this to CNNs, accelerating by 60 compared to training CPU. In 2011, the network won an image recognition contest where they achieved superhuman performance for the first time. Then they won more competitions and achieved state of the art on several benchmarks.
Subsequently, AlexNet, a similar GPU-based CNN by Alex Krizhevsky et al. won the ImageNet Large Scale Visual Recognition Challenge 2012. It was an early catalytic event for the AI boom.
Compared to the training of CNNs using GPUs, not much attention was given to CPU. (Viebke et al 2019) parallelizes CNN by thread- and SIMD
Single instruction, multiple data (SIMD) is a type of parallel computer, parallel processing in Flynn's taxonomy. SIMD describes computers with multiple processing elements that perform the same operation on multiple data points simultaneousl ...
-level parallelism that is available on the Intel Xeon Phi.
Distinguishing features
In the past, traditional multilayer perceptron (MLP) models were used for image recognition. However, the full connectivity between nodes caused the curse of dimensionality, and was computationally intractable with higher-resolution images. A 1000×1000-pixel image with RGB color channels has 3 million weights per fully-connected neuron, which is too high to feasibly process efficiently at scale. For example, in CIFAR-10, images are only of size 32×32×3 (32 wide, 32 high, 3 color channels), so a single fully connected neuron in the first hidden layer of a regular neural network would have 32*32*3 = 3,072 weights. A 200×200 image, however, would lead to neurons that have 200*200*3 = 120,000 weights.
Also, such network architecture does not take into account the spatial structure of data, treating input pixels which are far apart in the same way as pixels that are close together. This ignores
For example, in CIFAR-10, images are only of size 32×32×3 (32 wide, 32 high, 3 color channels), so a single fully connected neuron in the first hidden layer of a regular neural network would have 32*32*3 = 3,072 weights. A 200×200 image, however, would lead to neurons that have 200*200*3 = 120,000 weights.
Also, such network architecture does not take into account the spatial structure of data, treating input pixels which are far apart in the same way as pixels that are close together. This ignores locality of reference
In computer science, locality of reference, also known as the principle of locality, is the tendency of a processor to access the same set of memory locations repetitively over a short period of time. There are two basic types of reference localit ...
in data with a grid-topology (such as images), both computationally and semantically. Thus, full connectivity of neurons is wasteful for purposes such as image recognition that are dominated by spatially local input patterns.
Convolutional neural networks are variants of multilayer perceptrons, designed to emulate the behavior of a visual cortex
The visual cortex of the brain is the area of the cerebral cortex that processes visual information. It is located in the occipital lobe. Sensory input originating from the eyes travels through the lateral geniculate nucleus in the thalam ...
. These models mitigate the challenges posed by the MLP architecture by exploiting the strong spatially local correlation present in natural images. As opposed to MLPs, CNNs have the following distinguishing features:
* 3D volumes of neurons. The layers of a CNN have neurons arranged in 3 dimensions: width, height and depth. Where each neuron inside a convolutional layer is connected to only a small region of the layer before it, called a receptive field. Distinct types of layers, both locally and completely connected, are stacked to form a CNN architecture.
* Local connectivity: following the concept of receptive fields, CNNs exploit spatial locality by enforcing a local connectivity pattern between neurons of adjacent layers. The architecture thus ensures that the learned "filters
Filtration is a physical process that separates solid matter and fluid from a mixture.
Filter, filtering, filters or filtration may also refer to:
Science and technology
Computing
* Filter (higher-order function), in functional programming
* Fil ...
" produce the strongest response to a spatially local input pattern. Stacking many such layers leads to nonlinear filters that become increasingly global (i.e. responsive to a larger region of pixel space) so that the network first creates representations of small parts of the input, then from them assembles representations of larger areas.
* Shared weights: In CNNs, each filter is replicated across the entire visual field. These replicated units share the same parameterization (weight vector and bias) and form a feature map. This means that all the neurons in a given convolutional layer respond to the same feature within their specific response field. Replicating units in this way allows for the resulting activation map to be equivariant under shifts of the locations of input features in the visual field, i.e. they grant translational equivariance—given that the layer has a stride of one.
* Pooling: In a CNN's pooling layers, feature maps are divided into rectangular sub-regions, and the features in each rectangle are independently down-sampled to a single value, commonly by taking their average or maximum value. In addition to reducing the sizes of feature maps, the pooling operation grants a degree of local translational invariance to the features contained therein, allowing the CNN to be more robust to variations in their positions.
Together, these properties allow CNNs to achieve better generalization on vision problems. Weight sharing dramatically reduces the number of free parameters learned, thus lowering the memory requirements for running the network and allowing the training of larger, more powerful networks.
Building blocks
A CNN architecture is formed by a stack of distinct layers that transform the input volume into an output volume (e.g. holding the class scores) through a differentiable function. A few distinct types of layers are commonly used. These are further discussed below.
Convolutional layer
The convolutional layer is the core building block of a CNN. The layer's parameters consist of a set of learnablefilters
Filtration is a physical process that separates solid matter and fluid from a mixture.
Filter, filtering, filters or filtration may also refer to:
Science and technology
Computing
* Filter (higher-order function), in functional programming
* Fil ...
(or kernels), which have a small receptive field, but extend through the full depth of the input volume. During the forward pass, each filter is convolved across the width and height of the input volume, computing the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
between the filter entries and the input, producing a 2-dimensional activation map of that filter. As a result, the network learns filters that activate when it detects some specific type of feature
Feature may refer to:
Computing
* Feature recognition, could be a hole, pocket, or notch
* Feature (computer vision), could be an edge, corner or blob
* Feature (machine learning), in statistics: individual measurable properties of the phenome ...
at some spatial position in the input., pp. 448When applied to other types of data than image data, such as sound data, "spatial position" may variously correspond to different points in the time domain
In mathematics and signal processing, the time domain is a representation of how a signal, function, or data set varies with time. It is used for the analysis of mathematical functions, physical signals or time series of economic or environmental ...
, frequency domain
In mathematics, physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency (and possibly phase), rather than time, as in time ser ...
, or other mathematical spaces
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include num ...
.
Stacking the activation maps for all filters along the depth dimension forms the full output volume of the convolution layer. Every entry in the output volume can thus also be interpreted as an output of a neuron that looks at a small region in the input. Each entry in an activation map use the same set of parameters that define the filter.
Self-supervised learning has been adapted for use in convolutional layers by using sparse patches with a high-mask ratio and a global response normalization layer.
Local connectivity
 When dealing with high-dimensional inputs such as images, it is impractical to connect neurons to all neurons in the previous volume because such a network architecture does not take the spatial structure of the data into account. Convolutional networks exploit spatially local correlation by enforcing a sparse local connectivity pattern between neurons of adjacent layers: each neuron is connected to only a small region of the input volume.
The extent of this connectivity is a hyperparameter called the receptive field of the neuron. The connections are local in space (along width and height), but always extend along the entire depth of the input volume. Such an architecture ensures that the learned filters produce the strongest response to a spatially local input pattern.
When dealing with high-dimensional inputs such as images, it is impractical to connect neurons to all neurons in the previous volume because such a network architecture does not take the spatial structure of the data into account. Convolutional networks exploit spatially local correlation by enforcing a sparse local connectivity pattern between neurons of adjacent layers: each neuron is connected to only a small region of the input volume.
The extent of this connectivity is a hyperparameter called the receptive field of the neuron. The connections are local in space (along width and height), but always extend along the entire depth of the input volume. Such an architecture ensures that the learned filters produce the strongest response to a spatially local input pattern.
Spatial arrangement
Three hyperparameters control the size of the output volume of the convolutional layer: the depth, stride, and padding size: * The ''depth'' of the output volume controls the number of neurons in a layer that connect to the same region of the input volume. These neurons learn to activate for different features in the input. For example, if the first convolutional layer takes the raw image as input, then different neurons along the depth dimension may activate in the presence of various oriented edges, or blobs of color. *''Stride'' controls how depth columns around the width and height are allocated. If the stride is 1, then we move the filters one pixel at a time. This leads to heavily overlapping receptive fields between the columns, and to large output volumes. For any integer a stride ''S'' means that the filter is translated ''S'' units at a time per output. In practice, is rare. A greater stride means smaller overlap of receptive fields and smaller spatial dimensions of the output volume. * Sometimes, it is convenient to pad the input with zeros (or other values, such as the average of the region) on the border of the input volume. The size of this padding is a third hyperparameter. Padding provides control of the output volume's spatial size. In particular, sometimes it is desirable to exactly preserve the spatial size of the input volume, this is commonly referred to as "same" padding. The spatial size of the output volume is a function of the input volume size , the kernel field size of the convolutional layer neurons, the stride , and the amount of zero padding on the border. The number of neurons that "fit" in a given volume is then: : If this number is not aninteger
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
, then the strides are incorrect and the neurons cannot be tiled to fit across the input volume in a symmetric way. In general, setting zero padding to be when the stride is ensures that the input volume and output volume will have the same size spatially. However, it is not always completely necessary to use all of the neurons of the previous layer. For example, a neural network designer may decide to use just a portion of padding.
Parameter sharing
A parameter sharing scheme is used in convolutional layers to control the number of free parameters. It relies on the assumption that if a patch feature is useful to compute at some spatial position, then it should also be useful to compute at other positions. Denoting a single 2-dimensional slice of depth as a ''depth slice'', the neurons in each depth slice are constrained to use the same weights and bias. Since all neurons in a single depth slice share the same parameters, the forward pass in each depth slice of the convolutional layer can be computed as aconvolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
of the neuron's weights with the input volume.hence the name "convolutional layer" Therefore, it is common to refer to the sets of weights as a filter (or a kernel), which is convolved with the input. The result of this convolution is an activation map, and the set of activation maps for each different filter are stacked together along the depth dimension to produce the output volume. Parameter sharing contributes to the translation invariance
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation (without rotation). Discrete translational symmetry is invariant under discrete translation.
Analogously, an opera ...
of the CNN architecture.
Sometimes, the parameter sharing assumption may not make sense. This is especially the case when the input images to a CNN have some specific centered structure; for which we expect completely different features to be learned on different spatial locations. One practical example is when the inputs are faces that have been centered in the image: we might expect different eye-specific or hair-specific features to be learned in different parts of the image. In that case it is common to relax the parameter sharing scheme, and instead simply call the layer a "locally connected layer".
Pooling layer
Another important concept of CNNs is pooling, which is used as a form of non-linear down-sampling. Pooling provides downsampling because it reduces the spatial dimensions (height and width) of the input feature maps while retaining the most important information. There are several non-linear functions to implement pooling, where ''max pooling'' and ''average pooling'' are the most common. Pooling aggregates information from small regions of the input creating partitions of the input feature map, typically using a fixed-size window (like 2x2) and applying a stride (often 2) to move the window across the input. Note that without using a stride greater than 1, pooling would not perform downsampling, as it would simply move the pooling window across the input one step at a time, without reducing the size of the feature map. In other words, the stride is what actually causes the downsampling by determining how much the pooling window moves over the input. Intuitively, the exact location of a feature is less important than its rough location relative to other features. This is the idea behind the use of pooling in convolutional neural networks. The pooling layer serves to progressively reduce the spatial size of the representation, to reduce the number of parameters,memory footprint
Memory footprint refers to the amount of main memory that a program uses or references while running.
The word footprint generally refers to the extent of physical dimensions that an object occupies, giving a sense of its size. In computing, t ...
and amount of computation in the network, and hence to also control overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfi ...
. This is known as down-sampling. It is common to periodically insert a pooling layer between successive convolutional layers (each one typically followed by an activation function, such as a ReLU layer) in a CNN architecture. While pooling layers contribute to local translation invariance, they do not provide global translation invariance in a CNN, unless a form of global pooling is used. The pooling layer commonly operates independently on every depth, or slice, of the input and resizes it spatially. A very common form of max pooling is a layer with filters of size 2×2, applied with a stride of 2, which subsamples every depth slice in the input by 2 along both width and height, discarding 75% of the activations:
In this case, every max operation is over 4 numbers. The depth dimension remains unchanged (this is true for other forms of pooling as well).
In addition to max pooling, pooling units can use other functions, such as average
In colloquial, ordinary language, an average is a single number or value that best represents a set of data. The type of average taken as most typically representative of a list of numbers is the arithmetic mean the sum of the numbers divided by ...
pooling or ℓ2-norm pooling. Average pooling was often used historically but has recently fallen out of favor compared to max pooling, which generally performs better in practice.
Due to the effects of fast spatial reduction of the size of the representation, there is a recent trend towards using smaller filters or discarding pooling layers altogether.

Channel max pooling
A channel max pooling (CMP) operation layer conducts the MP operation along the channel side among the corresponding positions of the consecutive feature maps for the purpose of redundant information elimination. The CMP makes the significant features gather together within fewer channels, which is important for fine-grained image classification that needs more discriminating features. Meanwhile, another advantage of the CMP operation is to make the channel number of feature maps smaller before it connects to the first fully connected (FC) layer. Similar to the MP operation, we denote the input feature maps and output feature maps of a CMP layer as F ∈ R(C×M×N) and C ∈ R(c×M×N), respectively, where C and c are the channel numbers of the input and output feature maps, M and N are the widths and the height of the feature maps, respectively. Note that the CMP operation only changes the channel number of the feature maps. The width and the height of the feature maps are not changed, which is different from the MP operation. See for reviews for pooling methods.ReLU layer
ReLU is the abbreviation of rectified linear unit. It was proposed by Alston Householder in 1941, and used in CNN by Kunihiko Fukushima in 1969. ReLU applies the non-saturating activation function . It effectively removes negative values from an activation map by setting them to zero. It introducesnonlinearity
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
to the decision function and in the overall network without affecting the receptive fields of the convolution layers.
In 2011, Xavier Glorot, Antoine Bordes and Yoshua Bengio found that ReLU enables better training of deeper networks, compared to widely used activation functions prior to 2011.
Other functions can also be used to increase nonlinearity, for example the saturating hyperbolic tangent , , and the sigmoid function
A sigmoid function is any mathematical function whose graph of a function, graph has a characteristic S-shaped or sigmoid curve.
A common example of a sigmoid function is the logistic function, which is defined by the formula
:\sigma(x ...
. ReLU is often preferred to other functions because it trains the neural network several times faster without a significant penalty to generalization
A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteri ...
accuracy.
Fully connected layer
After several convolutional and max pooling layers, the final classification is done via fully connected layers. Neurons in a fully connected layer have connections to all activations in the previous layer, as seen in regular (non-convolutional)artificial neural network
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
s. Their activations can thus be computed as an affine transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, '' affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
More general ...
, with matrix multiplication
In mathematics, specifically in linear algebra, matrix multiplication is a binary operation that produces a matrix (mathematics), matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the n ...
followed by a bias offset (vector addition
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
of a learned or fixed bias term).
Loss layer
The "loss layer", or " loss function", exemplifies howtraining
Training is teaching, or developing in oneself or others, any skills and knowledge or fitness that relate to specific useful competencies. Training has specific goals of improving one's capability, capacity, productivity and performance. I ...
penalizes the deviation between the predicted output of the network, and the true
True most commonly refers to truth, the state of being in congruence with fact or reality.
True may also refer to:
Places
* True, West Virginia, an unincorporated community in the United States
* True, Wisconsin, a town in the United States
* ...
data labels (during supervised learning). Various loss functions can be used, depending on the specific task.
The Softmax loss function is used for predicting a single class of ''K'' mutually exclusive classes.So-called categorical data. Sigmoid cross-entropy loss is used for predicting ''K'' independent probability values in